|
|
|
|
@ -113,6 +113,60 @@ signed main() {
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
## 树的直径
|
|
|
|
|
|
|
|
|
|
#### [$AcWing$ $1072$ 树的最长路径](https://www.cnblogs.com/littlehb/p/15784687.html)
|
|
|
|
|
|
|
|
|
|
**$Code$**
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
|
|
|
|
using namespace std;
|
|
|
|
|
const int N = 10010, M = N << 1;
|
|
|
|
|
int n; // n个结点
|
|
|
|
|
|
|
|
|
|
// 链式前向星
|
|
|
|
|
int h[N], e[M], w[M], ne[M], idx;
|
|
|
|
|
void add(int a, int b, int c) {
|
|
|
|
|
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
// 换根dp模板
|
|
|
|
|
int ans; // 答案,直径
|
|
|
|
|
int d1[N], d2[N]; // d1[i],d2[i]:经过i点的最长,次长长度是多少
|
|
|
|
|
bool st[N]; // 是不是遍历过了
|
|
|
|
|
void dfs(int u) {
|
|
|
|
|
st[u] = true;
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
int v = e[i];
|
|
|
|
|
if (st[v]) continue; // v点访问过了
|
|
|
|
|
|
|
|
|
|
// 走v子树,完成后,v子树中每个节点的d1[v],d2[v]都已经准备好,u节点可以直接利用
|
|
|
|
|
dfs(v);
|
|
|
|
|
|
|
|
|
|
// w[i]:u->v的路径长度,d1[u]:最长路径,d2[u]:次长路径
|
|
|
|
|
if (d1[v] + w[i] >= d1[u]) // v可以用来更新u的最大值
|
|
|
|
|
d2[u] = d1[u], d1[u] = d1[v] + w[i]; // 最长路转移
|
|
|
|
|
else if (d1[v] + w[i] > d2[u])
|
|
|
|
|
d2[u] = d1[v] + w[i]; // 次长路转移
|
|
|
|
|
}
|
|
|
|
|
// 更新结果
|
|
|
|
|
ans = max(ans, d1[u] + d2[u]);
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
int main() {
|
|
|
|
|
cin >> n;
|
|
|
|
|
memset(h, -1, sizeof h); // 初始化邻接表
|
|
|
|
|
for (int i = 1; i < n; i++) { // n-1条边
|
|
|
|
|
int a, b, c;
|
|
|
|
|
cin >> a >> b >> c;
|
|
|
|
|
add(a, b, c), add(b, a, c); // 换根dp一般用于无向图
|
|
|
|
|
}
|
|
|
|
|
dfs(1); // 任选一个点作为根节点,此处选择的是肯定存在的1号结点
|
|
|
|
|
cout << ans << endl;
|
|
|
|
|
return 0;
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
## 换根$DP$
|
|
|
|
|
|
|
|
|
|
@ -344,85 +398,333 @@ int main() {
|
|
|
|
|
|
|
|
|
|
**三、$O(N)$算法**
|
|
|
|
|
如果$n=1e6$,那么就要考虑换根$dp$了
|
|
|
|
|
我们考虑相邻的医院是否存在转换关系
|
|
|
|
|
设其中一个医院为u(父节点),另一个为v(子节点)
|
|
|
|
|
如果把u点的医院改为v点,则发现:
|
|
|
|
|
以v为根的子树的集合的所有人少走1步,但是另一集合的所有人要多走一步
|
|
|
|
|
设siz[i]表示以i为根节点的集合人的总数,dp[i]表示在i点设置医院的代价,则可转换成:
|
|
|
|
|
dp[v]=dp[u]+(siz[1]-siz[v])-siz[v]:其中siz[1]表示全部人的数量
|
|
|
|
|
思路:
|
|
|
|
|
1.先算出1个点的代价,之后dp换根直接转换
|
|
|
|
|
我们考虑相邻的医院是否存在转换关系,设其中一个医院为$u$(父节点),另一个为$v$(子节点)
|
|
|
|
|
如果把$u$点的医院改为$v$点,则发现:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如图:以$5$为根时:
|
|
|
|
|
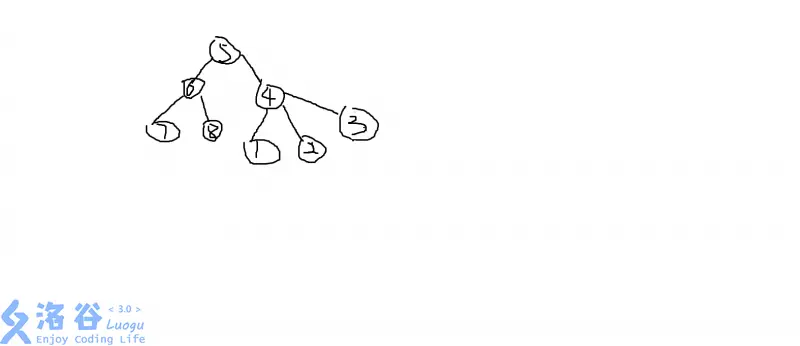
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以$4$为根时:
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以$v$为根的子树的集合的所有人少走$1$步,但是另一集合的所有人要多走一步
|
|
|
|
|
|
|
|
|
|
#### [$P2986$ $Great$ $Cow$ $Gathering$ $G$](https://www.luogu.com.cn/problem/P2986)
|
|
|
|
|
https://blog.csdn.net/zstuyyyyccccbbbb/article/details/108952302
|
|
|
|
|
设$sz[i]$表示以$i$为根节点的集合人的总数,$f[i]$表示在$i$点设置医院的代价,则可转换成:
|
|
|
|
|
$$\large f[v]=f[u]+(sz[1]-sz[v])-sz[v]=f[u]+sz[1]-2\times sz[v]$$
|
|
|
|
|
> **注**: 其中$sz[1]$表示全部人的数量,一般也写做$n$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CF1324F.Maximum White Subtree
|
|
|
|
|
**思路**:
|
|
|
|
|
先算出$1$个点的代价,之后$dp$换根直接转换
|
|
|
|
|
|
|
|
|
|
[USACO12FEB]Nearby Cows G
|
|
|
|
|
**$Code$**
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
using namespace std;
|
|
|
|
|
const int N = 1e5 + 10, M = N << 1;
|
|
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
|
|
|
|
|
|
|
// 链式前向星
|
|
|
|
|
int e[M], h[N], idx, w[M], ne[M];
|
|
|
|
|
void add(int a, int b, int c = 0) {
|
|
|
|
|
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
|
|
|
|
|
}
|
|
|
|
|
int c[N];
|
|
|
|
|
int f[N], sz[N];
|
|
|
|
|
int ans = INF;
|
|
|
|
|
|
|
|
|
|
// 第一次dfs,获取在以1为根的树中:
|
|
|
|
|
// 1、每个节点分别有多少个子节点,填充sz[]数组
|
|
|
|
|
// 2、获取到f[1],f[1]表示在1点设置医院的代价
|
|
|
|
|
// 获取到上面这一组+一个数据,才能进行dfs2进行换根
|
|
|
|
|
void dfs1(int u, int fa, int step) {
|
|
|
|
|
sz[u] = c[u]; // 这个挺绝啊~,与一般的统计子树节点个数不同,这里把人数,也就是点权值,也看做是一个节子点,想想也是这个道理
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
int v = e[i];
|
|
|
|
|
if (v == fa) continue;
|
|
|
|
|
dfs1(v, u, step + 1); // 填充深搜v节点为根的子树
|
|
|
|
|
sz[u] += sz[v]; // 在完成了v节点的数据统计后,用v节点的sz[v]结果累加到sz[u]
|
|
|
|
|
}
|
|
|
|
|
f[1] += step * c[u]; // 累加步数*人数 = 1点的总代价,预处理出1点的总代价
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
// 第二次dfs,开始dp换根
|
|
|
|
|
void dfs2(int u, int fa) {
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
int v = e[i];
|
|
|
|
|
if (v == fa) continue;
|
|
|
|
|
f[v] = f[u] + sz[1] - sz[v] * 2; // 经典的递推式
|
|
|
|
|
dfs2(v, u); // 继续深搜
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
int main() {
|
|
|
|
|
// 初始化链式前向星
|
|
|
|
|
memset(h, -1, sizeof h);
|
|
|
|
|
|
|
|
|
|
int n;
|
|
|
|
|
cin >> n;
|
|
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
|
|
cin >> c[i];
|
|
|
|
|
int a, b;
|
|
|
|
|
cin >> a >> b;
|
|
|
|
|
if (a) add(a, i), add(i, a); // 是一个二叉树结构,与左右节点相链接,但有可能不存在左或右节点,不存在时,a或b为0
|
|
|
|
|
if (b) add(b, i), add(i, b);
|
|
|
|
|
}
|
|
|
|
|
// 1、准备动作
|
|
|
|
|
dfs1(1, 0, 0);
|
|
|
|
|
// 2、换根dp
|
|
|
|
|
dfs2(1, 0);
|
|
|
|
|
|
|
|
|
|
[COCI2014-2015#1]Kamp
|
|
|
|
|
// 输出答案
|
|
|
|
|
for (int i = 1; i <= n; i++) ans = min(ans, f[i]);
|
|
|
|
|
cout << ans << endl;
|
|
|
|
|
return 0;
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
[APIO2014]连珠线
|
|
|
|
|
#### [$P2986$ 伟大的奶牛聚集](https://www.luogu.com.cn/problem/P2986)
|
|
|
|
|
|
|
|
|
|
POJ3585 Accumulation Degree
|
|
|
|
|
**题目描述**
|
|
|
|
|
|
|
|
|
|
CF708C Centroids
|
|
|
|
|
$Bessie$ 正在计划一年一度的奶牛大集会,来自全国各地的奶牛将来参加这一次集会。当然,她会选择最方便的地点来举办这次集会。
|
|
|
|
|
|
|
|
|
|
每个奶牛居住在 $N$ 个农场中的一个,这些农场由 $N-1$ 条道路连接,并且从任意一个农场都能够到达另外一个农场。道路 $i$ 连接农场 $A_i$ 和 $B_i$,长度为 $L_i$。集会可以在 $N$ 个农场中的任意一个举行。另外,每个牛棚中居住着 $C_i$ 只奶牛。
|
|
|
|
|
|
|
|
|
|
#### [$AcWing$ $1072$ 树的最长路径](https://www.cnblogs.com/littlehb/p/15784687.html)
|
|
|
|
|
在选择集会的地点的时候,Bessie 希望最大化方便的程度(也就是最小化不方便程度)。比如选择第 $X$ 个农场作为集会地点,它的不方便程度是其它牛棚中每只奶牛去参加集会所走的路程之和(比如,农场 $i$ 到达农场 $X$ 的距离是 $20$,那么总路程就是 $C_i\times 20$)。帮助 $Bessie$ 找出最方便的地点来举行大集会。
|
|
|
|
|
|
|
|
|
|
**题目分析**
|
|
|
|
|
这还分析个啥啊,这不就是上一道题的医院选址吗?
|
|
|
|
|
|
|
|
|
|
**$Code$**
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
|
|
|
|
using namespace std;
|
|
|
|
|
const int N = 10010, M = N << 1;
|
|
|
|
|
int n; // n个结点
|
|
|
|
|
const int N = 1e5 + 10, M = N << 1;
|
|
|
|
|
#define int long long
|
|
|
|
|
#define endl "\n"
|
|
|
|
|
|
|
|
|
|
// 链式前向星
|
|
|
|
|
int h[N], e[M], w[M], ne[M], idx;
|
|
|
|
|
void add(int a, int b, int c) {
|
|
|
|
|
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
|
|
|
|
|
int e[M], h[N], idx, w[M], ne[M];
|
|
|
|
|
void add(int a, int b, int c = 0) {
|
|
|
|
|
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
// 换根dp模板
|
|
|
|
|
int ans; // 答案,直径
|
|
|
|
|
int d1[N], d2[N]; // d1[i],d2[i]:经过i点的最长,次长长度是多少
|
|
|
|
|
bool st[N]; // 是不是遍历过了
|
|
|
|
|
void dfs(int u) {
|
|
|
|
|
st[u] = true;
|
|
|
|
|
int c[N]; // 点权数组
|
|
|
|
|
int sz[N]; // sz[i]:在以1号节点为根时,i号节点的子节点数量
|
|
|
|
|
int dis[N]; // dis[i]:表示i距离起点的长度
|
|
|
|
|
int f[N]; // f[i]:把奶牛大集会的地点设为i时的最小代价
|
|
|
|
|
int ans = 1e18;
|
|
|
|
|
|
|
|
|
|
// 第一次dfs,获取在以1为根的树中:
|
|
|
|
|
// 1、每个节点分别有多少个子节点,填充sz[]数组
|
|
|
|
|
// 2、获取到f[1],f[1]表示在1点设置医院的代价
|
|
|
|
|
// 获取到上面这一组+一个数据,才能进行dfs2进行换根
|
|
|
|
|
void dfs1(int u, int fa) {
|
|
|
|
|
sz[u] = c[u]; // 这个和医院选址是一样的,点权就是子节点个数
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
int v = e[i];
|
|
|
|
|
if (st[v]) continue; // v点访问过了
|
|
|
|
|
|
|
|
|
|
// 走v子树,完成后,v子树中每个节点的d1[v],d2[v]都已经准备好,u节点可以直接利用
|
|
|
|
|
dfs(v);
|
|
|
|
|
if (v == fa) continue;
|
|
|
|
|
dis[v] = dis[u] + w[i]; // 每个点到根节点的距离,这个和医院选址是不一样的,那个是一步+1,用step记录即可,这个还有边权
|
|
|
|
|
dfs1(v, u); // 深搜
|
|
|
|
|
sz[u] += sz[v]; // 以u为根的子树奶牛数量
|
|
|
|
|
}
|
|
|
|
|
f[1] += dis[u] * c[u]; // 累加 距离*人数=1点的总代价
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
// w[i]:u->v的路径长度,d1[u]:最长路径,d2[u]:次长路径
|
|
|
|
|
if (d1[v] + w[i] >= d1[u]) // v可以用来更新u的最大值
|
|
|
|
|
d2[u] = d1[u], d1[u] = d1[v] + w[i]; // 最长路转移
|
|
|
|
|
else if (d1[v] + w[i] > d2[u])
|
|
|
|
|
d2[u] = d1[v] + w[i]; // 次长路转移
|
|
|
|
|
// 第二次dfs,开始dp换根
|
|
|
|
|
void dfs2(int u, int fa) {
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
int v = e[i];
|
|
|
|
|
if (v == fa) continue;
|
|
|
|
|
f[v] = f[u] + (sz[1] - sz[v] * 2) * w[i];
|
|
|
|
|
dfs2(v, u);
|
|
|
|
|
}
|
|
|
|
|
// 更新结果
|
|
|
|
|
ans = max(ans, d1[u] + d2[u]);
|
|
|
|
|
}
|
|
|
|
|
signed main() {
|
|
|
|
|
// 初始化链式前向星
|
|
|
|
|
memset(h, -1, sizeof h);
|
|
|
|
|
|
|
|
|
|
int main() {
|
|
|
|
|
int n;
|
|
|
|
|
cin >> n;
|
|
|
|
|
memset(h, -1, sizeof h); // 初始化邻接表
|
|
|
|
|
for (int i = 1; i < n; i++) { // n-1条边
|
|
|
|
|
for (int i = 1; i <= n; i++) cin >> c[i];
|
|
|
|
|
for (int i = 1; i < n; i++) {
|
|
|
|
|
int a, b, c;
|
|
|
|
|
cin >> a >> b >> c;
|
|
|
|
|
add(a, b, c), add(b, a, c); // 换根dp一般用于无向图
|
|
|
|
|
add(a, b, c), add(b, a, c);
|
|
|
|
|
}
|
|
|
|
|
dfs(1); // 任选一个点作为根节点,此处选择的是肯定存在的1号结点
|
|
|
|
|
// 1、准备动作
|
|
|
|
|
dfs1(1, 0);
|
|
|
|
|
// 2、换根dp
|
|
|
|
|
dfs2(1, 0);
|
|
|
|
|
// 输出答案
|
|
|
|
|
for (int i = 1; i <= n; i++) ans = min(ans, f[i]);
|
|
|
|
|
cout << ans << endl;
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
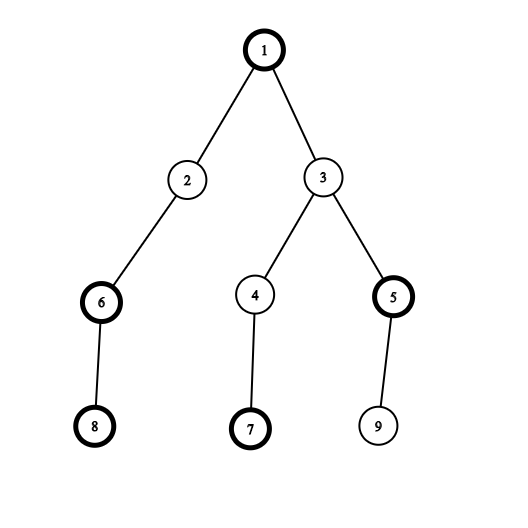
#### [$CF1324F$.$Maximum$ $White$ $Subtree$](https://codeforces.com/problemset/problem/1324/F)
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
**思路分析**
|
|
|
|
|
这题要求的是求出对任何一个节点$v$,求出包含这个节点的子树$cnt_1−cnt_2$的最大值。
|
|
|
|
|
|
|
|
|
|
#### 暴力想法
|
|
|
|
|
首先思考下暴力写法应该如何写。
|
|
|
|
|
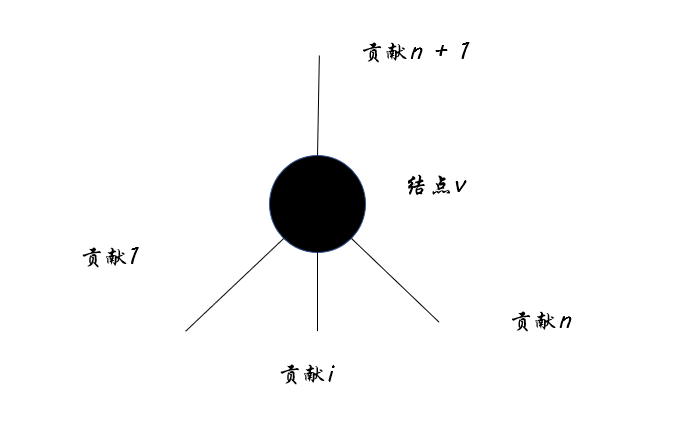
|
|
|
|
|
|
|
|
|
|
对于所有可能的路径的贡献值的累加,且贡献值需大于等于$0$。
|
|
|
|
|
>- 白的比黑的多,有分, 这时我们选上这棵子树
|
|
|
|
|
>- 黑的比白的多,没分, 这时我们放弃这棵子树
|
|
|
|
|
|
|
|
|
|
不妨设$f[u]$代表$u$结点的最大值。故
|
|
|
|
|
|
|
|
|
|
$$\large f[u]=c[u]+\sum_{v \in son_u}max(0,f[v])$$
|
|
|
|
|
|
|
|
|
|
假如用暴力写法,就是对于每个结点$u$,暴力搜索所有的相邻结点,利用$dfs$暴力搜索。也就是以每个结点为棵出发,枚举$n$次$dfs$,但是结点最大为$2∗10^5$ 这个暴力算法显然会超时,考虑如何优化。
|
|
|
|
|
|
|
|
|
|
#### 算法优化
|
|
|
|
|
对于从下往上的贡献,可以利用从下往上的$dfs$树形$dp$进行获取,难求的是刨去以$v$为根的子树的贡献值,也就是向上走的那部分。
|
|
|
|
|
|
|
|
|
|
设$u$为节点$v$的父节点,$f[v]$代表从下往上以$v$为根的 **白点数减去黑点数** 的 **最大值**,$g[v]$代表最终的最大值。
|
|
|
|
|
|
|
|
|
|
根据刨去以$v$为根的子树的贡献值这个思想,可以发现:
|
|
|
|
|
|
|
|
|
|
$$\large add=g[u]−max(0,f[v])$$
|
|
|
|
|
> **注**:$fa[v]=u$
|
|
|
|
|
|
|
|
|
|
就是刨去以$v$为根的子树的贡献值。写出状态转移方程:
|
|
|
|
|
$$\large g[v] =
|
|
|
|
|
\left\{\begin{matrix}
|
|
|
|
|
f[v] & if \ v = root \\
|
|
|
|
|
f[v]+max(0,g[u]-max(0,f[v]))& if \ v \neq root
|
|
|
|
|
\end{matrix}\right.
|
|
|
|
|
$$
|
|
|
|
|
|
|
|
|
|
因此思路:
|
|
|
|
|
|
|
|
|
|
- ① 从下往上树形$dp$,计算$f[v]$
|
|
|
|
|
- ② 从上往下换根$dp$,计算$g[v]$
|
|
|
|
|
|
|
|
|
|
**$Code$**
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
using namespace std;
|
|
|
|
|
const int N = 2e5 + 10, M = N << 1;
|
|
|
|
|
|
|
|
|
|
// 链式前向星
|
|
|
|
|
int e[M], h[N], idx, w[M], ne[M];
|
|
|
|
|
void add(int a, int b, int c = 0) {
|
|
|
|
|
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
int f[N];
|
|
|
|
|
int g[N];
|
|
|
|
|
int c[N]; // 颜色
|
|
|
|
|
int n; // 节点数量
|
|
|
|
|
|
|
|
|
|
// 以1号节点为根,跑一遍dfs,填充每个节点的cnt1-cnt2的最大值
|
|
|
|
|
void dfs1(int u, int fa) {
|
|
|
|
|
f[u] = c[u]; // 1:白色,-1黑色,正好与 cnt1-cnt2一致,初始值加上了老头子自己的养老钱
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
int v = e[i];
|
|
|
|
|
if (v == fa) continue;
|
|
|
|
|
dfs1(v, u);
|
|
|
|
|
f[u] += max(0, f[v]); // 如果我儿子给我,那我就拿着;如果我儿子不给我钱,或者管我要钱,我就不理它!
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
// 换根dp
|
|
|
|
|
void dfs2(int u, int fa) {
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
int v = e[i];
|
|
|
|
|
if (v == fa) continue;
|
|
|
|
|
int val = g[u] - max(f[v], 0);
|
|
|
|
|
g[v] = f[v] + max(val, 0);
|
|
|
|
|
dfs2(v, u);
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
int main() {
|
|
|
|
|
// 初始化链式前向星
|
|
|
|
|
memset(h, -1, sizeof h);
|
|
|
|
|
cin >> n;
|
|
|
|
|
|
|
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
|
|
int x;
|
|
|
|
|
cin >> x;
|
|
|
|
|
c[i] = (x ? x : -1); // 白色c[i]=1,黑色c[i]=-1
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
for (int i = 1; i < n; i++) {
|
|
|
|
|
int a, b;
|
|
|
|
|
cin >> a >> b;
|
|
|
|
|
add(a, b), add(b, a);
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
// 第一次dfs
|
|
|
|
|
dfs1(1, 0);
|
|
|
|
|
|
|
|
|
|
// 它们两个是一个意思
|
|
|
|
|
g[1] = f[1];
|
|
|
|
|
// 换根dp
|
|
|
|
|
dfs2(1, 0);
|
|
|
|
|
// 输出答案
|
|
|
|
|
for (int i = 1; i <= n; i++) printf("%d ", g[i]);
|
|
|
|
|
return 0;
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
#### [$P3047$ $Nearby$ $Cows$ $G$](https://www.luogu.com.cn/problem/P3047)
|
|
|
|
|
|
|
|
|
|
**题目大意**
|
|
|
|
|
题目大意是给你一颗树,对于每一个节点$i$,求出范围$k$之内的点权之和。
|
|
|
|
|
|
|
|
|
|
看数据范围就知道暴力肯定是会$TLE$飞的,所以我们要考虑如何$dp$(代码习惯写$dfs$)
|
|
|
|
|
|
|
|
|
|
仔细思考一下我们发现点$i$走$k$步能到达的点分为以下两种
|
|
|
|
|
|
|
|
|
|
- 在$i$的子树中(由$i$点往下)
|
|
|
|
|
- 经过$i$的父亲(由$i$点往上)
|
|
|
|
|
|
|
|
|
|
这样的问题一般可以用两次$dfs$解决
|
|
|
|
|
|
|
|
|
|
定义状态:
|
|
|
|
|
- $f[i][j]$表示$i$点往下$j$步范围内的点权之和
|
|
|
|
|
- $g[i][j]$表示$i$点往上和往下走$j$步范围内点权之和
|
|
|
|
|
|
|
|
|
|
第一次$dfs$我们求出所有的$f[n][k]$,这个比较简单,对于节点$u$和其儿子$v$,$f[u][k] += f[v][j - 1]$就行了。(第一次$dfs$已知叶子节点推父亲节点)
|
|
|
|
|
|
|
|
|
|
第二次$dfs$我们通过已经求出的$f$数组推$g$数组,对于$u$和$u$的儿子$v$,
|
|
|
|
|
$$g[v][k] += (g[u][k - 1] - f[v][k - 2])$$
|
|
|
|
|
|
|
|
|
|
注意数组下表不要越界。$g[i][j]$的初始值应该赋为$f[i][j]$,因为根节点的$g[i][j]$就是$f[i][j]$。(第二次$dfs$已知父亲节点推儿子节点)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### [$P6419$ $Kamp$](https://www.luogu.com.cn/problem/P6419)
|
|
|
|
|
https://www.cnblogs.com/Troverld/p/14601347.html
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### [$P3647$ $APIO2014$ 连珠线](https://www.luogu.com.cn/problem/P3647)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### [$POJ3585$ $Accumulation$ $Degree$](http://poj.org/problem?id=3585)
|
|
|
|
|
https://blog.csdn.net/qq_34493840/article/details/90575293
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### [$CF708C$ $Centroids$](https://www.luogu.com.cn/problem/CF708C)
|
|
|
|
|
https://www.cnblogs.com/DongPD/p/17498336.html
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### [Eg3: AT Educational DP Contest V-Subtree](https://dmoj.ca/problem/dpv)
|
|
|
|
|
|
|
|
|
|
#### [$AcWing$ $1073$. 树的中心](https://www.cnblogs.com/littlehb/p/15786805.html)
|
|
|
|
|
|
|
|
|
|
#### [$AcWing$ $1148$ 秘密的牛奶运输](https://www.cnblogs.com/littlehb/p/16054005.html)
|