|
|
|
|
@ -42,12 +42,13 @@ $1≤T≤10,1≤n≤1000,1≤a_i≤10^9$
|
|
|
|
|
|
|
|
|
|
即:$(left[i][j],\underbrace{a_i,a_{i+1},\cdots,a_j}_{a[i]\sim a[j]})$,$(\underbrace{a_i,a_{i+1},\cdots,a_j}_{a[i]\sim a[j]},right[i][j])$ 为 **先手必败** 局面
|
|
|
|
|
|
|
|
|
|
有如下两个性质:
|
|
|
|
|
|
|
|
|
|
#### 2、性质1 $left[i][j]$,$right[i][j]$一定存在
|
|
|
|
|
#### 2、$left[i][j]$,$right[i][j]$一定存在
|
|
|
|
|
**反证法**:
|
|
|
|
|
假设不存在满足定义的 $left[i][j]$,则对于 **任意正整数** $x$,有形如:
|
|
|
|
|
假设不存在满足定义的 $left[i][j]$,则对于 **任意非负整数** $x$,有形如:
|
|
|
|
|
|
|
|
|
|
$$\large \underbrace{x,a_i,a_{i+1},\cdots,a_j}_{A(x)}$$ 都为**必胜局面**,记为 $A(x)$ 局面。
|
|
|
|
|
$$\large \underbrace{x,a_i,a_{i+1},\cdots,a_j}_{A(x)}$$ 都为 **必胜局面** ,记为 $A(x)$ 局面。
|
|
|
|
|
|
|
|
|
|
由于 $A(x)$ 为必胜局面,故从 $A(x)$ 局面 <font color='red' size=4><b>必然存在若干种办法一步可达必败局面</b></font>。
|
|
|
|
|
|
|
|
|
|
@ -55,27 +56,23 @@ $$\large \underbrace{x,a_i,a_{i+1},\cdots,a_j}_{A(x)}$$ 都为**必胜局面**,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
左边拿没用,只能考虑从右边拿(即从$a_j$里拿):
|
|
|
|
|
于是设 $A(x)$ 一步可达的(某个)**必败局面**为 $(x,a_i,a_{i+1},\cdots,a_{j-1},y)$,显然有 $0 \le y < a_j$。
|
|
|
|
|
|
|
|
|
|
**由于 $x$ 有无限个,但 $y$ 只有 $a_j$种——根据抽屉原理,必存在 $x_1,x_2(x_1 > x_2),y$ 满足 $(x_1,a_i,a_{i+1},\cdots,a_{j-1},y)$ 和 $(x_2,a_i,a_{i+1},\cdots,a_{j-1},y)$ 都是必败局面**。但这两个必败局面之间 **实际一步可达**(比如拿走$x_1-x_2$个),矛盾,假设不成,原命题成立。
|
|
|
|
|
于是设 $A(x)$ 一步可达的某个 **必败局面**为 $(x,a_i,a_{i+1},\cdots,a_{j-1},y)$,显然有 $0 \le y < a_j$。
|
|
|
|
|
|
|
|
|
|
#### 3、性质2 $left[i][j]$,$right[i][j]$必然唯一
|
|
|
|
|
**由于 $x$ 有无限个,但 $y$ 只有 $a_j$种——根据抽屉原理,必然存在 $x_1,x_2(x_1 > x_2),y$ 满足 $(x_1,a_i,a_{i+1},\cdots,a_{j-1},y)$ 和 $(x_2,a_i,a_{i+1},\cdots,a_{j-1},y)$ 都是必败局面**。但这两个必败局面之间 **实际一步可达**(比如拿走$x_1-x_2$个),矛盾,假设不成立,原命题成立。
|
|
|
|
|
|
|
|
|
|
#### 3、$left[i][j]$,$right[i][j]$必然唯一
|
|
|
|
|
|
|
|
|
|
**反证法**:
|
|
|
|
|
假设 $left(i,j)$ 不唯一,则存在非负整数 $x_1,x_2(x_1 \neq x_2)$,使得$(x_1,a_i,a_{i+1},⋯,a_{j−1},a_j)$ 和 $(x_2,a_i,a_{i+1},\cdots,a_{j-1},a_j)$ 均为必败局面,而 **第一个必败局面** 可以通过拿走左侧$x_1-x_2$个石子到达另一个 **必败局面** ,矛盾,假设不成立,原命题成立。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
### 五、状态转移
|
|
|
|
|
|
|
|
|
|
#### 1、边界情况
|
|
|
|
|
#### 4、边界情况
|
|
|
|
|
$$\LARGE left[i][i]=a_i$$
|
|
|
|
|
|
|
|
|
|
当只有一堆石子时,我在这堆前面添加一堆,个数和这堆一样多,对于**两堆相同的石子**,**后手进行和先手对称的操作**,你咋干我就咋干,我拿完,你瞪眼~, **先手必败**
|
|
|
|
|
|
|
|
|
|
#### 2、递推关系
|
|
|
|
|
#### 5、递推关系
|
|
|
|
|
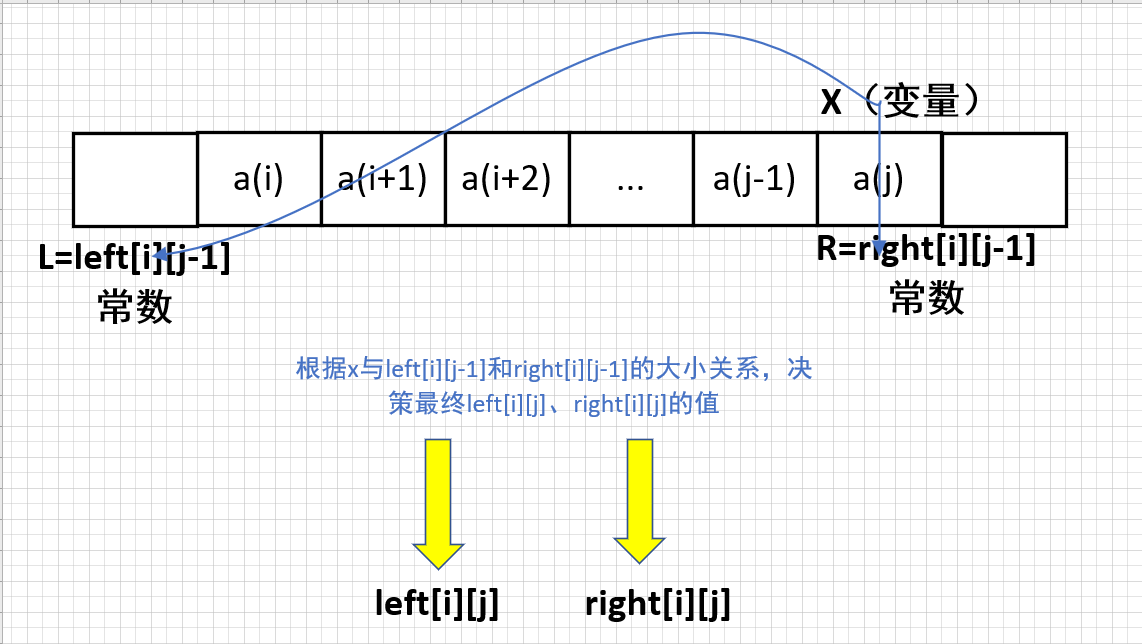
* 变化方法:从左侧拿走一些石子或者从右侧拿走一些石子
|
|
|
|
|
* 让我们使用$left[i][j-1]$和$right[i][j-1]$来表示$left[i][j]$和$right[i][j]$,形成$DP$递推关系
|
|
|
|
|
|
|
|
|
|
@ -83,11 +80,11 @@ $$\LARGE left[i][i]=a_i$$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 3、推论
|
|
|
|
|
#### 6、推论
|
|
|
|
|
有了上面推的$left[i][j]$唯一性,得出一个有用的推论:
|
|
|
|
|
**对于任意非负整数 $x \neq left(i,j)$,$\large (x,a_i,a_{i+1},\cdots,a_j)$为必胜局面**
|
|
|
|
|
|
|
|
|
|
#### 4、特殊情况:$L=R=0$
|
|
|
|
|
#### 7、特殊情况:$L=R=0$
|
|
|
|
|
为方便叙述,下文记 $left[i][j-1]$ 为 $L$,记 $right[i][j-1]$ 为 $R$,并令 $\displaystyle \large x=a_j(x>0)$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
@ -96,7 +93,7 @@ $$\LARGE left[i][i]=a_i$$
|
|
|
|
|
<font color='red'><b>注:因$R=0$,表示在[$i$,$j-1$]确定后,右侧为$0$就能满足[$i$,$j-1$]这一段为先手必败,此时,左侧增加那堆个数为$0$就可以继续保持原来的先手必败,即$L=0$。</b></font>
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 5、分类讨论
|
|
|
|
|
#### 8、分类讨论
|
|
|
|
|
|
|
|
|
|
* $x=R$($Case$ $1$)
|
|
|
|
|
最简单的情况——根据 $R=right[i][j-1]$ 的定义,区间 $[i,j]$ 本来就是必败局面,因此左边啥也不能添,添了反而错,故
|
|
|
|
|
|