'commit'

TangDou/ChatGPT/学习笔记.md

@@ -0,0 +1,7 @@
+【昨晚课程回放和课件】：https://www.zhihu.com/xen/training/live/room/1734236558582992898/1734236796119171072
+
+第一天到课福利四大$ai$工具：
+Gamma：https://gamma.app/
+ChatDoc：https://chatdoc.com/
+ChatExcel：https://chatexcel.com/
+ChatMind：https://www.chatmind.tech/

TangDou/Geogebra/听课笔记.md

@@ -18,4 +18,17 @@
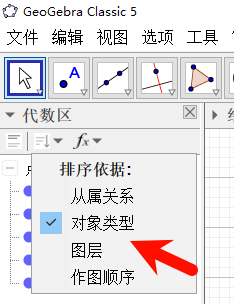
 #### 1.1 用工具和属性绘制简单图形
 ![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401311531627.png)
 
-**[$GeoGebra$如何擦除踪迹——移动视图、放大、设置活动视图](https://zhuanlan.zhihu.com/p/298051355)**
+**[$GeoGebra$如何擦除踪迹——移动视图、放大、设置活动视图](https://zhuanlan.zhihu.com/p/298051355)**
+
+
+#### 实验：抛物线方程$y=ax^2+bx+c$,如果只变化$b$, 那么顶点的坐标轨迹为什么是一条抛物线呢？
+
+答：抛物线方程为 $y=ax^2+bx+c$ 
+ 
+当 $b$ 变化时，顶点的横坐标为 $x=-\frac{b}{2a}$ 
+ 
+将 $x$ 代入原方程，得到顶点的纵坐标为 $y=\frac{b^2}{4a}-c$ 
+ 
+因此，顶点的坐标轨迹为 $y=\frac{b^2}{4a}-c$ 
+ 
+这是一个关于 $b$ 的二次函数，其图像为一条抛物线。