From d4db8dbc76f45295e445e72dca758d47370b56a6 Mon Sep 17 00:00:00 2001
From: =?UTF-8?q?=E9=BB=84=E6=B5=B7?= <10402852@qq.com>
Date: Wed, 17 Jan 2024 10:18:38 +0800
Subject: [PATCH] 'commit'
---
TangDou/AcWing/Tree/1073.md | 44 ++--------------
TangDou/Topic/【换根DP】专题.md | 74 ++++++++++++++++++++++++++-
2 files changed, 78 insertions(+), 40 deletions(-)
diff --git a/TangDou/AcWing/Tree/1073.md b/TangDou/AcWing/Tree/1073.md
index 44e0f07..a39af66 100644
--- a/TangDou/AcWing/Tree/1073.md
+++ b/TangDou/AcWing/Tree/1073.md
@@ -118,10 +118,10 @@ int main() {
两者比较，取一个 $max$ 即可
-我们用 $d1[u],d2[u],up[u],p1[u]$分别存一下需要的信息，这些数据存的是：
-$d1[u]$：存下$u$节点向下走的最长路径的长度
-$d2[u]$：存下$u$节点向下走的第二长的路径的长度
-$p1[u]$：存下$u$节点向下走的最长路径是从哪一个节点下去的
+我们用 $mx1[u],mx2[u],up[u],id[u]$分别存一下需要的信息，这些数据存的是：
+$mx1[u]$：存下$u$节点向下走的最长路径的长度
+$mx2[u]$：存下$u$节点向下走的第二长的路径的长度
+$id[u]$：存下$u$节点向下走的最长路径是从哪一个节点下去的
$up[u]$：存下$u$节点向上走的最长路径的长度
#### 图解
@@ -202,38 +202,4 @@ int main() {
return 0;
}
-```
-
-**$Q1$:为什么$dfs1$中要 先安排工作，后统计信息？**
-$A$:因为后面$u$统计的信息，是根据多个子节点$j$的信息汇集统计来的，儿子的信息没出来，爹的信息就统计不出来，儿子需要先计算。
-
-**$Q2$:为什么$dfs2$中要 先统计信息，后安排工作？**
-$A$:这取决于继续递归前，是否需要前序提供信息，比如此处在处理子节点$j$时，需要更新$up[j]$,但$up[j]$是依赖于$up[u],d1[u],d2[u]$的，$d1[u],d2[u]$在$dfs1$中已完成填充，没有问题，但$up[u]$如果还没正确填充内容，后续就无法完成计算了,所以必须在进入递归前完成统计信息计算，为后面的子递归提供数据信息。
-
-**$Q3$:为什么非得跑一遍$dfs1$,再跑一遍$dfs2$,只跑一遍不行吗？**
-$A$:第一遍$dfs$，解决的是我的孩子到我有多远的问题，没有记录，也没法记录 我爹，我爷爷离我有多远的问题，那需要再跑一遍反向的才能知道。
-
-
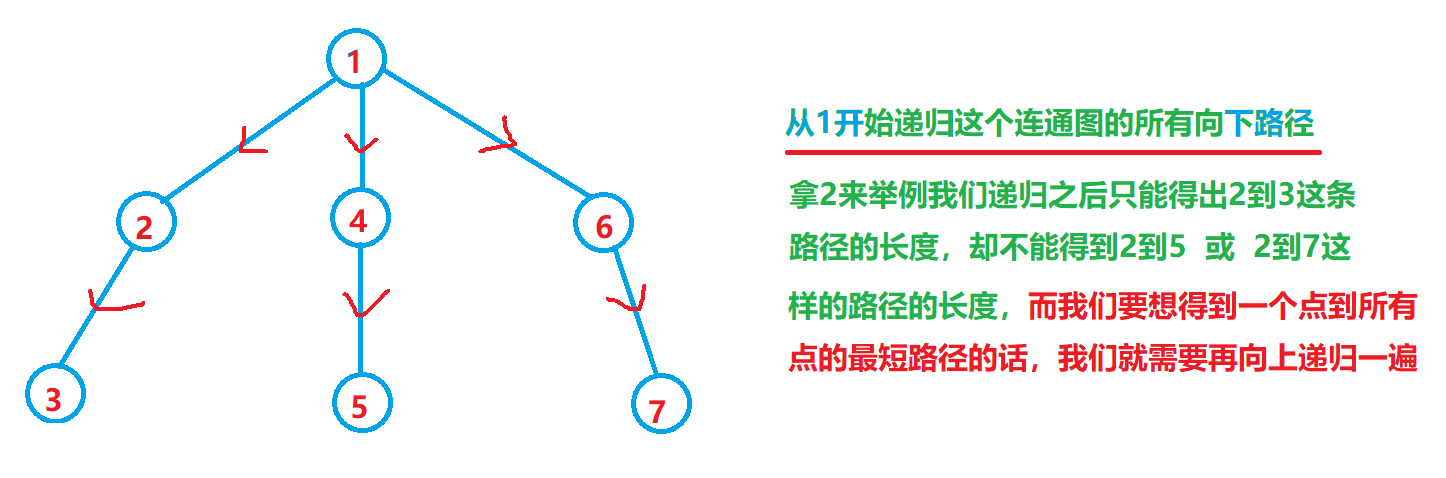-**$Q4$:据说边权要是负的，需要修改代码，该怎么改？**
-$A:$如下,把下面两句注释的话放开即可
-
-```cpp {.line-numbers}
-void dfs1(int u) {
- // d1[u] = d2[u] = -INF; //这题所有边权都是正的，可以不用初始化为负无穷
- st[u]=1;
- for (int i = h[u]; ~i; i = ne[i]) {
- int j = e[i];
- if (st[j]) continue;
-
- dfs1(j);
-
- if (d1[j] + w[i] >= d1[u]) {
- d2[u] = d1[u];
- d1[u] = d1[j] + w[i];
- p1[u] = j;
- } else if (d1[j] + w[i] > d2[u])
- d2[u] = d1[j] + w[i];
- }
- // if (d1[u] == -INF) d1[u] = d2[u] = 0; //特判叶子结点
-}
-```
+```
\ No newline at end of file
diff --git a/TangDou/Topic/【换根DP】专题.md b/TangDou/Topic/【换根DP】专题.md
index c9aac9a..de23f24 100644
--- a/TangDou/Topic/【换根DP】专题.md
+++ b/TangDou/Topic/【换根DP】专题.md
@@ -952,6 +952,79 @@ int main() {
return 0;
}
```
+#### [$AcWing$ $1073$. 树的中心](https://www.cnblogs.com/littlehb/p/15786805.html)
+
+[题解](https://www.cnblogs.com/littlehb/p/15786805.html)
+```cpp {.line-numbers}
+#include
+using namespace std;
+
+const int N = 10010, M = N << 1;
+const int INF = 0x3f3f3f3f;
+
+int n; // n个节点
+int mx1[N]; // mx1[u]：u节点向下走的最长路径的长度
+int mx2[N]; // mx2[u]：u节点向下走的次长路径的长度
+int id[N]; // id[u]：u节点向下走的最长路径是从哪一个节点下去的
+int up[N]; // up[u]：u节点向上走的最长路径的长度
+
+// 邻接表
+int e[M], h[N], idx, w[M], ne[M];
+void add(int a, int b, int c = 0) {
+ e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
+}
+
+// 功能:以u为根，向叶子进行递归，利用子节点返回的最长信息，更新自己的最长和次长,并记录最长是从哪个节点来的
+void dfs1(int u, int fa) {
+ for (int i = h[u]; ~i; i = ne[i]) {
+ int v = e[i];
+ if (v == fa) continue;
+
+ // 递归完才能有数据
+ dfs1(v, u);
+ int x = mx1[v] + w[i]; // u问到：儿子v可以带我走多远？
+ if (mx1[u] < x) { // 更新最长
+ mx2[u] = mx1[u]; // ① 更新次长
+ mx1[u] = x; // ② 更新最长
+ id[u] = v; // ③ 记录最长来源
+ } else if (mx2[u] < x) // 更新次长
+ mx2[u] = x;
+ }
+}
+
+// 功能：完成向上的信息填充
+void dfs2(int u, int fa) {
+ for (int i = h[u]; ~i; i = ne[i]) {
+ int v = e[i];
+ if (v == fa) continue;
+ // 二者取其一
+ if (id[u] == v)
+ up[v] = max(mx2[u], up[u]) + w[i];
+ else
+ up[v] = max(mx1[u], up[u]) + w[i];
+ // 递归
+ dfs2(v, u);
+ }
+}
+
+int main() {
+ memset(h, -1, sizeof h);
+ cin >> n;
+ for (int i = 1; i < n; i++) {
+ int a, b, c;
+ cin >> a >> b >> c;
+ add(a, b, c), add(b, a, c);
+ }
+ dfs1(1, 0); // 选择任意一个节点进行dfs,用儿子更新父亲的统计信息
+ dfs2(1, 0); // 向上
+
+ int res = INF;
+ for (int i = 1; i <= n; i++) res = min(res, max(mx1[i], up[i]));
+ printf("%d\n", res);
+
+ return 0;
+}
+```
#### [$P6419$ $Kamp$](https://www.luogu.com.cn/problem/P6419)
**题目大意**
@@ -1193,7 +1266,6 @@ signed main() {
for (int i = 1; i <= n; i++) cout << g[i] - max(up[i], mx1[i]) << endl;
}
```
-#### [$AcWing$ $1073$. 树的中心](https://www.cnblogs.com/littlehb/p/15786805.html)
#### [$AcWing$ $1148$ 秘密的牛奶运输](https://www.cnblogs.com/littlehb/p/16054005.html)