From c85bea0aaf3fb7c9b26dfec182e59ce790947854 Mon Sep 17 00:00:00 2001
From: =?UTF-8?q?=E9=BB=84=E6=B5=B7?= <10402852@qq.com>
Date: Wed, 13 Mar 2024 16:45:08 +0800
Subject: [PATCH] 'commit'
---
TangDou/AcWing/BeiBao/1013.md | 41 +++++++-------
TangDou/AcWing/BeiBao/9.md | 8 ++-
TangDou/AcWing/BeiBao/背包问题专题.md | 62 +++++++++++++++++++++
3 files changed, 86 insertions(+), 25 deletions(-)
diff --git a/TangDou/AcWing/BeiBao/1013.md b/TangDou/AcWing/BeiBao/1013.md
index b8fe2fb..b59f7cd 100644
--- a/TangDou/AcWing/BeiBao/1013.md
+++ b/TangDou/AcWing/BeiBao/1013.md
@@ -77,8 +77,26 @@ $3$个公司，$3$台机器,**机器都是一样的，一样的，记住，一
**答**:$1$号公司得到$1$台机器，$2$号公司得到$1$台机器，$3$号公司得到$1$台机器，就是$30+20+20=70$,此时国家利益最大。
+### 二、分组背包
+转换成 **分组背包问题** ，做 **等价变换**
+
+
+① 第$i$个公司就是第$i$个分组
+② 每个分组中可以一台也不要，可以要一台，可以要两台,...,可以要$S_i$台
+
+
+**分组背包** 的 **闫氏DP分析法**
+
+
+
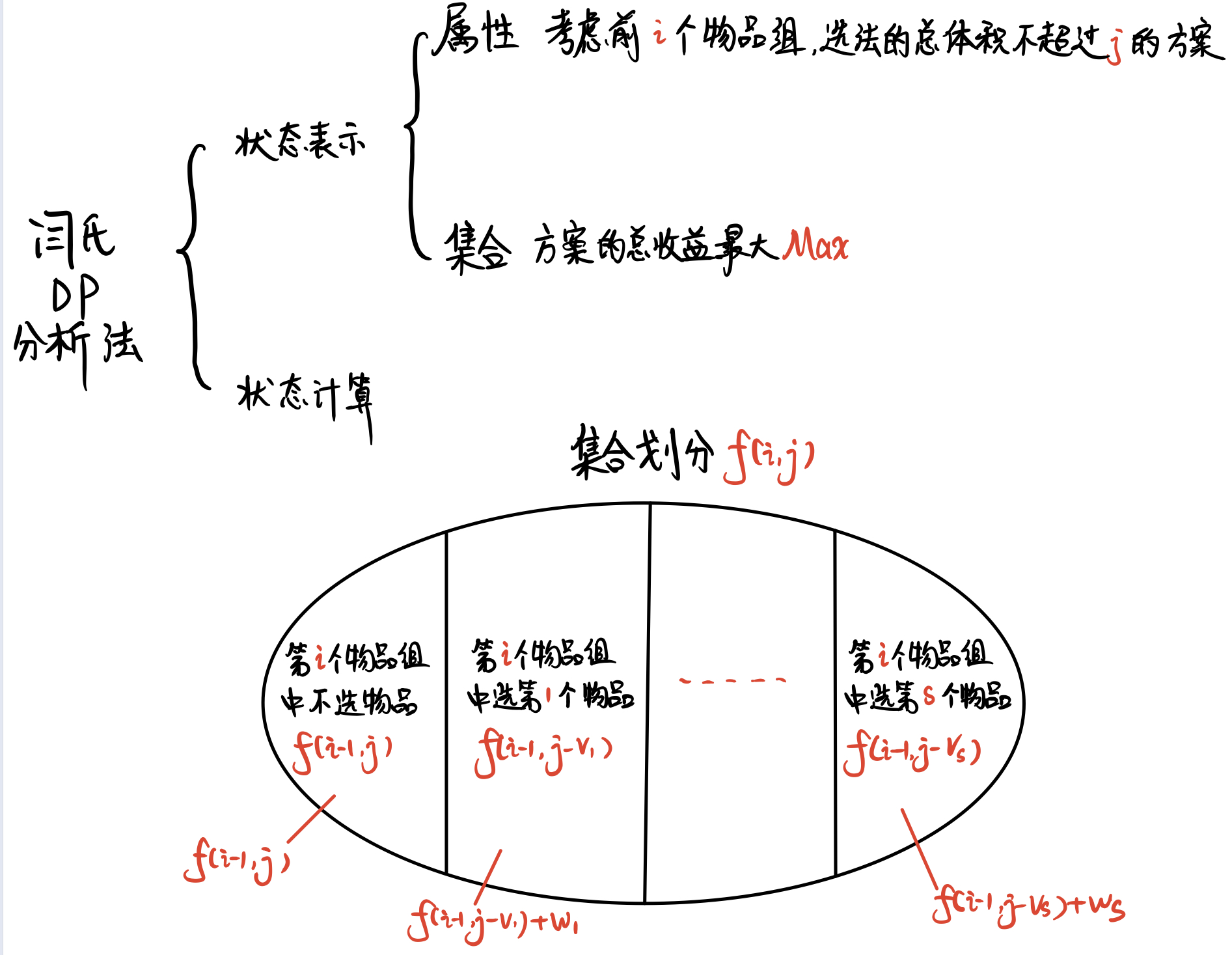+初始状态 ：$f[0][0]$
+
+目标状态 ：$f[N][M]$
+
+
### 三、不同$OJ$此题的差别
两者差别：
+
* $AcWing$：答案不唯一，输出任意合法方案即可($Special$ $Judge$)
* 洛谷: $P.S.$要求答案的字典序最小
@@ -123,27 +141,6 @@ for (int k = 1; k <= j; k++) {
$k$的含义是当前分组中的物品个数，是由小到大的。而这里的计算式是$j-k$,这个东西在$k$前面的符号是负数，也就是$k$越小，值越大，$k$越大，值越小。按个循环逻辑，随着$k$的长大，就会枚举到更小的$j-k$,也就是枚举到更小的字典序。如果没有等号，就是$k$越来越大时，$j-k$越来越小，当价值一样时，越来越小的个数无法更新结果，反之，如果有等号，就是获取到字典序。
-### 四、分组背包
-转换成 **背包$DP$** 问题，需要对里面的一些叙述做出 **等价变换**
-
-① 对于分给第$i$个公司的不同机器数量可以分别看作是一个物品组内的物品数量。
-
-② 物品$k$的含义：分给第$i$个公司$k$台机器
-
-③ 物品$k$的体积：因为一个机器算一个，所以体积也是$k$
-
-④ 物品$k$的价值：$w_{k}$
-
-
-
-直接上 **分组背包** 的 **闫氏DP分析法**
-
-
-
-初始状态 ：$f[0][0]$
-
-目标状态 ：$f[N][M]$
-
**二维数组写法**
```cpp {.line-numbers}
@@ -297,7 +294,7 @@ int main() {
```
### 四、深度优先搜索
-数据范围比较小，$1<=N<=10,1<=M<=15$,把$m$个机器分配给$n$个公司，暴力遍历所有方案
+数据范围比较小，$1 \leq N \leq 10,1 \leq M \leq 15$,把$m$个机器分配给$n$个公司，暴力遍历所有方案
记录分配方案，如果能更新最优解，顺便更新一下最优解的分配方案
diff --git a/TangDou/AcWing/BeiBao/9.md b/TangDou/AcWing/BeiBao/9.md
index 5c8f049..e4b994d 100644
--- a/TangDou/AcWing/BeiBao/9.md
+++ b/TangDou/AcWing/BeiBao/9.md
@@ -90,9 +90,10 @@ int main() {
cin >> v[i][j] >> w[i][j]; // 第i个分组中物品的体积和价值
}
- for (int i = 1; i <= n; i++)
- for (int j = 0; j <= m; j++) {
- for (int k = 0; k <= s[i]; k++)
+ for (int i = 1; i <= n; i++) // 每组
+ for (int j = 0; j <= m; j++) { // 每个合法体积
+ f[i][j] = f[i - 1][j]; // 如果一个都不要，那么这一组就相当于白费，给你机会也不中用，继承于i-1
+ for (int k = 1; k <= s[i]; k++) // 选择第k个
if (j >= v[i][k])
f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]); // 枚举每一个PK一下大小
}
@@ -100,6 +101,7 @@ int main() {
printf("%d", f[n][m]);
return 0;
}
+
```
### 四、一维数组版本
diff --git a/TangDou/AcWing/BeiBao/背包问题专题.md b/TangDou/AcWing/BeiBao/背包问题专题.md
index e19a6a2..9b32bbe 100644
--- a/TangDou/AcWing/BeiBao/背包问题专题.md
+++ b/TangDou/AcWing/BeiBao/背包问题专题.md
@@ -623,6 +623,68 @@ int main() {
### 八、分组背包
**[$AcWing$ $9$. 分组背包问题](https://www.acwing.com/problem/content/description/9/)**
+**二维状态**
+```cpp {.line-numbers}
+#include
+
+using namespace std;
+
+const int N = 110;
+int n, m;
+int f[N][N], v[N][N], w[N][N], s[N];
+
+int main() {
+ cin >> n >> m;
+ for (int i = 1; i <= n; i++) {
+ cin >> s[i]; // 第i个分组中物品个数
+ for (int j = 1; j <= s[i]; j++)
+ cin >> v[i][j] >> w[i][j]; // 第i个分组中物品的体积和价值
+ }
+
+ for (int i = 1; i <= n; i++) // 每组
+ for (int j = 0; j <= m; j++) { // 每个合法体积
+ f[i][j] = f[i - 1][j]; // 如果一个都不要，那么这一组就相当于白费，给你机会也不中用，继承于i-1
+ for (int k = 1; k <= s[i]; k++) // 选择第k个
+ if (j >= v[i][k])
+ f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]); // 枚举每一个PK一下大小
+ }
+ // 输出打表结果
+ printf("%d", f[n][m]);
+ return 0;
+}
+
+```
+
+**一维状态**
+```cpp {.line-numbers}
+#include
+
+using namespace std;
+const int N = 110;
+
+int n, m;
+int v[N][N], w[N][N], s[N];
+int f[N];
+
+int main() {
+ cin >> n >> m;
+
+ for (int i = 1; i <= n; i++) {
+ cin >> s[i];
+ for (int j = 1; j <= s[i]; j++)
+ cin >> v[i][j] >> w[i][j];
+ }
+
+ for (int i = 1; i <= n; i++)
+ for (int j = m; j >= 0; j--)
+ for (int k = 1; k <= s[i]; k++)
+ if (j >= v[i][k])
+ f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
+
+ printf("%d\n", f[m]);
+ return 0;
+}
+```
**[$AcWing$ $1013$. 机器分配](https://www.acwing.com/problem/content/1015/)**
分组背包求最优路径
\ No newline at end of file