'commit'

TangDou/AcWing/MinimalPath/1128.cpp

@@ -3,7 +3,7 @@ using namespace std;
 typedef pair<int, int> PII;
 const int INF = 0x3f3f3f3f;
 const int N = 110;
-const int M = 2 * 210; // 无向边，开两倍
+const int M = 2 * 210; // 无向图，需要开二倍的数组长度！
 
 int n, m;
 int h[N], e[M], w[M], ne[M], idx;
@@ -14,19 +14,18 @@ int dis[N];
 bool st[N];
 
 int dijkstra() {
-    // 初始化为正无穷
     memset(dis, 0x3f, sizeof dis);
-    dis[1] = 0; // 1号点为出发点，距离为0
-    // 小顶堆
-    priority_queue<PII, vector<PII>, greater<>> q;
+    dis[1] = 0;
+
+    priority_queue<PII, vector<PII>, greater<int>> q;
     q.push({0, 1});
 
     while (q.size()) {
         PII t = q.top();
         q.pop();
         int u = t.second;
-        if (st[u]) continue; // Dijkstra第一次出队列为最小值
-        st[u] = 1;
+        if (st[u]) continue;
+        st[u] = true;
 
         for (int i = h[u]; ~i; i = ne[i]) {
             int v = e[i];
@@ -51,7 +50,6 @@ int main() {
         cin >> a >> b >> c;
         add(a, b, c), add(b, a, c);
     }
-
     printf("%d\n", dijkstra());
     return 0;
 }

TangDou/AcWing/MinimalPath/1128.md

@@ -56,51 +56,46 @@ $1≤n≤100,1≤m≤200,1≤k≤1000$
 #include <bits/stdc++.h>
 using namespace std;
 typedef pair<int, int> PII;
-
+const int INF = 0x3f3f3f3f;
 const int N = 110;
-const int M = 2 * 210; // 无向边，开两倍
+const int M = 2 * 210; // 无向图，需要开二倍的数组长度！
 
 int n, m;
 int h[N], e[M], w[M], ne[M], idx;
 void add(int a, int b, int c) {
     e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
 }
-int d[N];
+int dis[N];
 bool st[N];
 
 int dijkstra() {
-    int res = 0, cnt = 0;
+    memset(dis, 0x3f, sizeof dis);
+    dis[1] = 0;
 
-    // 初始化为正无穷
-    memset(d, 0x3f, sizeof d);
-    d[1] = 0; // 1号点为出发点，距离为0
-    // 小顶堆
-    priority_queue<PII, vector<PII>, greater<>> q;
+    priority_queue<PII, vector<PII>, greater<int>> q;
     q.push({0, 1});
 
     while (q.size()) {
-        auto u = q.top();
+        PII t = q.top();
         q.pop();
+        int u = t.second;
+        if (st[u]) continue;
+        st[u] = true;
 
-        if (st[u.second]) continue; // Dijkstra第一次出队列为最小值
-        st[u.second] = true;
-
-        // ① 所有最短距离的最大值,就是完成送信的最小时间
-        res = max(res, u.first);
-
-        // ② 记录到达的节点个数
-        cnt++;
-
-        for (int i = h[u.second]; ~i; i = ne[i]) {
+        for (int i = h[u]; ~i; i = ne[i]) {
             int v = e[i];
-            if (d[v] > d[u.second] + w[i]) {
-                d[v] = d[u.second] + w[i];
-                q.push({d[v], v});
+            if (dis[v] > dis[u] + w[i]) {
+                dis[v] = dis[u] + w[i];
+                q.push({dis[v], v});
             }
         }
     }
-    // 如果可以成功到达每个节点，返回最短距离的最大值，否则返回-1
-    return cnt == n ? res : -1;
+    int mx = 0;
+    for (int i = 1; i <= n; i++) {
+        if (dis[i] == INF) return -1;
+        mx = max(mx, dis[i]);
+    }
+    return mx;
 }
 int main() {
     memset(h, -1, sizeof h);
@@ -110,9 +105,7 @@ int main() {
         cin >> a >> b >> c;
         add(a, b, c), add(b, a, c);
     }
-
     printf("%d\n", dijkstra());
     return 0;
 }
-
 ```

TangDou/AcWing/MinimalPath/1129.cpp

@@ -4,46 +4,40 @@ const int N = 2510;
 const int M = 6200 * 2 + 10;
 
 typedef pair<int, int> PII;
-// 邻接表
+
 int h[N], w[M], e[M], ne[M], idx;
-bool st[N]; // 是否使用过
-int d[N];   // 最短距离数组
-// 小顶堆
-priority_queue<PII, vector<PII>, greater<PII>> q;
-int n; // n个城镇
-int m; // m条路径
-int S; // 起点
-int T; // 终点
-
-// 维护邻接表
+bool st[N];
+int dis[N];
+
 void add(int a, int b, int c) {
     e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
 }
 
+int n, m, S, T;
+
 int dijkstra() {
-    memset(d, 0x3f, sizeof d); // 初始化为无穷大
-    d[S] = 0;                  // 出发点的距离初始化为0
-    q.push({0, S});            // 源点入队列
-    // q里装的 first:距离出发点的距离 second:结点编号
+    memset(dis, 0x3f, sizeof dis);
+    dis[S] = 0;
+
+    priority_queue<PII, vector<PII>, greater<PII>> q;
+    q.push({0, S});
     while (q.size()) {
         PII t = q.top();
         q.pop();
         int u = t.second;
-        // 如果此结点已经被尝试过后，而且排在小顶堆的后面被尝试，说明不会更优秀
         if (st[u]) continue;
-        // 用这个点去尝试更新相关的点
         st[u] = true;
         for (int i = h[u]; ~i; i = ne[i]) {
             int v = e[i];
-            if (d[v] > t.first + w[i]) {
-                d[v] = t.first + w[i];
-                q.push({d[v], v});
+            if (dis[v] > dis[u] + w[i]) {
+                dis[v] = dis[u] + w[i];
+                q.push({dis[v], v});
             }
         }
     }
-    return d[T];
+    return dis[T];
 }
-// 30 ms 还是推荐记忆这个，方便，代码短
+
 int main() {
     cin >> n >> m >> S >> T;
     memset(h, -1, sizeof h);

TangDou/AcWing/MinimalPath/1129.md

@@ -45,53 +45,44 @@ $John$已经研究过可以把牛奶从威斯康星运送到德克萨斯州的
 ```cpp {.line-numbers}
 #include <bits/stdc++.h>
 using namespace std;
-/*
-(堆优化dijkstra) O((n+m)logm)
-时间复杂度查了好久，说什么的也有，保险起见，这里就采用那个最高的吧！
- */
 const int N = 2510;
 const int M = 6200 * 2 + 10;
 
 typedef pair<int, int> PII;
-// 邻接表
+
 int h[N], w[M], e[M], ne[M], idx;
-bool st[N]; // 是否使用过
-int d[N];   // 最短距离数组
-// 小顶堆
-priority_queue<PII, vector<PII>, greater<PII>> q;
-int n; // n个城镇
-int m; // m条路径
-int S; // 起点
-int T; // 终点
-
-// 维护邻接表
+bool st[N];
+int dis[N];
+
 void add(int a, int b, int c) {
     e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
 }
 
+int n, m, S, T;
+
 int dijkstra() {
-    memset(d, 0x3f, sizeof d); // 初始化为无穷大
-    d[S] = 0;                  // 出发点的距离初始化为0
-    q.push({0, S});            // 源点入队列
-    // q里装的 first:距离出发点的距离 second:结点编号
+    memset(dis, 0x3f, sizeof dis);
+    dis[S] = 0;
+
+    priority_queue<PII, vector<PII>, greater<PII>> q;
+    q.push({0, S});
     while (q.size()) {
-        PII u = q.top();
+        PII t = q.top();
         q.pop();
-        // 如果此结点已经被尝试过后，而且排在小顶堆的后面被尝试，说明不会更优秀
-        if (st[u.second]) continue;
-        // 用这个点去尝试更新相关的点
-        st[u.second] = true;
-        for (int i = h[u.second]; ~i; i = ne[i]) {
+        int u = t.second;
+        if (st[u]) continue;
+        st[u] = true;
+        for (int i = h[u]; ~i; i = ne[i]) {
             int v = e[i];
-            if (d[v] > u.first + w[i]) {
-                d[v] = u.first + w[i];
-                q.push({d[v], v});
+            if (dis[v] > dis[u] + w[i]) {
+                dis[v] = dis[u] + w[i];
+                q.push({dis[v], v});
             }
         }
     }
-    return d[T];
+    return dis[T];
 }
-// 30 ms 还是推荐记忆这个，方便，代码短
+
 int main() {
     cin >> n >> m >> S >> T;
     memset(h, -1, sizeof h);

TangDou/AcWing/ShortestPath/850.cpp

@@ -6,7 +6,7 @@ const int INF = 0x3f3f3f3f;
 const int N = 150010, M = N << 1;
 
 int st[N];
-int dis[N]; // 距离数组用d,二元组中第一维记为dist,以视区分
+int dis[N]; // 距离数组
 
 // 邻接表
 int e[M], h[N], idx, w[M], ne[M];
@@ -20,23 +20,23 @@ int dijkstra() {
     dis[1] = 0;
     priority_queue<PII, vector<PII>, greater<PII>> q; // 小顶堆
     q.push({0, 1});
+
     while (q.size()) {
         PII t = q.top();
         q.pop();
-        int d = t.first;
         int u = t.second;
         if (!st[u]) {
             st[u] = 1;
             for (int i = h[u]; ~i; i = ne[i]) {
                 int v = e[i];
-                if (dis[v] > d + w[i]) {
-                    dis[v] = d + w[i];
+                if (dis[v] > dis[u] + w[i]) {
+                    dis[v] = dis[u] + w[i];
                     q.push({dis[v], v});
                 }
             }
         }
     }
-    if (dis[n] == INF) return -1; 
+    if (dis[n] == INF) return -1;
     return dis[n];
 }
 int main() {

TangDou/AcWing/ShortestPath/850.md

@@ -32,40 +32,43 @@ $1≤n,m≤1.5×10^5$,图中涉及边长均不小于 $0$，且不超过 $10000$
 #include <bits/stdc++.h>
 
 using namespace std;
+typedef pair<int, int> PII;
 const int INF = 0x3f3f3f3f;
-const int N = 1.5 * 1e5 + 10, M = N;
+const int N = 150010, M = N << 1;
+
 int st[N];
-int d[N]; // 距离数组用d,二元组中第一维记为dist,以视区分
-typedef pair<int, int> PII;
+int dis[N]; // 距离数组
+
 // 邻接表
 int e[M], h[N], idx, w[M], ne[M];
 void add(int a, int b, int c) {
     e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
 }
+
 int n, m;
 int dijkstra() {
-    memset(d, 0x3f, sizeof d);
-    d[1] = 0;
-    priority_queue<PII, vector<PII>, greater<PII>> q;
+    memset(dis, 0x3f, sizeof dis);
+    dis[1] = 0;
+    priority_queue<PII, vector<PII>, greater<PII>> q; // 小顶堆
     q.push({0, 1});
+
     while (q.size()) {
-        auto t = q.top();
+        PII t = q.top();
         q.pop();
-        int dist = t.first;
         int u = t.second;
         if (!st[u]) {
             st[u] = 1;
             for (int i = h[u]; ~i; i = ne[i]) {
                 int v = e[i];
-                if (d[v] > dist + w[i]) {
-                    d[v] = dist + w[i];
-                    q.push({d[v], v});
+                if (dis[v] > dis[u] + w[i]) {
+                    dis[v] = dis[u] + w[i];
+                    q.push({dis[v], v});
                 }
             }
         }
     }
-    if (d[n] == INF) return -1; // 单源最短路
-    return d[n];
+    if (dis[n] == INF) return -1;
+    return dis[n];
 }
 int main() {
     cin >> n >> m;

TangDou/Topic/Mobius/P4318.cpp

@@ -0,0 +1,54 @@
+#include <bits/stdc++.h>
+using namespace std;
+#define int long long
+#define endl "\n"
+const int N = 100010;
+
+// 筛法求莫比乌斯函数(枚举约数)
+int mu[N];
+int primes[N], cnt;
+bool st[N];
+void get_mobius(int n) {
+    mu[1] = 1;
+    for (int i = 2; i <= n; i++) {
+        if (!st[i]) {
+            primes[cnt++] = i;
+            mu[i] = -1;
+        }
+        for (int j = 0; primes[j] <= n / i; j++) {
+            int t = primes[j] * i;
+            st[t] = true;
+            if (i % primes[j] == 0) {
+                mu[t] = 0;
+                break;
+            }
+            mu[t] = -mu[i];
+        }
+    }
+}
+int check(int mid, int k) {
+    int res = 0;
+    for (int i = 1; i * i <= mid; i++) // 枚举范围内每个平方数
+        res += mu[i] * (mid / i / i);
+    return res >= k;
+}
+
+signed main() {
+    // 获取莫比乌斯函数值
+    get_mobius(N - 1);
+
+    int T, k;
+    cin >> T; // T组测试数据
+    while (T--) {
+        cin >> k; // 第k个数
+        int l = 1, r = 2e9;
+        while (l < r) {
+            int mid = l + r >> 1;
+            if (check(mid, k))
+                r = mid;
+            else
+                l = mid + 1;
+        }
+        cout << r << endl;
+    }
+}

TangDou/Topic/Mobius/SQP4168.cpp

@@ -0,0 +1,61 @@
+#include <bits/stdc++.h>
+using namespace std;
+#define int long long
+#define endl "\n"
+const int M = 110;      // 询问次数
+const int N = 10000010; // 莫比乌斯函数值的极限数据上限,sqrt(1e14)=1e7
+int n, sqrtN;           // T次询问，每次都是1~n,sqrtN=sqrt(max(n)),真实上限
+int q[M];               // T次询问，用q数组记录下来
+
+// 筛法求莫比乌斯函数(枚举约数)
+int mu[N], sum[N]; // sum[N]:梅滕斯函数,也就是莫比乌斯函数的前缀和
+int primes[N], cnt;
+bool st[N];
+void get_mobius(int n) {
+    mu[1] = 1;
+    for (int i = 2; i <= n; i++) {
+        if (!st[i]) {
+            primes[cnt++] = i;
+            mu[i] = -1;
+        }
+        for (int j = 0; primes[j] <= n / i; j++) {
+            int t = primes[j] * i;
+            st[t] = true;
+            if (i % primes[j] == 0) {
+                mu[t] = 0;
+                break;
+            }
+            mu[t] = -mu[i];
+        }
+    }
+    // 维护u(x)前缀和:梅滕斯函数
+    for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
+}
+
+signed main() {
+#ifndef ONLINE_JUDGE
+    freopen("SQP4168.in", "r", stdin);
+#endif
+    int T;
+    cin >> T;
+    for (int i = 1; i <= T; i++) {
+        cin >> q[i];
+        n = max(n, q[i]); // 找到最大的n,这样可以避免重复计算
+    }
+    sqrtN = sqrt(n); // 最大的n，只需要枚举到sqrt(n)即可
+    // 对有效范围内的数字求莫比乌斯函数
+    get_mobius(sqrtN); // 线性求莫比乌斯函数, 前缀和
+
+    for (int i = 1; i <= T; i++) {              // 离线处理，对于每个询问进行回答
+        n = q[i];                               // 第i次的n值
+        int ans = 0;                            // 初始化返回结果
+        for (int l = 1, r; l <= n; l = r + 1) { // 整除分块
+            if (n / (l * l) == 0) break;
+            // n / (l * l): 分块的左边界是l,值是n/(l*l),如果n<(l*l)时，l再长大也没用，也都是0
+            // n/(l*l):整除分块中整个分块内的个数值，从n/(l*l)~n/(r*r)是同一个值
+            r = sqrt(n / (n / (l * l)));                // 求出右边界r
+            ans += n / (l * l) * (sum[r] - sum[l - 1]); // 利用莫比乌斯函数值前缀和求块的贡献
+        }
+        cout << ans << endl;
+    }
+}

TangDou/Topic/Mobius/SQP4168.in

@@ -0,0 +1,4 @@
+3
+1
+1000
+100000000000000

TangDou/Topic/Mobius/mobius.cpp

@@ -0,0 +1,82 @@
+#include <bits/stdc++.h>
+
+using namespace std;
+#define int long long
+#define endl "\n"
+
+const int N = 1e5 + 10;
+int n = 20;
+
+// 筛法求莫比乌斯函数(枚举约数)
+int mu[N], sum[N]; // sum[N]:梅滕斯函数,也就是莫比乌斯函数的前缀和
+int primes[N], cnt;
+bool st[N];
+void get_mobius(int n) {
+    mu[1] = 1;
+    for (int i = 2; i <= n; i++) {
+        if (!st[i]) {
+            primes[cnt++] = i;
+            mu[i] = -1;
+        }
+        for (int j = 0; primes[j] <= n / i; j++) {
+            int t = primes[j] * i;
+            st[t] = true;
+            if (i % primes[j] == 0) {
+                mu[t] = 0;
+                break;
+            }
+            mu[t] = -mu[i];
+        }
+    }
+    // 维护u(x)前缀和:梅滕斯函数
+    for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
+}
+
+// 最简筛法求莫比乌斯函数(枚举倍数)
+void get_mobius_beishu(int x) {
+    mu[1] = 1;
+    for (int i = 1; i <= x; i++)
+        for (int j = i + i; j <= x; j += i)
+            mu[j] -= mu[i];
+}
+
+// 单个数的莫比乌斯函数
+int getmob(int x) {
+    int sum = 0;
+    for (int i = 2; i <= x / i; i++) { // 从2开始，一直到 sqrt(x),枚举所有可能存的小因子
+        int cnt = 0;
+        if (x % i == 0) {                     // 如果x可以整除i
+            while (x % i == 0) cnt++, x /= i; // 计数，并且不断除掉这个i因子
+            if (cnt > 1) return 0;            // 如果某个因子，存在两个及以上个，则返回0
+            sum++;                            // 记录因子个数
+        }
+    }
+    if (x != 1) sum++;         // 如果还存在另一个大因子，那么因子个数+1
+    return (sum & 1) ? -1 : 1; // 奇数个因子，返回-1,否则返回1
+}
+
+void printIdx(int n) {
+    for (int i = 1; i <= n; i++) printf("%2lld ", i);
+    cout << endl;
+}
+
+signed main() {
+    // 计算单个数字的莫比乌斯函数
+    for (int i = 1; i <= n; i++) printf("%2lld ", getmob(i));
+    cout << endl;
+
+    // 枚举约数的筛法
+    get_mobius(n);
+    for (int i = 1; i <= n; i++) printf("%2lld ", mu[i]);
+    cout << endl;
+
+    // 清空一下，继续测试
+    memset(mu, 0, sizeof mu);
+
+    // 枚举倍数的筛法
+    get_mobius_beishu(n);
+    for (int i = 1; i <= n; i++) printf("%2lld ", mu[i]);
+    cout << endl;
+
+    printIdx(n);
+}

TangDou/Topic/Mobius/mobius_Prepare.cpp

@@ -0,0 +1,21 @@
+#include <bits/stdc++.h>
+using namespace std;
+int main() {
+    // 讨论F(i)与f(i)的所有因子之间的关联关系
+    int n = 100;
+    for (int i = 1; i <= n; i++) {
+        printf("F(%d)=", i);
+        bool f = 1;
+        for (int j = 1; j <= n; j++) {
+            if (i % j == 0) { // 如果j是i的因子的话，输出f(j)
+                if (f) {
+                    printf("f(%d)", j);
+                    f = 0;
+                } else
+                    printf("+f(%d)", j);
+            }
+        }
+        printf("\n");
+    }
+    return 0;
+}

TangDou/Topic/PrefixAndSuffix/P1083.cpp

@@ -0,0 +1,41 @@
+#include <bits/stdc++.h>
+using namespace std;
+const int N = 1000010;
+#define int long long
+#define endl "\n"
+int n, m;                   // 天数和订单的数量
+int r[N];                   // 第i天学校有r[i]个教室可借用
+int d[N], s[N], t[N];       // 借的教室数目、从第s天借到t天
+int b[N];                   // 差分数组
+bool check(int x) {         // 判断能不能通过x个人
+    memset(b, 0, sizeof b); // 每次判断都要先初始化差分数组
+    int sum = 0;            // 记录需要借的教室数
+    for (int i = 1; i <= x; i++) {
+        b[s[i]] += d[i];     // 因为只会对在s~l之间要借用教室的人产生影响，所以可以差分
+        b[t[i] + 1] -= d[i]; // 差分,注意:是t[i]+1，因为要包含t[i]这个点
+    }
+    for (int i = 1; i <= n; i++) {
+        sum += b[i];                  // 因为cf是差分数组，所以sum就是在第i天的借教室的总数
+        if (sum > r[i]) return false; // 不可行，如果要借的教室多于空的教室
+    }
+    return true; // 可行
+}
+signed main() {
+    cin >> n >> m;
+    for (int i = 1; i <= n; i++) cin >> r[i];
+    for (int i = 1; i <= m; i++) cin >> d[i] >> s[i] >> t[i];
+    if (check(m)) {        // 如果全部满足
+        cout << 0 << endl; // 输出0
+        exit(0);           // 直接结束程序
+    }
+    int l = 1, r = m; // 二分左右区间
+    while (l < r) {
+        int mid = l + r >> 1;
+        if (check(mid))  // 如果可行
+            l = mid + 1; // 增多满足人数
+        else             // 否则
+            r = mid;     // 减少满足人数
+    }
+    cout << "-1" << endl
+         << l; // 输出-1和需要修改的人
+}

TangDou/Topic/PrefixAndSuffix/P1083_0.cpp

@@ -0,0 +1,28 @@
+#include <bits/stdc++.h>
+using namespace std;
+int n, m;
+const int N = 1000010;
+int r[N];
+int main() {
+    cin >> n >> m;
+    // 每一天可租借教室数
+    for (int i = 1; i <= n; i++) cin >> r[i];
+
+    // 从哪天到哪天，借多少个
+    for (int i = 1; i <= m; i++) {
+        int d, s, t;
+        cin >> d >> s >> t;
+        // 从开始天到结束天
+        for (int j = s; j <= t; j++) {
+            r[j] -= d;      // 减去借走的教室数
+            if (r[j] < 0) { // 小于0了！
+                cout << -1 << endl
+                     << i << endl;
+                return 0;
+            }
+        }
+    }
+
+    cout << 0 << endl;
+    return 0;
+}

TangDou/Topic/PrefixAndSuffix/P1115.cpp

@@ -0,0 +1,21 @@
+#include <bits/stdc++.h>
+using namespace std;
+const int N = 1e6 + 10;
+const int INF = 0x3f3f3f3f;
+int n, a[N], s[N], ans[N];
+
+int main() {
+    cin >> n;
+    for (int i = 1; i <= n; i++)
+        cin >> a[i], s[i] = s[i - 1] + a[i]; // 前缀和
+
+    int mi = 0;
+    for (int i = 1; i <= n; i++) {
+        ans[i] = s[i] - mi;
+        mi = min(mi, s[i]);
+    }
+    int res = -INF;
+    for (int i = 1; i <= n; i++) res = max(res, ans[i]);
+    cout << res << endl;
+    return 0;
+}

TangDou/Topic/PrefixAndSuffix/P3397.cpp

@@ -0,0 +1,28 @@
+#include <bits/stdc++.h>
+using namespace std;
+
+const int N = 1010;
+int b[N][N], s[N][N];
+int n, m;
+
+int main() {
+    cin >> n >> m;
+    while (m--) {
+        // 从0开始构建差分数组
+        int x1, y1, x2, y2;
+        cin >> x1 >> y1 >> x2 >> y2;
+        b[x1][y1] += 1; // 进行子矩阵的加减，差分
+        b[x2 + 1][y1] -= 1;
+        b[x1][y2 + 1] -= 1;
+        b[x2 + 1][y2 + 1] += 1;
+    }
+    // 还原为原始数组
+    for (int i = 1; i <= n; i++) {
+        for (int j = 1; j <= n; j++) {
+            s[i][j] = b[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1]; // 把之前的加减结果进行求和
+            printf("%d ", s[i][j]);                                          // 注意输出格式，每个数带一个空格
+        }
+        printf("\n"); // 结束一行的输出输出一个换行符号
+    }
+    return 0;
+}

TangDou/Topic/PrefixAndSuffix/P3406.cpp

@@ -0,0 +1,35 @@
+#include <bits/stdc++.h>
+using namespace std;
+#define int long long
+#define endl "\n"
+const int N = 100010;
+int n, m;             // 铁路途经n个城市，要去m个城市
+int p[N];             // 记录经过站点的顺序
+int a[N], b[N], c[N]; // 记录每段路径所花的费用
+int t[N];             // 记录站点之间的路径经过的次数
+int ans;              // 答案
+signed main() {
+    cin >> n >> m;
+
+    for (int i = 1; i <= m; i++) cin >> p[i];
+    for (int i = 1; i < n; i++) cin >> a[i] >> b[i] >> c[i];
+
+    // 所有的区间都以较小的点排在前面，例如：2-1，5-3都用1-2，3-5表示，
+    // 且每一段都用前面较小的点作为标记！！！！
+    for (int i = 1; i < m; i++) {
+        int x, y;
+        if (p[i] > p[i + 1]) {
+            x = p[i + 1];
+            y = p[i];
+        } else {
+            x = p[i];
+            y = p[i + 1];
+        }
+        t[x]++;
+        t[y]--;
+    }
+    for (int i = 1; i <= n; i++) t[i] += t[i - 1]; // 求前缀和
+    for (int i = 1; i <= n - 1; i++)
+        ans += min(a[i] * t[i], (b[i] * t[i] + c[i])); // 求总的最小就是把每一段的最小相加
+    cout << ans << endl;
+}

TangDou/Topic/mobius.cpp

@@ -1,81 +0,0 @@
-#include <bits/stdc++.h>
-
-using namespace std;
-
-typedef long long LL;
-const int N = 1e5 + 10;
-int n = 20;
-
-// 筛法求莫比乌斯函数(枚举约数)
-LL mu[N], sum[N];
-int primes[N], cnt;
-bool st[N];
-void get_mobius2(LL n) {
-    mu[1] = 1;
-    for (LL i = 2; i <= n; i++) {
-        if (!st[i]) {
-            primes[cnt++] = i;
-            mu[i] = -1;
-        }
-        for (LL j = 0; primes[j] <= n / i; j++) {
-            LL t = primes[j] * i;
-            st[t] = true;
-            if (i % primes[j] == 0) {
-                mu[t] = 0;
-                break;
-            }
-            mu[t] = mu[i] * -1;
-        }
-    }
-    // 维护u(x)前缀和
-    for (LL i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
-}
-
-// 最简筛法求莫比乌斯函数(枚举倍数)
-void get_mobius1(LL x) {
-    mu[1] = 1;
-    for (LL i = 1; i <= x; i++)
-        for (LL j = i + i; j <= x; j += i)
-            mu[j] -= mu[i];
-}
-
-// 单个数的莫比乌斯函数
-int getmob(LL x) {
-    int sum = 0;
-    for (LL i = 2; i <= x / i; i++) { // 从2开始，一直到 sqrt(x),枚举所有可能存的小因子
-        int cnt = 0;
-        if (x % i == 0) {                     // 如果x可以整除i
-            while (x % i == 0) cnt++, x /= i; // 计数，并且不断除掉这个i因子
-            if (cnt > 1) return 0;            // 如果某个因子，存在两个及以上个，则返回0
-            sum++;                            // 记录因子个数
-        }
-    }
-    if (x != 1) sum++;         // 如果还存在另一个大因子，那么因子个数+1
-    return (sum & 1) ? -1 : 1; // 奇数个因子，返回-1,否则返回1
-}
-
-int main() {
-    // 计算单个数字的莫比乌斯函数
-    for (int i = 1; i <= n; i++) printf("%2d ", getmob(i));
-    cout << endl;
-    for (int i = 1; i <= n; i++) printf("%2d ", i);
-
-    // 筛法求莫比乌斯函数
-    // get_mobius1(n);
-    // for (int i = 1; i <= n; i++)
-    //     cout << "mu1[" << i << "]=" << mu[i] << endl;
-
-    // //清空一下，继续测试
-    // memset(mu, 0, sizeof mu);
-
-    // //测试枚举约数的筛法
-    // get_mobius2(n);
-
-    // for (int i = 1; i <= n; i++) {
-    //     //计算单个数字的莫比乌斯函数
-    //     cout << "mu2[" << i << "]=" << getmob(i) << endl;
-    //     cout << "mu2[" << i << "]=" << mu[i] << endl;
-    //     cout << "========================================" << endl;
-    // }
-    return 0;
-}

TangDou/Topic/【最短路径】Dijkstra算法专题.md

@@ -0,0 +1,202 @@
+## $Dijkstra$算法专题
+
+### 一、解决的问题
+计算从 **源** 到所有其他各顶点的最短路径长度。这里的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。
+
+### 二、算法原理
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312180745532.png)
+
+> **视频讲解** : **[【5分钟搞定$Dijkstra$算法】](https://www.bilibili.com/video/BV1ha4y1T7om)**
+
+### 三、题单
+#### 【模板题】[$AcWing$ $850$. $Dijkstra$求最短路 $II$](https://www.acwing.com/problem/content/description/852/) 
+
+输入样例
+```cpp {.line-numbers}
+3 3
+1 2 2
+2 3 1
+1 3 4
+```
+输出样例
+```cpp {.line-numbers}
+3
+```
+**$Code$**
+```cpp {.line-numbers}
+#include <bits/stdc++.h>
+
+using namespace std;
+typedef pair<int, int> PII;
+const int INF = 0x3f3f3f3f;
+const int N = 150010, M = N << 1;
+
+int st[N];
+int dis[N]; // 距离数组
+
+// 邻接表
+int e[M], h[N], idx, w[M], ne[M];
+void add(int a, int b, int c) {
+    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
+}
+
+int n, m;
+int dijkstra() {
+    memset(dis, 0x3f, sizeof dis);
+    dis[1] = 0;
+    priority_queue<PII, vector<PII>, greater<PII>> q; // 小顶堆
+    q.push({0, 1});
+
+    while (q.size()) {
+        PII t = q.top();
+        q.pop();
+        int u = t.second;
+        if (!st[u]) {
+            st[u] = 1;
+            for (int i = h[u]; ~i; i = ne[i]) {
+                int v = e[i];
+                if (dis[v] > dis[u] + w[i]) {
+                    dis[v] = dis[u] + w[i];
+                    q.push({dis[v], v});
+                }
+            }
+        }
+    }
+    if (dis[n] == INF) return -1;
+    return dis[n];
+}
+int main() {
+    cin >> n >> m;
+    memset(h, -1, sizeof h);
+    while (m--) {
+        int a, b, c;
+        cin >> a >> b >> c;
+        add(a, b, c);
+    }
+    printf("%d\n", dijkstra());
+    return 0;
+}
+```
+
+### [$AcWing$ $1129$. 热浪](https://www.acwing.com/problem/content/description/1131/)
+与模板相比，只是起点和终点是输入的，其它无区别。
+
+**$Code$**
+```cpp {.line-numbers}
+#include <bits/stdc++.h>
+using namespace std;
+const int N = 2510;
+const int M = 6200 * 2 + 10;
+
+typedef pair<int, int> PII;
+
+int h[N], w[M], e[M], ne[M], idx;
+bool st[N];
+int dis[N];
+
+void add(int a, int b, int c) {
+    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
+}
+
+int n, m, S, T;
+
+int dijkstra() {
+    memset(dis, 0x3f, sizeof dis);
+    dis[S] = 0;
+
+    priority_queue<PII, vector<PII>, greater<PII>> q;
+    q.push({0, S});
+    while (q.size()) {
+        PII t = q.top();
+        q.pop();
+        int u = t.second;
+        if (st[u]) continue;
+        st[u] = true;
+        for (int i = h[u]; ~i; i = ne[i]) {
+            int v = e[i];
+            if (dis[v] > dis[u] + w[i]) {
+                dis[v] = dis[u] + w[i];
+                q.push({dis[v], v});
+            }
+        }
+    }
+    return dis[T];
+}
+
+int main() {
+    cin >> n >> m >> S >> T;
+    memset(h, -1, sizeof h);
+
+    while (m--) {
+        int a, b, c;
+        cin >> a >> b >> c;
+        add(a, b, c), add(b, a, c);
+    }
+    printf("%d\n", dijkstra());
+    return 0;
+}
+```
+
+#### [$AcWing$ $1128$. 信使](https://www.acwing.com/problem/content/1130/)
+**总结**：从$1$号哨所出发，计算出到每个哨所的最短路径，所以最短路径中最长的，表示需要的最少时间，是一个最短路径模板+思维问题。
+
+**$Code$**
+
+```cpp {.line-numbers}
+#include <bits/stdc++.h>
+using namespace std;
+typedef pair<int, int> PII;
+const int INF = 0x3f3f3f3f;
+const int N = 110;
+const int M = 2 * 210; // 无向图，需要开二倍的数组长度！
+
+int n, m;
+int h[N], e[M], w[M], ne[M], idx;
+void add(int a, int b, int c) {
+    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
+}
+int dis[N];
+bool st[N];
+
+int dijkstra() {
+    memset(dis, 0x3f, sizeof dis);
+    dis[1] = 0;
+
+    priority_queue<PII, vector<PII>, greater<int>> q;
+    q.push({0, 1});
+
+    while (q.size()) {
+        PII t = q.top();
+        q.pop();
+        int u = t.second;
+        if (st[u]) continue;
+        st[u] = true;
+
+        for (int i = h[u]; ~i; i = ne[i]) {
+            int v = e[i];
+            if (dis[v] > dis[u] + w[i]) {
+                dis[v] = dis[u] + w[i];
+                q.push({dis[v], v});
+            }
+        }
+    }
+    int mx = 0;
+    for (int i = 1; i <= n; i++) {
+        if (dis[i] == INF) return -1;
+        mx = max(mx, dis[i]);
+    }
+    return mx;
+}
+int main() {
+    memset(h, -1, sizeof h);
+    cin >> n >> m;
+    while (m--) {
+        int a, b, c;
+        cin >> a >> b >> c;
+        add(a, b, c), add(b, a, c);
+    }
+    printf("%d\n", dijkstra());
+    return 0;
+}
+
+```

TangDou/Topic/前缀和和差分洛谷题单总结.md

@@ -0,0 +1,195 @@
+## 前缀和和差分洛谷题单总结
+
+[参考文献](https://blog.csdn.net/piqihaoshaonian/article/details/127515000)
+
+### 一、公式
+#### 前缀和的公式
+一维：$s[i] = a[i] + s[i-1]$
+
+二维：$s[i][j] = a[i][j] + s[i-1] [j] + s[ i] [j-1] - s[i-1][j-1]$
+
+#### 差分的公式
+一维：$b[i] =s[i] - s[i-1]$
+
+二维：$b[i] = s[i][j] - s[i-1][j]-s[i][j-1]+s[i-1][j-1]$
+
+### 二、题单
+#### [$P1115$ 最大子段和](https://www.luogu.com.cn/problem/P1115)
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170827397.png)
+
+**分析**
+先求每个位置的前缀和（某个区间求和前缀和可以说是最快的），然后去找该位置前前缀和的最小值，如果要求一段和最大，就要用这段和减去前面最小的值。
+
+```cpp {.line-numbers}
+#include <bits/stdc++.h>
+using namespace std;
+const int N = 1e6 + 10;
+const int INF = 0x3f3f3f3f;
+int n, a[N], s[N], ans[N];
+
+int main() {
+    cin >> n;
+    for (int i = 1; i <= n; i++)
+        cin >> a[i], s[i] = s[i - 1] + a[i]; // 前缀和
+
+    int mi = 0;
+    for (int i = 1; i <= n; i++) {
+        ans[i] = s[i] - mi;
+        mi = min(mi, s[i]);
+    }
+    int res = -INF;
+    for (int i = 1; i <= n; i++) res = max(res, ans[i]);
+    cout << res << endl;
+    return 0;
+}
+```
+
+#### [$P3397$ 地毯](https://www.luogu.com.cn/problem/P3397)
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170847131.png)
+
+**分析**
+看到这里的时候，我就想到了一个矩阵的某个子矩阵进行加减，瞬间想到二维差分和二位前缀和,二位差分的公式为：
+
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170848375.png)
+
+由差分算的二位前缀和公式：
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170849629.png)
+
+```cpp {.line-numbers}
+#include <bits/stdc++.h>
+using namespace std;
+
+const int N = 1010;
+int b[N][N], s[N][N];
+int n, m;
+
+int main() {
+    cin >> n >> m;
+    while (m--) {
+        // 从0开始构建差分数组
+        int x1, y1, x2, y2;
+        cin >> x1 >> y1 >> x2 >> y2;
+        b[x1][y1] += 1; // 进行子矩阵的加减，差分
+        b[x2 + 1][y1] -= 1;
+        b[x1][y2 + 1] -= 1;
+        b[x2 + 1][y2 + 1] += 1;
+    }
+    // 还原为原始数组
+    for (int i = 1; i <= n; i++) {
+        for (int j = 1; j <= n; j++) {
+            s[i][j] = b[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1]; // 把之前的加减结果进行求和
+            printf("%d ", s[i][j]);                                          // 注意输出格式，每个数带一个空格
+        }
+        printf("\n"); // 结束一行的输出输出一个换行符号
+    }
+    return 0;
+}
+```
+### [$P1083$ [$NOIP2012$ 提高组] 借教室](https://www.luogu.com.cn/problem/P1083)
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170927931.png)
+
+#### 暴力
+还是先看暴力怎么做吧，对于$m$次借教室，我们可以每次把区间$s\sim t$的空教室数$r-=d$，当有一次$r<0$时，则当前这个人无法被满足，直接输出$-1$和当前这个人的号数，然后直接结束程序。如果$m$次借教室都操作完成后依然没有房间数$r<0$，则说明所有人都可以被满足，则输出$0$。
+
+综合上述做法，得分$60$。
+
+```cpp {.line-numbers}
+#include <bits/stdc++.h>
+using namespace std;
+int n, m;
+const int N = 1000010;
+int r[N];
+int main() {
+    cin >> n >> m;
+    // 每一天可租借教室数
+    for (int i = 1; i <= n; i++) cin >> r[i];
+
+    // 从哪天到哪天，借多少个
+    for (int i = 1; i <= m; i++) {
+        int d, s, t;
+        cin >> d >> s >> t;
+        // 从开始天到结束天
+        for (int j = s; j <= t; j++) {
+            r[j] -= d;      // 减去借走的教室数
+            if (r[j] < 0) { // 小于0了！
+                cout << -1 << endl
+                     << i << endl;
+                return 0;
+            }
+        }
+    }
+
+    cout << 0 << endl;
+    return 0;
+}
+```
+显然，这样做法的时间复杂度时$O(N*M)$的，无法通过此题，从而我们可以推知该题正确的时间复杂度应该是$log$级的。
+
+#### 正解
+既然时间复杂度时$log$级的，于是想到了二分。
+
+再看到每个人借教室的时间可以看成一个区间，且该区间只会对其他在该区间要借教室的人产生影响，对于区间之外的借教室的人是不会产生影响的，于是又想到了差分。
+
+差分序列：（可用于区间增减）记录相邻两个量的变化量，所以当在一段区间$[l,r]$上增加$a$时，只需要在$l$处加$a$，在$r+1$处$-a$即可。
+
+对于为什么可以二分：如果一个人无法被满足，则他后面的人全都不能被满足；如果一个人可以被满足，则他前面的人都可以被满足,这恰恰吻合了我们二分的性质。
+
+```cpp {.line-numbers}
+#include <bits/stdc++.h>
+using namespace std;
+const int N = 1000010;
+#define int long long
+#define endl "\n"
+int n, m;                   // 天数和订单的数量
+int r[N];                   // 第i天学校有r[i]个教室可借用
+int d[N], s[N], t[N];       // 借的教室数目、从第s天借到t天
+int b[N];                   // 差分数组
+bool check(int x) {         // 判断能不能通过x个人
+    memset(b, 0, sizeof b); // 每次判断都要先初始化差分数组
+    int sum = 0;            // 记录需要借的教室数
+    for (int i = 1; i <= x; i++) {
+        b[s[i]] += d[i];     // 因为只会对在s~l之间要借用教室的人产生影响，所以可以差分
+        b[t[i] + 1] -= d[i]; // 差分,注意:是t[i]+1，因为要包含t[i]这个点
+    }
+    for (int i = 1; i <= n; i++) {
+        sum += b[i];                  // 因为cf是差分数组，所以sum就是在第i天的借教室的总数
+        if (sum > r[i]) return false; // 不可行，如果要借的教室多于空的教室
+    }
+    return true; // 可行
+}
+signed main() {
+    cin >> n >> m;
+    for (int i = 1; i <= n; i++) cin >> r[i];
+    for (int i = 1; i <= m; i++) cin >> d[i] >> s[i] >> t[i];
+    if (check(m)) {        // 如果全部满足
+        cout << 0 << endl; // 输出0
+        exit(0);           // 直接结束程序
+    }
+    int l = 1, r = m; // 二分左右区间
+    while (l < r) {
+        int mid = l + r >> 1;
+        if (check(mid))  // 如果可行
+            l = mid + 1; // 增多满足人数
+        else             // 否则
+            r = mid;     // 减少满足人数
+    }
+    cout << "-1" << endl
+         << l; // 输出-1和需要修改的人
+}
+```
+
+### [$P3406$ 海底高铁](https://www.luogu.com.cn/problem/P3406)
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170857701.png)
+
+**分析**
+① 每一段的最小费用加起来则总体费用最小。
+
+② 这里的区间是线段而不是一个具体的数，所以我们需要以一个统一的标准进行区间段的区分：于是我们想到了以每个区间的左端点值进行整个线段的记录。
+
+③ 节约时间可以对某段区间做同样的加减数的方法：想到的就是差分（当然有差分就会有由差分求前缀和）。
+
+④ 最后用得到的线段数比较两种购买方案。
+
+
+**注意**
+当然代码中还有很多需要记录的细节！！！例如：线段数是站点数-1，同时差分和前缀和的循环最好是从1开始（涉及边界问题）

TangDou/Topic/莫比乌斯函数.md

@@ -1,3 +1,4 @@
+
 ## 莫比乌斯函数
 
 **[【数论】为什么莫比乌斯函数长这样？这样理解最自然！](https://www.bilibili.com/video/BV165411G7v3)**
@@ -6,39 +7,14 @@
 
 https://blog.csdn.net/qq_49593247/article/details/120394226
 
-https://www.cnblogs.com/letlifestop/p/10262757.html
-
-// https://blog.csdn.net/qq_42887171/article/details/95237740
+### 一、莫比乌斯函数
 
-要学习莫比乌斯函数需要学习 到 **积性函数**，深度理解 **欧拉筛** 。
+先明确一点，莫比乌斯函数并不是什么很高大上的东西，它其实只是一个由容斥系数所构成的函数。
 
-### 一、积性函数
+**[视频讲解：两分钟学会墨比乌斯函数](https://www.bilibili.com/video/BV12P4y1Q7tc/)**
 
 #### 1. 定义
 
-**积性函数**：若$gcd(a,b)=1$，且满足$f(a*b)=f(a)*f(b)$，则称$f(x)$为 **积性函数**
-
-**完全积性函数**：对于任意正整数$a，b$，都满足$f(a*b)=f(a)*f(b)$，则称$f(x)$为 **完全积性函数**
-
-#### 2. 性质
-
-1. 若$f(n),g(n)$均为积性函数，则函数$h(n)=f(n)*g(n)$也是积性函数
-
-2. 若$f(n)$为积性函数，则函数$c*f(n)$($c$是常数)也是积性函数，反之一样
-
-3. **任何积性函数都能应用线性筛**，在$O(n)$时间内求出$1\sim n$项(**莫比乌斯函数要用到**)，像素数，欧拉函数等都是 **积性函数**。
-
-
-### 二、莫比乌斯函数
-
-#### 1. 用途
-
-我们举例一道经典的应用题，求$1$到$N$中与$a$互质的数的个数：根据容斥原理，设$S_i$为$1$到$N$中和$a$有公因子$i$的数的个数，答案为$N−S_2-S_3-S_5-S_7...+S_{2,3}+S_{3,5}+S_{2,5}...$,可以发现，其答案为$\large \displaystyle \sum_{i=1}^{N}\mu(i)*S_i$。
-
-> **注**：在使用容斥原理解决计数问题时，莫比乌斯函数的值就是每一项的系数，要么是$1$，要么是$-1$。这是因为莫比乌斯函数在容斥原理中的作用就是用来表示每个子集合的权重，从而在计算中起到排除重复计数的作用。
-
-#### 2. 定义
-
 ![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312151650942.png)
 
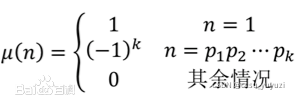
 莫比乌斯函数是个分段函数,它的意思:
@@ -55,169 +31,247 @@ https://www.cnblogs.com/letlifestop/p/10262757.html
 函数值 1 -1 -1  0 -1  1 -1  0  0  1 -1  0 -1  1  1  0 -1  0 -1  0 
 数 字: 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
 ```
+
+#### 2. 用途
+
+我们举例一道经典的应用题，求$1$到$N$中与$a$互质的数的个数：根据容斥原理，设$S_i$为$1$到$N$中和$a$有公因子$i$的数的个数，答案为$N−S_2-S_3-S_5-S_7...+S_{2,3}+S_{3,5}+S_{2,5}...$,可以发现，其答案为$\large \displaystyle \sum_{i=1}^{N}\mu(i)*S_i$。
+
+> **注**：在使用容斥原理解决计数问题时，莫比乌斯函数的值就是每一项的系数，要么是$1$，要么是$-1$。这是因为莫比乌斯函数在容斥原理中的作用就是用来表示每个子集合的权重，从而在计算中起到排除重复计数的作用。
+
+
 #### 3. 求单个数字的莫比乌斯函数值
 
 ```cpp {.line-numbers}
-//单个数的莫比乌斯函数
-int getmob(LL x) {
+// 单个数的莫比乌斯函数
+int getmob(int x) {
     int sum = 0;
-    for (LL i = 2; i <= x / i; i++) { //从2开始，一直到 sqrt(x),枚举所有可能存的小因子
+    for (int i = 2; i <= x / i; i++) { // 从2开始，一直到 sqrt(x),枚举所有可能存的小因子
         int cnt = 0;
-        if (x % i == 0) {                     //如果x可以整除i
-            while (x % i == 0) cnt++, x /= i; //计数，并且不断除掉这个i因子
-            if (cnt > 1) return 0;            //如果某个因子，存在两个及以上个，则返回0
-            sum++;                            //记录因子个数
+        if (x % i == 0) {                     // 如果x可以整除i
+            while (x % i == 0) cnt++, x /= i; // 计数，并且不断除掉这个i因子
+            if (cnt > 1) return 0;            // 如果某个因子，存在两个及以上个，则返回0
+            sum++;                            // 记录因子个数
         }
     }
-    if (x != 1) sum++;         //如果还存在另一个大因子，那么因子个数+1
-    return (sum & 1) ? -1 : 1; //奇数个因子，返回-1,否则返回1
+    if (x != 1) sum++;         // 如果还存在另一个大因子，那么因子个数+1
+    return (sum & 1) ? -1 : 1; // 奇数个因子，返回-1,否则返回1
 }
 ```
 
-#### 4.枚举倍数求莫比乌斯函数(埃氏筛)
-```cpp {.line-numbers}
-//枚举倍数求莫比乌斯函数
-LL mu[N] , sum[N];
-void mobius(LL x) {
-    mu[1] = 1;
-    for (LL i = 1; i <= x; i++)
-        for (LL j = i + i; j <= x; j += i)
-            mu[j] -= mu[i];
-    // 维护u(x)前缀和
-    for (LL i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
-}
-```
-
-
-#### 5.枚举约数求莫比乌斯函数(欧拉筛)
+#### 4.欧拉筛扩展求莫比乌斯函数
 **[视频讲解](https://www.bilibili.com/video/BV1Te4y1C7DP)**
 
 ```cpp {.line-numbers}
-LL mu[N] , sum[N];
+// 筛法求莫比乌斯函数(枚举约数)
+int mu[N], sum[N]; // sum[N]:梅滕斯函数,也就是莫比乌斯函数的前缀和
 int primes[N], cnt;
 bool st[N];
-void get_mobius2(LL n) {
+void get_mobius(int n) {
     mu[1] = 1;
-    for (LL i = 2; i <= n; i++) {
+    for (int i = 2; i <= n; i++) {
         if (!st[i]) {
             primes[cnt++] = i;
             mu[i] = -1;
         }
-        for (LL j = 0; primes[j] <= n / i; j++) {
-            LL t = primes[j] * i;
+        for (int j = 0; primes[j] <= n / i; j++) {
+            int t = primes[j] * i;
             st[t] = true;
             if (i % primes[j] == 0) {
                 mu[t] = 0;
                 break;
             }
-            mu[t] = mu[i] * -1;
+            mu[t] = -mu[i];
         }
     }
-     // 维护u(x)前缀和
-    for (LL i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
+    // 维护u(x)前缀和:梅滕斯函数
+    for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
 }
 ```
 
-#### 6、性质$I$
-![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312151706885.png)
 
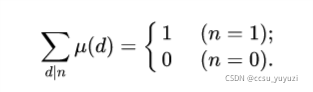
-该图意为$n$的所有因子的莫比乌斯值的和只有在$n=1$时成立为$1$,其余通通为$0$;
+### 二、题单
+**[$SP4168$ $SQFREE$ - $Square$-$free$ $integers$](https://www.luogu.com.cn/problem/SP4168)**
 
-对这个性质的证明:
+**题意**
+在数论中，如果一个整数不能被任何一个整数（这个整数不是$1$）的平方整除，我们就称它是一个$Square−freeinteger$（**无平方数因数的数**）。你得数一数!
 
-首先我们可以把$n$分解为很多个质数相乘(此时质数的幂不一定为$1$):
-令 $\large n=p_1^ {a_1}* p_2^ {a_2}* ... *p_k^{a_k}$
+求出$1 \sim n$ 中无平方因子数的个数。
 
-$\displaystyle \sum_{d | n} \mu(d)$ 这是求$n$的所有约数的莫比乌斯函数值的和,相当于在$p_1,p_2,p_3,...$这些素数中选择若干个质因子相乘来组成所有约数。
+**题解**
 
-根据莫比乌斯函数性质,包含有素数平方的约数不用计算,他对答案的贡献值为$0$,所以我们可以把$n$分解的质数的次数全部消除为$1$,只有当莫比乌斯值为$-1$或者$1$时才对结果有贡献.那么问题就单纯的变为在$k$个$n$的质因子中选$0$到$k$个值组成约数,再将这些约数的值相加:
+先来求一下 **平方数因数** 的数有多少个：
 
-![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312151710689.png)
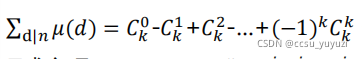
+在$[1, n]$ 中，有多少个数是$x^2$的倍数? 显然是$⌊\frac{n}{x^2}⌋$个。
 
-注意,这里的符号并不是全为加法,而是隔一个加隔一个减,这是因为莫比乌斯函数是积性函数,当选的数是奇数个时为值为负,反之为正,又因二项式定理,将$-1$和$1$带入,可以得到结果为$0$.
+那 $⌊\frac{n}{x^2}⌋$ 就是答案了吗？当然不是，有大量的数被重复计算了。
 
+例如 $36$，它等于$2^2\times 3^2$ ，在计算 $2$ 和 $3$ 的时候它会被重复计算。
 
+怎么办呢？
 
-#### 7、性质$II$
-对任意正整数$n$
-![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312151712295.png)
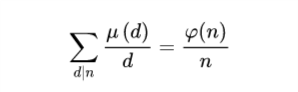
+利用容斥思想，$1$到$n$以内有平方因数的数有$\large \frac{n}{2^2}+\frac{n}{3^2}+\frac{n}{5^2}-\frac{n}{6^2}...$。
+> **注**：
+> ① 为什么没有$4^2,8^2$呢？这是因为$4^2=4 \times 2^2,8^2=16\times 2^2$,在计算$2^2$的个数时，已经计算过了，同理，合数都可以拆分成质数的乘积，我们只要计算质数的平方就可以了。
+② 但是 $6^2=2^2\times 3^2$这样的数字比较特殊，它会被在计算$2^2$时计算一遍，在计算$3^2$时又计算了一遍，计算重复了，需要再扣除掉$\frac{n}{6^2}$个,这里可以看出来符合容斥原理。
 
-($ps$:这条涉及莫比乌斯反演,还没学,学了再看)
+**$Q$:即然这是容斥原理，和莫比乌斯函数有什么关系？**
+答：从现实意义上去看看：
+- $2,3,5$都是一个质数因子，它的系数是$1$
+- $4=2^2$,按莫比乌斯函数的说法，系数为$0$,无贡献
+- $6 = 2 \times 3$,有两个质数因子，系数是$-1$
 
-#### 题单
- **[完全平方数](https://www.luogu.com.cn/problem/P4318)**
+这不就是莫比乌斯函数的定义吗？
 
- 题意就是筛去完全平方数及其的倍数,然后输出第k个的值.
+可知以上式子 $\displaystyle =-\sum_{2 \leq d \leq \sqrt{n}} \mu(d)*⌊\frac{n}{d^2}⌋$
+> **注**：为什么只枚举到$\sqrt{n}$,而不是到$n$呢？这是因为：$d>\sqrt{n}$时，$⌊\frac{n}{d^2}⌋$恒等于$0$，再继续也是无贡献，只需要枚举到$\sqrt{n}$即可。
 
-我们要求这个,就想到把1到ki的所有完全平方数和他的倍数筛去,但是一看数据,1e9,线性筛必定t,那再去想办法进行计算,我们先把2的平方4的倍数计算出来,在1到ki中,有ki/4个4的倍数,我们再计算的16的倍数个数时候,会发现在计算4的倍数个数时候已经把16的倍数个数计算过了,这里就重复了,而假设已经计算了4和9的倍数个数,再去计算36的倍数个数就会发现计算了两次,那么就要减去36的倍数个数,这里就已经想到可以用容斥了.这里我们发现这里需要枚举质数的平方的次数,且奇数偶数符号不相同,就会想到莫比乌斯函数.它计算枚举的边界是i*i<=n;我们再用n减去计算的出来的从2开始的到ki的完全平方数的个数即为所求:
+所以无平方因数的数就是 **求补集**=$\displaystyle n-(-\sum_{2 \leq d \leq \sqrt{n}} \mu(d)*⌊\frac{n}{d^2}⌋)=n+\sum_{2 \leq d \leq \sqrt{n}} \mu(d)*⌊\frac{n}{d^2}⌋$个。
 
-![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312151714471.png)
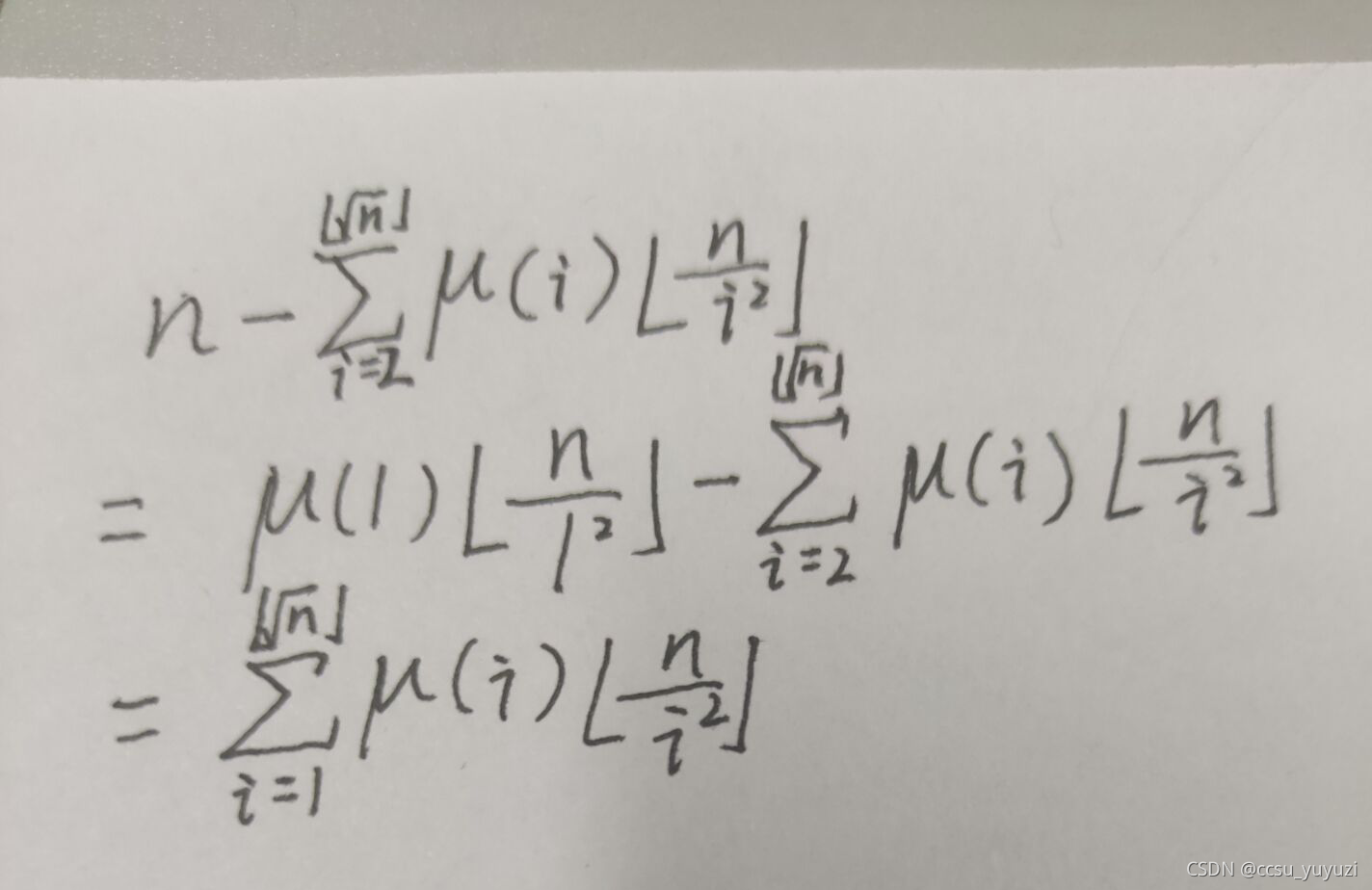
+变形合并,$d=1,\mu(d)=1$(莫比乌斯的分段函数求得)
+$\mu(d)*⌊\frac{n}{d^2}⌋=\mu(1)*(n/1^2)=1*n=n$
 
-当求出来之后,我们就可以用二分来求此时的值:
+此时可以发现这个式子，第一项也可以合并进来，合并成
+$$\displaystyle \sum_{1 \leq d \leq \sqrt{n}} \mu(d)*⌊\frac{n}{d^2}⌋$$
 
+$⌊\frac{n}{d^2}⌋$是整除分块的基本形式，用整除分块优化，区间的数值都是一样的，但每项的符号有加有减，一个个算太慢了，可以给$μ(x)$预处理出前缀和，这样直接用$O(1)$时间计算前缀和，再乘上整除分块的数值就行了~
+
+
+#### $Code$
 ```cpp {.line-numbers}
-#include<iostream>
-#define ll long long 
+#include <bits/stdc++.h>
 using namespace std;
-int vis[40560],mo[40560],p[4253],n;
-void init()
-{
-    int tot=0,k;
-    mo[1]=1;
-    for(int i=2;i<=40559;i++)
-    {
-        if(vis[i]==0)
-        {
-            p[++tot]=i;
-            mo[i]=-1;
+#define int long long
+#define endl "\n"
+const int M = 110;      // 询问次数
+const int N = 10000010; // 莫比乌斯函数值的极限数据上限,sqrt(1e14)=1e7
+int n, sqrtN;           // T次询问，每次都是1~n,sqrtN=sqrt(max(n)),真实上限
+int q[M];               // T次询问，用q数组记录下来
+
+// 筛法求莫比乌斯函数(枚举约数)
+int mu[N], sum[N]; // sum[N]:梅滕斯函数,也就是莫比乌斯函数的前缀和
+int primes[N], cnt;
+bool st[N];
+void get_mobius(int n) {
+    mu[1] = 1;
+    for (int i = 2; i <= n; i++) {
+        if (!st[i]) {
+            primes[cnt++] = i;
+            mu[i] = -1;
         }
-        for(int j=1;j<=tot&&(k=i*p[j])<=40559;j++)
-        {
-            vis[k]=1;
-            if(i%p[j]!=0)mo[k]=-mo[i];
-            else 
-            {
-                mo[k]=0;
+        for (int j = 0; primes[j] <= n / i; j++) {
+            int t = primes[j] * i;
+            st[t] = true;
+            if (i % primes[j] == 0) {
+                mu[t] = 0;
                 break;
             }
+            mu[t] = -mu[i];
         }
     }
+    // 维护u(x)前缀和:梅滕斯函数
+    for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
 }
-bool judge(int x)
-{
-	ll ans=0;int i;
-    for(int i=1;i*i<=x;i++)
-    {
-        ans+=mo[i]*(x/(i*i));
+
+signed main() {
+#ifndef ONLINE_JUDGE
+    freopen("SQP4168.in", "r", stdin);
+#endif
+    int T;
+    cin >> T;
+    for (int i = 1; i <= T; i++) {
+        cin >> q[i];
+        n = max(n, q[i]); // 找到最大的n,这样可以避免重复计算
+    }
+    sqrtN = sqrt(n); // 最大的n，只需要枚举到sqrt(n)即可
+    // 对有效范围内的数字求莫比乌斯函数
+    get_mobius(sqrtN); // 线性求莫比乌斯函数, 前缀和
+
+    for (int i = 1; i <= T; i++) {              // 离线处理，对于每个询问进行回答
+        n = q[i];                               // 第i次的n值
+        int ans = 0;                            // 初始化返回结果
+        for (int l = 1, r; l <= n; l = r + 1) { // 整除分块
+            if (n / (l * l) == 0) break;
+            // n / (l * l): 分块的左边界是l,值是n/(l*l),如果n<(l*l)时，l再长大也没用，也都是0
+            // n/(l*l):整除分块中整个分块内的个数值，从n/(l*l)~n/(r*r)是同一个值
+            r = sqrt(n / (n / (l * l)));                // 求出右边界r
+            ans += n / (l * l) * (sum[r] - sum[l - 1]); // 利用莫比乌斯函数值前缀和求块的贡献
+        }
+        cout << ans << endl;
     }
-    if(ans>=n)return true;
-    else return false;
 }
-int main()
-{
-    int t;
-    ll l,r,mid;
-    init();
-    scanf("%d",&t);
-    while(t--)
-    {
-        scanf("%d",&n);
-        l=n,r=1644934082;
-        while(l<r) 
-        {
-            // cout<<l<<" oo "<<r<<endl;
-			mid=(l+r)>>1;
-			if(judge(mid)) 
-                r=mid;
-			else l=mid+1;
-		}
-        printf("%lld\n",r);
+```
+
+ **[$P4318$ 完全平方数](https://www.luogu.com.cn/problem/P4318)**
+
+**题意**
+小$X$自幼就很喜欢数。但奇怪的是，他十分讨厌完全平方数。他觉得这些数看起来很令人难受。由此，他也讨厌所有是完全平方数的正整数倍的数。然而这丝毫不影响他对其他数的热爱。
+
+这天是小$X$的生日，小$W$想送一个数给他作为生日礼物。当然他不能送一个小$X$讨厌的数。他列出了所有小$X$不讨厌的数，然后选取了第$K$个数送给了小$X$。小$X$很开心地收下了。
+
+然而现在小$W$却记不起送给小$X$的是哪个数了。你能帮他一下吗？
+
+**解法**
+设$f(n)$表示在$1$到$n$中小$X$不讨厌的数的数量。显然$f(n)$是 **单调递增** 的，所以我们可以二分答案。
+> **注**: 与上一题的区别在于上一题明确给出了最大值$n$,也就是右边界的范围，本题没有告诉我们范围，需要我们自己找到右边界。随着右边界越来越大，肯定符合条件的数字个数也会越来越多，也就是上面说到的单调性。我们可以用二分来假设一个右边界，然后不断的收缩区间来找到准备的右边界:在上道题的基础上加上二分，判断$1$到$mid$是否有$K$个无平方因子的数，以此改变左右边界即可。
+
+```cpp {.line-numbers}
+#include <bits/stdc++.h>
+using namespace std;
+#define int long long
+#define endl "\n"
+const int N = 100010;
+
+// 筛法求莫比乌斯函数(枚举约数)
+int mu[N];
+int primes[N], cnt;
+bool st[N];
+void get_mobius(int n) {
+    mu[1] = 1;
+    for (int i = 2; i <= n; i++) {
+        if (!st[i]) {
+            primes[cnt++] = i;
+            mu[i] = -1;
+        }
+        for (int j = 0; primes[j] <= n / i; j++) {
+            int t = primes[j] * i;
+            st[t] = true;
+            if (i % primes[j] == 0) {
+                mu[t] = 0;
+                break;
+            }
+            mu[t] = -mu[i];
+        }
+    }
+}
+int check(int mid, int k) {
+    int res = 0;
+    for (int i = 1; i * i <= mid; i++) // 枚举范围内每个平方数
+        res += mu[i] * (mid / i / i);
+    return res >= k;
+}
+
+signed main() {
+    // 获取莫比乌斯函数值
+    get_mobius(N - 1);
+
+    int T, k;
+    cin >> T; // T组测试数据
+    while (T--) {
+        cin >> k; // 第k个数
+        int l = 1, r = 2e9;
+        while (l < r) {
+            int mid = l + r >> 1;
+            if (check(mid, k))
+                r = mid;
+            else
+                l = mid + 1;
+        }
+        cout << r << endl;
     }
-    return 0;
 }
 ```
 
-例题:数字染色
+#### 例题:数字染色
 题目意思:
 
 给一个数组,在其中选数,看可以最多选出多少个gcd(最大公约数)>1的集合.
@@ -295,6 +349,9 @@ int main()
 }
 ```
 
-ps:最后结果防止取模出负数要加上mod再取模.
 
-之后会继续学习莫比乌斯反演的,如果本蒟蒻有什么错误望大佬指正.
+https://blog.csdn.net/qq_49593247/article/details/120394226
+
+https://www.cnblogs.com/letlifestop/p/10262757.html
+
+// https://blog.csdn.net/qq_42887171/article/details/95237740