|
|
|
|
@ -1,39 +1,13 @@
|
|
|
|
|
## 莫比乌斯函数
|
|
|
|
|
https://blog.csdn.net/qq_49593247/article/details/120394226
|
|
|
|
|
|
|
|
|
|
https://www.cnblogs.com/letlifestop/p/10262757.html
|
|
|
|
|
## 莫比乌斯函数专题
|
|
|
|
|
|
|
|
|
|
// https://blog.csdn.net/qq_42887171/article/details/95237740
|
|
|
|
|
### 一、莫比乌斯函数
|
|
|
|
|
|
|
|
|
|
要学习莫比乌斯函数需要学习 到 **积性函数**,深度理解 **欧拉筛** 。
|
|
|
|
|
先明确一点,莫比乌斯函数并不是什么很高大上的东西,它其实只是一个由容斥系数所构成的函数。
|
|
|
|
|
|
|
|
|
|
### 一、积性函数
|
|
|
|
|
**[视频讲解:两分钟学会墨比乌斯函数](https://www.bilibili.com/video/BV12P4y1Q7tc/)**
|
|
|
|
|
|
|
|
|
|
#### 1. 定义
|
|
|
|
|
|
|
|
|
|
**积性函数**:若$gcd(a,b)=1$,且满足$f(a*b)=f(a)*f(b)$,则称$f(x)$为 **积性函数**
|
|
|
|
|
|
|
|
|
|
**完全积性函数**:对于任意正整数$a,b$,都满足$f(a*b)=f(a)*f(b)$,则称$f(x)$为 **完全积性函数**
|
|
|
|
|
|
|
|
|
|
#### 2. 性质
|
|
|
|
|
|
|
|
|
|
1. 若$f(n),g(n)$均为积性函数,则函数$h(n)=f(n)*g(n)$也是积性函数
|
|
|
|
|
|
|
|
|
|
2. 若$f(n)$为积性函数,则函数$c*f(n)$($c$是常数)也是积性函数,反之一样
|
|
|
|
|
|
|
|
|
|
3. **任何积性函数都能应用线性筛**,在$O(n)$时间内求出$1\sim n$项(**莫比乌斯函数要用到**),像素数,欧拉函数等都是 **积性函数**。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
### 二、莫比乌斯函数
|
|
|
|
|
|
|
|
|
|
#### 1. 用途
|
|
|
|
|
|
|
|
|
|
我们举例一道经典的应用题,求$1$到$N$中与$a$互质的数的个数:根据容斥原理,设$S_i$为$1$到$N$中和$a$有公因子$i$的数的个数,答案为$N−S_2-S_3-S_5-S_7...+S_{2,3}+S_{3,5}+S_{2,5}...$,可以发现,其答案为$\large \displaystyle \sum_{i=1}^{N}\mu(i)*S_i$。
|
|
|
|
|
|
|
|
|
|
> **注**:在使用容斥原理解决计数问题时,莫比乌斯函数的值就是每一项的系数,要么是$1$,要么是$-1$。这是因为莫比乌斯函数在容斥原理中的作用就是用来表示每个子集合的权重,从而在计算中起到排除重复计数的作用。
|
|
|
|
|
|
|
|
|
|
#### 2. 定义
|
|
|
|
|
|
|
|
|
|
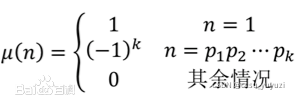
|
|
|
|
|
|
|
|
|
|
莫比乌斯函数是个分段函数,它的意思:
|
|
|
|
|
@ -50,103 +24,71 @@ https://www.cnblogs.com/letlifestop/p/10262757.html
|
|
|
|
|
函数值 1 -1 -1 0 -1 1 -1 0 0 1 -1 0 -1 1 1 0 -1 0 -1 0
|
|
|
|
|
数 字: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
#### 2. 用途
|
|
|
|
|
|
|
|
|
|
我们举例一道经典的应用题,求$1$到$N$中与$a$互质的数的个数:根据容斥原理,设$S_i$为$1$到$N$中和$a$有公因子$i$的数的个数,答案为$N−S_2-S_3-S_5-S_7...+S_{2,3}+S_{3,5}+S_{2,5}...$,可以发现,其答案为$\large \displaystyle \sum_{i=1}^{N}\mu(i)*S_i$。
|
|
|
|
|
|
|
|
|
|
> **注**:在使用容斥原理解决计数问题时,莫比乌斯函数的值就是每一项的系数,要么是$1$,要么是$-1$。这是因为莫比乌斯函数在容斥原理中的作用就是用来表示每个子集合的权重,从而在计算中起到排除重复计数的作用。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 3. 求单个数字的莫比乌斯函数值
|
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
//单个数的莫比乌斯函数
|
|
|
|
|
int getmob(LL x) {
|
|
|
|
|
// 单个数的莫比乌斯函数
|
|
|
|
|
int getmob(int x) {
|
|
|
|
|
int sum = 0;
|
|
|
|
|
for (LL i = 2; i <= x / i; i++) { //从2开始,一直到 sqrt(x),枚举所有可能存的小因子
|
|
|
|
|
for (int i = 2; i <= x / i; i++) { // 从2开始,一直到 sqrt(x),枚举所有可能存的小因子
|
|
|
|
|
int cnt = 0;
|
|
|
|
|
if (x % i == 0) { //如果x可以整除i
|
|
|
|
|
while (x % i == 0) cnt++, x /= i; //计数,并且不断除掉这个i因子
|
|
|
|
|
if (cnt > 1) return 0; //如果某个因子,存在两个及以上个,则返回0
|
|
|
|
|
sum++; //记录因子个数
|
|
|
|
|
if (x % i == 0) { // 如果x可以整除i
|
|
|
|
|
while (x % i == 0) cnt++, x /= i; // 计数,并且不断除掉这个i因子
|
|
|
|
|
if (cnt > 1) return 0; // 如果某个因子,存在两个及以上个,则返回0
|
|
|
|
|
sum++; // 记录因子个数
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
if (x != 1) sum++; //如果还存在另一个大因子,那么因子个数+1
|
|
|
|
|
return (sum & 1) ? -1 : 1; //奇数个因子,返回-1,否则返回1
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
#### 4.枚举倍数求莫比乌斯函数(埃氏筛)
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
//枚举倍数求莫比乌斯函数
|
|
|
|
|
LL mu[N] , sum[N];
|
|
|
|
|
void mobius(LL x) {
|
|
|
|
|
mu[1] = 1;
|
|
|
|
|
for (LL i = 1; i <= x; i++)
|
|
|
|
|
for (LL j = i + i; j <= x; j += i)
|
|
|
|
|
mu[j] -= mu[i];
|
|
|
|
|
// 维护u(x)前缀和
|
|
|
|
|
for (LL i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
|
|
|
|
|
if (x != 1) sum++; // 如果还存在另一个大因子,那么因子个数+1
|
|
|
|
|
return (sum & 1) ? -1 : 1; // 奇数个因子,返回-1,否则返回1
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 5.枚举约数求莫比乌斯函数(欧拉筛)
|
|
|
|
|
#### 4.欧拉筛扩展求莫比乌斯函数
|
|
|
|
|
**[视频讲解](https://www.bilibili.com/video/BV1Te4y1C7DP)**
|
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
LL mu[N] , sum[N];
|
|
|
|
|
// 筛法求莫比乌斯函数(枚举约数)
|
|
|
|
|
int mu[N], sum[N]; // sum[N]:梅滕斯函数,也就是莫比乌斯函数的前缀和
|
|
|
|
|
int primes[N], cnt;
|
|
|
|
|
bool st[N];
|
|
|
|
|
void get_mobius2(LL n) {
|
|
|
|
|
void get_mobius(int n) {
|
|
|
|
|
mu[1] = 1;
|
|
|
|
|
for (LL i = 2; i <= n; i++) {
|
|
|
|
|
for (int i = 2; i <= n; i++) {
|
|
|
|
|
if (!st[i]) {
|
|
|
|
|
primes[cnt++] = i;
|
|
|
|
|
mu[i] = -1;
|
|
|
|
|
}
|
|
|
|
|
for (LL j = 0; primes[j] <= n / i; j++) {
|
|
|
|
|
LL t = primes[j] * i;
|
|
|
|
|
for (int j = 0; primes[j] <= n / i; j++) {
|
|
|
|
|
int t = primes[j] * i;
|
|
|
|
|
st[t] = true;
|
|
|
|
|
if (i % primes[j] == 0) {
|
|
|
|
|
mu[t] = 0;
|
|
|
|
|
break;
|
|
|
|
|
}
|
|
|
|
|
mu[t] = mu[i] * -1;
|
|
|
|
|
mu[t] = -mu[i];
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
// 维护u(x)前缀和
|
|
|
|
|
for (LL i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
|
|
|
|
|
// 维护u(x)前缀和:梅滕斯函数
|
|
|
|
|
for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
#### 6、性质$I$
|
|
|
|
|
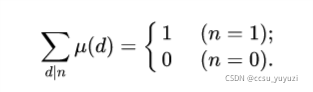
|
|
|
|
|
|
|
|
|
|
该图意为$n$的所有因子的莫比乌斯值的和只有在$n=1$时成立为$1$,其余通通为$0$;
|
|
|
|
|
|
|
|
|
|
对这个性质的证明:
|
|
|
|
|
|
|
|
|
|
首先我们可以把$n$分解为很多个质数相乘(此时质数的幂不一定为$1$):
|
|
|
|
|
令 $\large n=p_1^ {a_1}* p_2^ {a_2}* ... *p_k^{a_k}$
|
|
|
|
|
|
|
|
|
|
$\displaystyle \sum_{d | n} \mu(d)$ 这是求$n$的所有约数的莫比乌斯函数值的和,相当于在$p_1,p_2,p_3,...$这些素数中选择若干个质因子相乘来组成所有约数。
|
|
|
|
|
|
|
|
|
|
根据莫比乌斯函数性质,包含有素数平方的约数不用计算,他对答案的贡献值为$0$,所以我们可以把$n$分解的质数的次数全部消除为$1$,只有当莫比乌斯值为$-1$或者$1$时才对结果有贡献.那么问题就单纯的变为在$k$个$n$的质因子中选$0$到$k$个值组成约数,再将这些约数的值相加:
|
|
|
|
|
|
|
|
|
|
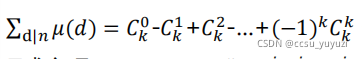
|
|
|
|
|
### 二、题单
|
|
|
|
|
**[$P4318$ 完全平方数](https://www.luogu.com.cn/problem/P4318)**
|
|
|
|
|
|
|
|
|
|
注意,这里的符号并不是全为加法,而是隔一个加隔一个减,这是因为莫比乌斯函数是积性函数,当选的数是奇数个时为值为负,反之为正,又因二项式定理,将$-1$和$1$带入,可以得到结果为$0$.
|
|
|
|
|
**题意**
|
|
|
|
|
筛去完全平方数及其的倍数,然后输出第$k$个的值。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 7、性质$II$
|
|
|
|
|
对任意正整数n
|
|
|
|
|
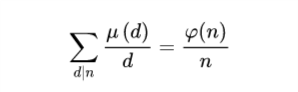
|
|
|
|
|
|
|
|
|
|
(ps:这条涉及莫比乌斯反演,还没学,学了再看)
|
|
|
|
|
|
|
|
|
|
好了,这就是大致知识,我学完了这个还是不知道这东西到底有什么用,还是得靠实战:
|
|
|
|
|
|
|
|
|
|
#### 题单
|
|
|
|
|
**[完全平方数](https://www.luogu.com.cn/problem/P4318)**
|
|
|
|
|
|
|
|
|
|
题意就是筛去完全平方数及其的倍数,然后输出第k个的值.
|
|
|
|
|
|
|
|
|
|
我们要求这个,就想到把1到ki的所有完全平方数和他的倍数筛去,但是一看数据,1e9,线性筛必定t,那再去想办法进行计算,我们先把2的平方4的倍数计算出来,在1到ki中,有ki/4个4的倍数,我们再计算的16的倍数个数时候,会发现在计算4的倍数个数时候已经把16的倍数个数计算过了,这里就重复了,而假设已经计算了4和9的倍数个数,再去计算36的倍数个数就会发现计算了两次,那么就要减去36的倍数个数,这里就已经想到可以用容斥了.这里我们发现这里需要枚举质数的平方的次数,且奇数偶数符号不相同,就会想到莫比乌斯函数.它计算枚举的边界是i*i<=n;我们再用n减去计算的出来的从2开始的到ki的完全平方数的个数即为所求:
|
|
|
|
|
我们要求这个,就想到把$1$到$k_i$的所有完全平方数和他的倍数筛去,但是一看数据,$1e9$,线性筛必定$T$,那再去想办法进行计算,我们先把$2$的平方$4$的倍数计算出来,在$1$到$k_i$中,有$k_i/4$个$4$的倍数,我们再计算的$16$的倍数个数时候,会发现在计算$4$的倍数个数时候已经把$16$的倍数个数计算过了,这里就重复了,而假设已经计算了$4$和$9$的倍数个数,再去计算$36$的倍数个数就会发现计算了两次,那么就要减去$36$的倍数个数,这里就已经想到可以用 **容斥** 了.这里我们发现这里 **需要枚举质数的平方的次数** ,且奇数偶数符号不相同,就会想到 **莫比乌斯函数**.它计算枚举的边界是$i*i<=n$;我们再用$n$减去计算的出来的从$2$开始的到$k_i$的完全平方数的个数即为所求:
|
|
|
|
|
|
|
|
|
|
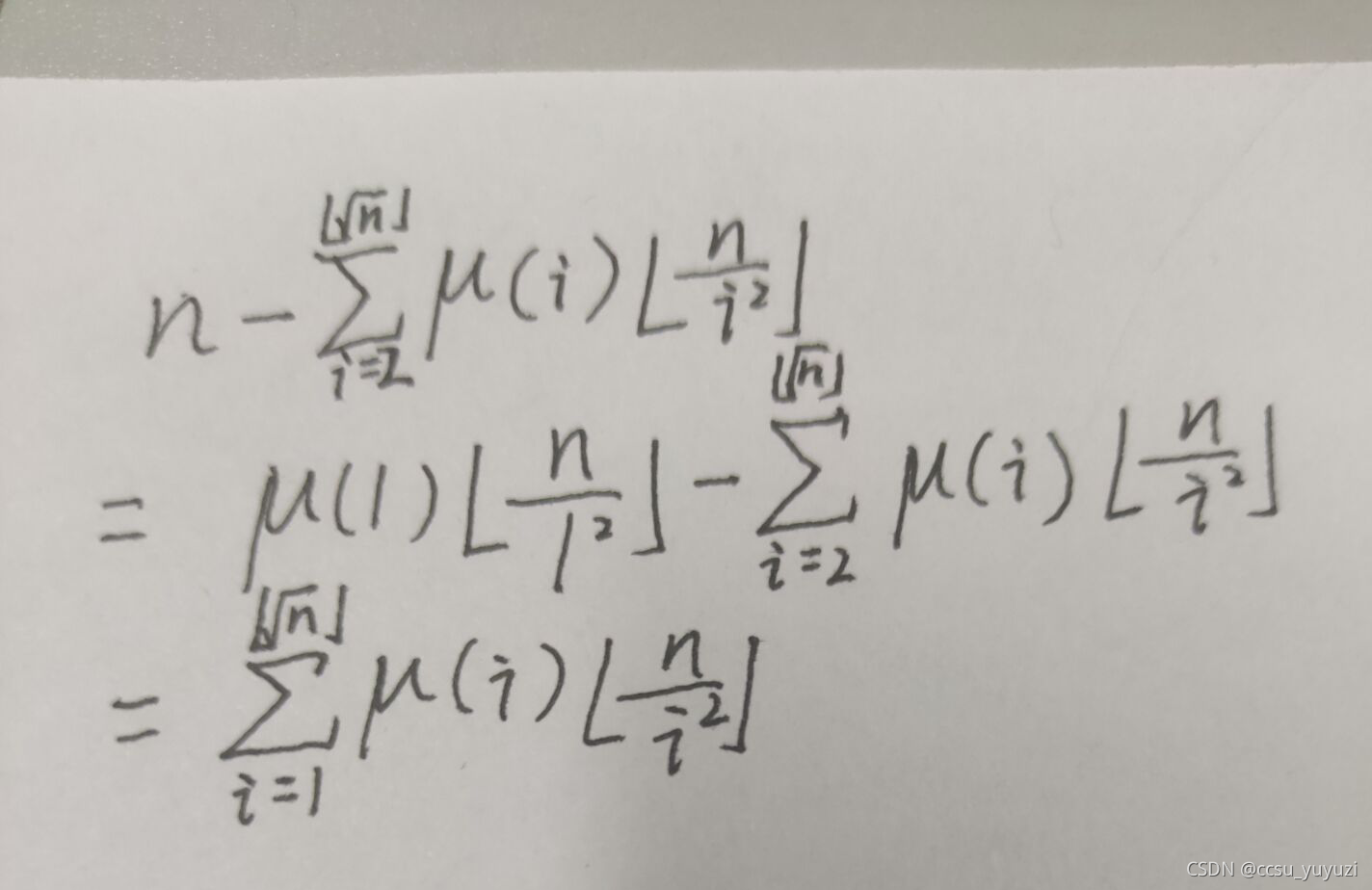
|
|
|
|
|
|
|
|
|
|
@ -214,7 +156,7 @@ int main()
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
例题:数字染色
|
|
|
|
|
#### 例题:数字染色
|
|
|
|
|
题目意思:
|
|
|
|
|
|
|
|
|
|
给一个数组,在其中选数,看可以最多选出多少个gcd(最大公约数)>1的集合.
|
|
|
|
|
@ -292,6 +234,9 @@ int main()
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
ps:最后结果防止取模出负数要加上mod再取模.
|
|
|
|
|
|
|
|
|
|
之后会继续学习莫比乌斯反演的,如果本蒟蒻有什么错误望大佬指正.
|
|
|
|
|
https://blog.csdn.net/qq_49593247/article/details/120394226
|
|
|
|
|
|
|
|
|
|
https://www.cnblogs.com/letlifestop/p/10262757.html
|
|
|
|
|
|
|
|
|
|
// https://blog.csdn.net/qq_42887171/article/details/95237740
|
|
|
|
|
|