diff --git a/TangDou/AcWing_TiGao/T1/LIS/1012.md b/TangDou/AcWing_TiGao/T1/LIS/1012.md
index 9baf869..a38601c 100644
--- a/TangDou/AcWing_TiGao/T1/LIS/1012.md
+++ b/TangDou/AcWing_TiGao/T1/LIS/1012.md
@@ -54,7 +54,7 @@ $1≤N≤5000,0≤x_i≤10000$
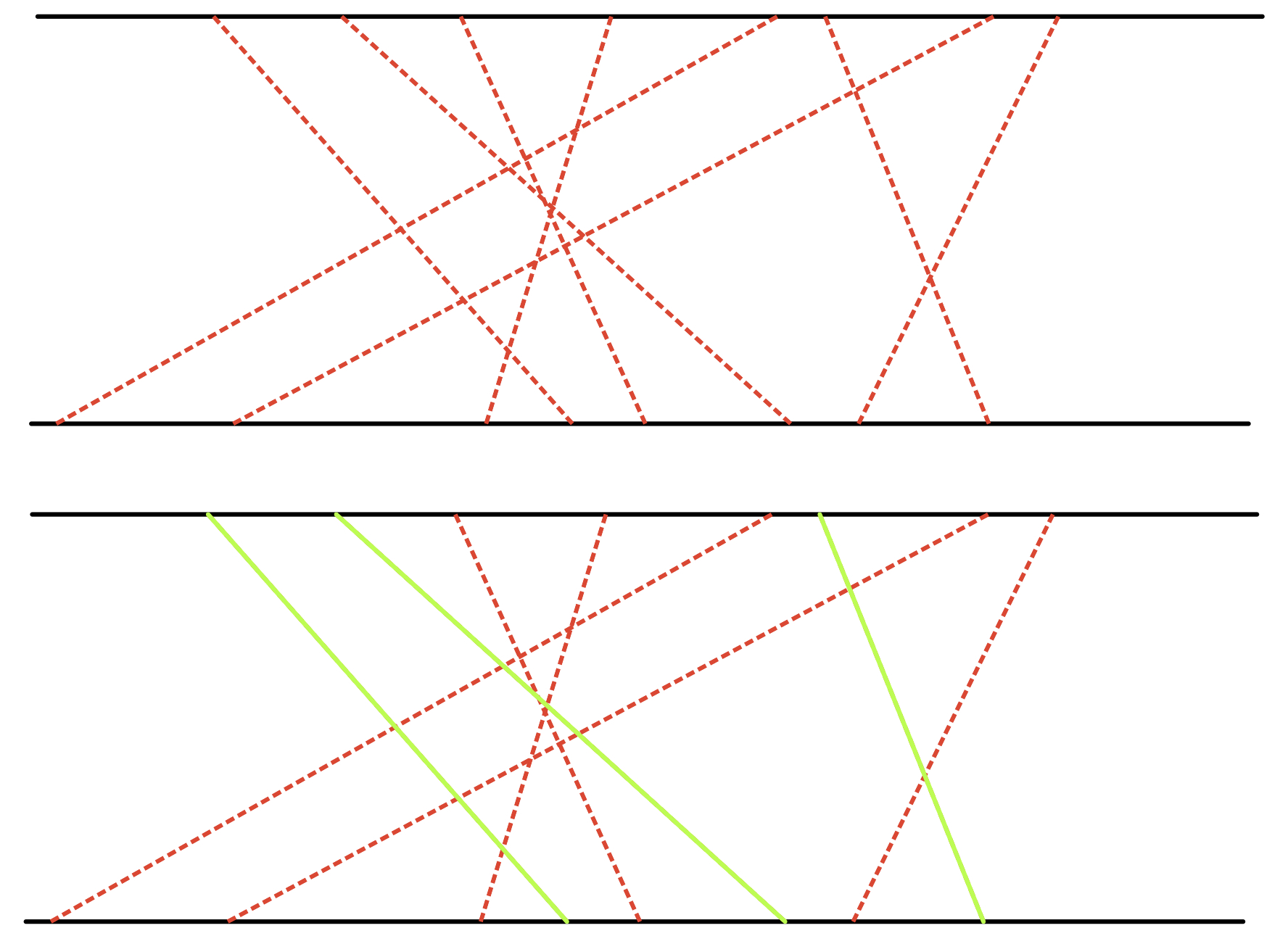 #### 1、什么情况会交叉?
-什么情况会造成桥出现交叉呢?手动模拟可知:当两座桥对应的两对城市($(x_1,y_1),(x_2,y_2)$)出现了下面的情况:
+手动模拟可知:当两座桥对应的两对城市($(x_1,y_1),(x_2,y_2)$)出现了下面的情况:
$$
\large \left\{\begin{matrix}
@@ -72,14 +72,14 @@ $$
#### 2、暴力怎么做?
* 如果按照暴力的思路去思考的话,因为每座桥都可以选择建或者不建两种情况,所以要枚举所有的可能性,需要枚举的次数为$2^N$,其中$N≤5000$,肯定会$TLE$啊,需要优化。
-* 如果暴力,需要枚举每一个城市,那么枚举序是什么呢?城市编号吗?**~~开什么玩笑,题目根本也没有给你城市编号,你也不知道城市编号啊,而且这玩意也没用啊,你创造一个新概念出来给自己找罪受吗?~~~**,那题目中给了啥东西?**友好城市的坐标**!,那你要枚举坐标,**是不是得排个序,从小到大讨论**?
+* 如果暴力,需要枚举每一个**友好城市的坐标**!,既然要枚举坐标,**是不是得排个序,从小到大讨论**,要不逆序不逆序怎么判断?
当你想到需要把一端坐标从小到大排序时,就马上会想到,那另一端怎么办?对应关系不能丢失啊,所以,需要使用`pair`进行处理。
到这,似乎快看到曙光: 一端顺序由小到大,讨论另一端,怎么样才能让在没有交叉的情况下桥的数量还最多呢?当然是升序的序列越长越好,转化为求$LIS$问题了!
#### 3、总结
-* 多个数对的问题,套路是:对数对的第一维的自变量进行排序,然后再处理第二维的因变量,这样操作,可以起到类似于 降维 的作用,使问题简化。
+* 多个数对的问题,套路:对数对的第一维排序,再处理第二维。这样操作,可以起到类似于 降维 的作用,使问题简化。
* 本题还是有一些思维的难度,需要对问题进行转化。用 **数对** 描述问题比较好想,为什么要按左端点进行排序呢?似乎对于数对而言,大多数情况需要固定一个端点,比如[区间合并](https://www.cnblogs.com/littlehb/p/15242447.html),如果我们能想到这是一个用数对描述的问题,不妨先想一下是不是在按左端点排序一下。
@@ -148,4 +148,10 @@ int main() {
printf("%d\n", fl);
return 0;
}
-```
\ No newline at end of file
+```
+
+### 五、关键字
+- 转化模型
+- 数对
+- 排序 (第一维)
+- $LIS$ (第二维)
\ No newline at end of file
#### 1、什么情况会交叉?
-什么情况会造成桥出现交叉呢?手动模拟可知:当两座桥对应的两对城市($(x_1,y_1),(x_2,y_2)$)出现了下面的情况:
+手动模拟可知:当两座桥对应的两对城市($(x_1,y_1),(x_2,y_2)$)出现了下面的情况:
$$
\large \left\{\begin{matrix}
@@ -72,14 +72,14 @@ $$
#### 2、暴力怎么做?
* 如果按照暴力的思路去思考的话,因为每座桥都可以选择建或者不建两种情况,所以要枚举所有的可能性,需要枚举的次数为$2^N$,其中$N≤5000$,肯定会$TLE$啊,需要优化。
-* 如果暴力,需要枚举每一个城市,那么枚举序是什么呢?城市编号吗?**~~开什么玩笑,题目根本也没有给你城市编号,你也不知道城市编号啊,而且这玩意也没用啊,你创造一个新概念出来给自己找罪受吗?~~~**,那题目中给了啥东西?**友好城市的坐标**!,那你要枚举坐标,**是不是得排个序,从小到大讨论**?
+* 如果暴力,需要枚举每一个**友好城市的坐标**!,既然要枚举坐标,**是不是得排个序,从小到大讨论**,要不逆序不逆序怎么判断?
当你想到需要把一端坐标从小到大排序时,就马上会想到,那另一端怎么办?对应关系不能丢失啊,所以,需要使用`pair`进行处理。
到这,似乎快看到曙光: 一端顺序由小到大,讨论另一端,怎么样才能让在没有交叉的情况下桥的数量还最多呢?当然是升序的序列越长越好,转化为求$LIS$问题了!
#### 3、总结
-* 多个数对的问题,套路是:对数对的第一维的自变量进行排序,然后再处理第二维的因变量,这样操作,可以起到类似于 降维 的作用,使问题简化。
+* 多个数对的问题,套路:对数对的第一维排序,再处理第二维。这样操作,可以起到类似于 降维 的作用,使问题简化。
* 本题还是有一些思维的难度,需要对问题进行转化。用 **数对** 描述问题比较好想,为什么要按左端点进行排序呢?似乎对于数对而言,大多数情况需要固定一个端点,比如[区间合并](https://www.cnblogs.com/littlehb/p/15242447.html),如果我们能想到这是一个用数对描述的问题,不妨先想一下是不是在按左端点排序一下。
@@ -148,4 +148,10 @@ int main() {
printf("%d\n", fl);
return 0;
}
-```
\ No newline at end of file
+```
+
+### 五、关键字
+- 转化模型
+- 数对
+- 排序 (第一维)
+- $LIS$ (第二维)
\ No newline at end of file

