'commit'

TangDou/Topic/【换根】dfs专题.md

@@ -825,32 +825,13 @@ int main() {
 
 #### [$POJ3585$ $Accumulation$ $Degree$](http://poj.org/problem?id=3585)
 
-**题意**
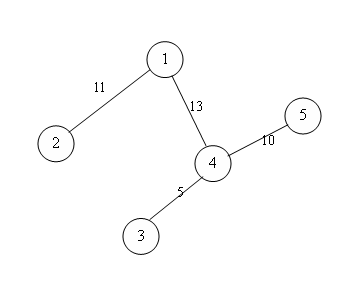
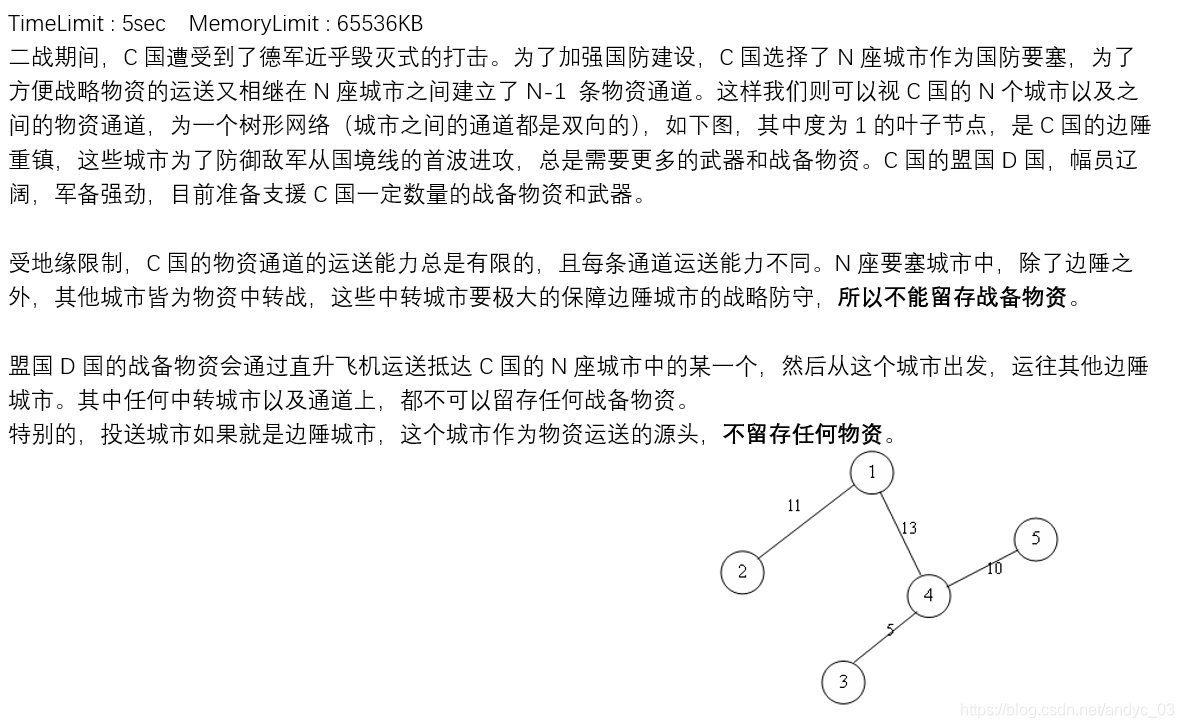
-一个树形水系，有$n$个结点，根结点称为 **源点**，叶子结点称为 **汇点**，每条边都有水量限制$C_{x,y}$($x,y$为这条边的两个端点)，源点单位时间流出的水量称为整个水系的流量，求以哪一个结点作为源点整个水系的流量最大。
-
-![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401161121787.png)
-
-```cpp {.line-numbers}
-A(1)=11+5+8=24
-Details:	1->2	11
-　	1->4->3	5
-　	1->4->5	8(since 1->4 has capacity of 13)
 
-A(2)=5+6=11
-Details:	2->1->4->3	5
-　	2->1->4->5	6
+**题意**
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401161333814.png)
 
-A(3)=5
-Details:	3->4->5	5
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401161333206.png)
 
-A(4)=11+5+10=26
-Details:	4->1->2	11
-　	4->3	5
-　	4->5	10
 
-A(5)=10
-Details:	5->4->1->2	10
-```
 **思路分析**
 
 这是一道 **不定根** 的树形$DP$问题，这类题目的特点是，给定一个树形结构，需要以每个结点为根进行一系列统计。我们一般通过两次扫描来求解此类问题：
@@ -858,10 +839,16 @@ Details:	5->4->1->2	10
 - 1.第一次扫描，任选一个点为根，在 **有根树** 上执行一次树形$DP$。
 - 2.第二次扫描，从刚才选出的根出发，对整棵树执行一次$DFS$，在每次递归前进行 **自上而下** 的推导，计算出 **换根** 之后的解。
 
-首先，我们选择结点$1$，然后树形$DP$一下:
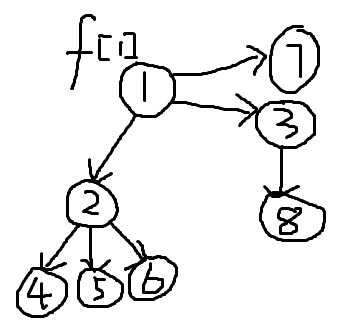
-1、求出$f$数组($f[i]$表示以$1$这根的树，以$i$为根的子树中流量的最大值)。
-2、设$g[u]$表示以$u$为源点，流向整个水系的最大流量，则显然$g[1]=f[1]$。假设$g[u]$已经求出，考虑其子结点$v$，则$f[v]$包含两部分：
+**本题思路**
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401161324729.png)
+
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401161325661.png)
+
+首先，选择$1$号结点，然后树形$dfs$:
+- 1、求出$f$数组($f[i]$表示以$1$这根的树，以$i$为根的子树中流量的最大值)。
+- 2、设$g[u]$表示以$u$为源点，流向整个水系的最大流量，则显然$g[1]=f[1]$。
 
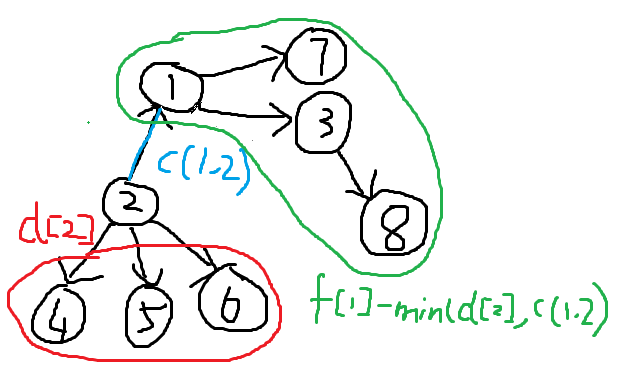
+假设$g[u]$已经求出，考虑其子结点$v$，则$g[v]$包含两部分：
 - 1.从$v$流向以$v$为根的子树的流量，已经计算出来。
 - 2.从$v$沿着到父节点$u$的河道，进而流向水系中其他部分的流量。