diff --git a/TangDou/AcWing/MinimalSpanningTree/858.md b/TangDou/AcWing/MinimalSpanningTree/858.md
index 7c3ef57..a8e727d 100644
--- a/TangDou/AcWing/MinimalSpanningTree/858.md
+++ b/TangDou/AcWing/MinimalSpanningTree/858.md
@@ -64,10 +64,10 @@ $1≤n≤500,1≤m≤10^5$,
$prim$ 算法采用的是一种 **贪心** 的策略,每次将离连通部分的最近的点和点对应的边加入的连通部分,连通部分逐渐扩大,最后将整个图连通起来,并且边长之和最小。
#### 算法步骤
-1. 把所有距离`dist[N]`初始化为$INF$。
-2. 用一个 `pre` 数组保存节点的是和谁连通的。`pre[i] = k` 表示节点 `i` 和节点 `k` 之间需要有一条边。初始时,`pre` 的各个元素置为 `-1`。
+1. 把所有距离`dis[N]`初始化为$INF$。
+2. 用一个 `pre` 数组保存节点的前驱节点是谁。`pre[i] = k` 表示节点 `i` 和节点 `k` 之间需要有一条边。初始时,`pre` 的各个元素置为 `-1`。
3. 循环$n$次,将所有点准备加入到集合中。
- - 找出不在集合中的(`!st[j]`)距离集合最近的点`dist[j]`,如果是有多个距离一样近,那么选择号小的那个,命名为`t`。
+ - 找出不在集合中的(`!st[j]`)距离集合最近的点`dis[j]`,如果是有多个距离一样近,那么选择号小的那个,命名为`t`。
- 累加最小权值
- 利用$t$更新未加入集合中的其它各点到集合的最短距离
- 将$t$加入到集合中
@@ -78,39 +78,39 @@ $prim$ 算法采用的是一种 **贪心** 的策略,每次将离连通部分的
1. 要将所有景点连通起来,并且边长之和最小,步骤如下:
用一个 $st$ 数组表示节点是否已经连通。$st[i]$ 为真,表示已经连通,$st[i]$ 为假,表示还没有连通。初始时,$st$ 各个元素为假。即所有点还没有连通。
-用一个 $dist$ 数组保存各个点到连通部分的最短距离,$dist[i]$ 表示 $i$ 节点到连通部分的最短距离。初始时,$dist$ 数组的各个元素为无穷大。
+用一个 $dis$ 数组保存各个点到连通部分的最短距离,$dis[i]$ 表示 $i$ 节点到连通部分的最短距离。初始时,$dis$ 数组的各个元素为无穷大。
用一个 $pre$ 数组保存节点的是和谁连通的。$pre[i] = k$ 表示节点 $i$ 和节点 $k$ 之间需要有一条边。初始时,$pre$ 的各个元素置为 $-1$。
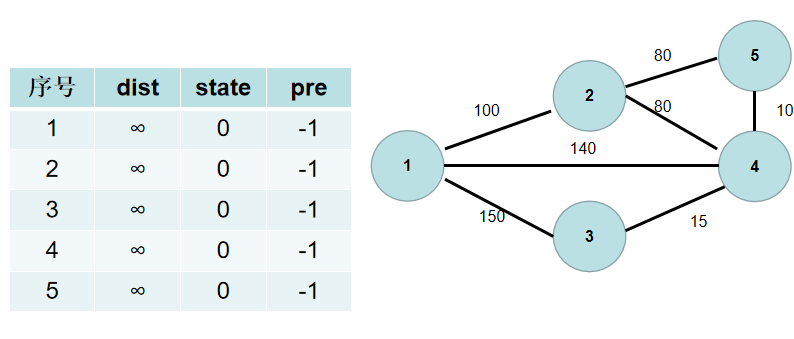 -2. 从 $1$ 号节点开始扩充连通的部分,[之所以从一号结点开始,是因为大家都是距离集合正无穷,那么号小的优先!],所以 $1$ 号节点与连通部分的最短距离为 $0$,即$dist[i]$ 值为 0。
+2. 从 $1$ 号节点开始扩充连通的部分,【之所以从一号结点开始,是因为大家都是距离集合正无穷,那么号小的优先!】,所以 $1$ 号节点与连通部分的最短距离为 $0$,即$dis[i]$ 值为 0。
-2. 从 $1$ 号节点开始扩充连通的部分,[之所以从一号结点开始,是因为大家都是距离集合正无穷,那么号小的优先!],所以 $1$ 号节点与连通部分的最短距离为 $0$,即$dist[i]$ 值为 0。
+2. 从 $1$ 号节点开始扩充连通的部分,【之所以从一号结点开始,是因为大家都是距离集合正无穷,那么号小的优先!】,所以 $1$ 号节点与连通部分的最短距离为 $0$,即$dis[i]$ 值为 0。
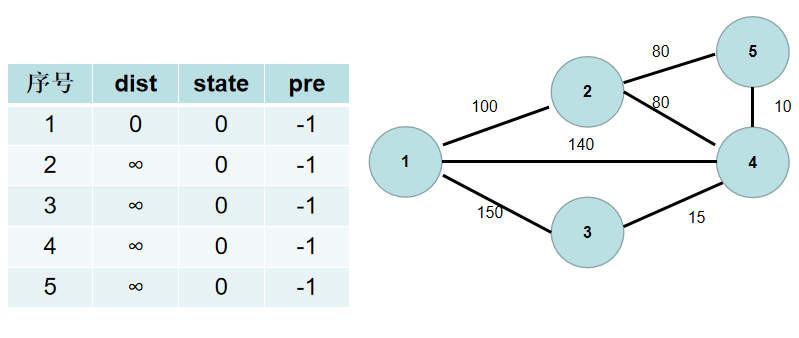 -3. 遍历 $dist$ 数组,找到一个还没有连通起来,但是距离连通部分最近的点,假设该节点的编号是 $t$。$t$节点就是下一个应该加入连通部分的节点,$st[t]$ 置为 $true$。
-用青色点表示还没有连通起来的点,红色点表示连通起来的点。这里青色点中距离最小的是 $dist[1]$,因此 $st[1]$ 置为 $true$。
+3. 遍历 $dis$ 数组,找到一个还没有连通起来,但是距离连通部分最近的点,假设该节点的编号是 $t$。$t$节点就是下一个应该加入连通部分的节点,$st[t]$ 置为 $true$。
+用青色点表示还没有连通起来的点,红色点表示连通起来的点。这里青色点中距离最小的是 $dis[1]$,因此 $st[1]$ 置为 $true$。
-3. 遍历 $dist$ 数组,找到一个还没有连通起来,但是距离连通部分最近的点,假设该节点的编号是 $t$。$t$节点就是下一个应该加入连通部分的节点,$st[t]$ 置为 $true$。
-用青色点表示还没有连通起来的点,红色点表示连通起来的点。这里青色点中距离最小的是 $dist[1]$,因此 $st[1]$ 置为 $true$。
+3. 遍历 $dis$ 数组,找到一个还没有连通起来,但是距离连通部分最近的点,假设该节点的编号是 $t$。$t$节点就是下一个应该加入连通部分的节点,$st[t]$ 置为 $true$。
+用青色点表示还没有连通起来的点,红色点表示连通起来的点。这里青色点中距离最小的是 $dis[1]$,因此 $st[1]$ 置为 $true$。
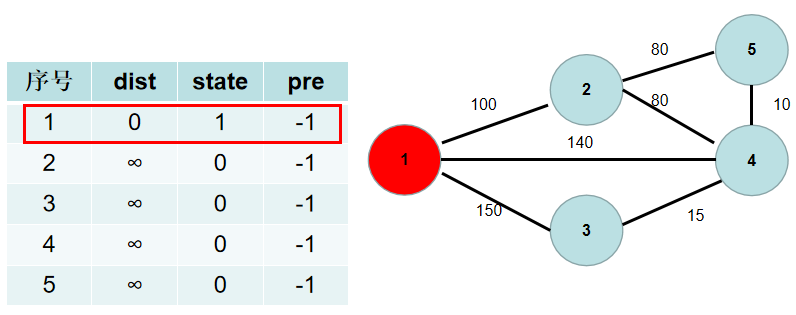 -4.遍历所有与 $t$ 相连但没有加入到连通部分的点 $j$,如果 $j$ 距离连通部分的距离大于 $t \sim j$ 之间的距离,即 $dist[j] > g[t][j]$($g[t][j]$ 为 $t \sim j$ 节点之间的距离),则更新 $dist[j]$ 为 $g[t][j]$。这时候表示,$j$ 到连通部分的最短方式是和 $t$ 相连,因此,更新$pre[j] = t$。
+4.遍历所有与 $t$ 相连但没有加入到连通部分的点 $j$,如果 $j$ 距离连通部分的距离大于 $t \sim j$ 之间的距离,即 $dis[j] > g[t][j]$($g[t][j]$ 为 $t \sim j$ 节点之间的距离),则更新 $dis[j]$ 为 $g[t][j]$。这时候表示,$j$ 到连通部分的最短方式是和 $t$ 相连,因此,更新$pre[j] = t$。
-与节点 $1$ 相连的有 $2$, $3$, $4$ 号节点。$1->2$ 的距离为 $100$,小于 $dist[2]$,$dist[2]$ 更新为 $100$,$pre[2]$ 更新为$1$。$1->4$ 的距离为 $140$,小于 $dist[4]$,$dist[4] $更新为 $140$,$pre[4]$ 更新为$1$。$1->3$ 的距离为 $150$,小于 $dist[3]$,$dist[3]$ 更新为 $150$,$pre[3]$ 更新为$1$。
+与节点 $1$ 相连的有 $2$, $3$, $4$ 号节点。$1 \rightarrow 2$ 的距离为 $100$,小于 $dis[2]$,$dis[2]$ 更新为 $100$,$pre[2]$ 更新为$1$。$1 \rightarrow 4$ 的距离为 $140$,小于 $dis[4]$,$dis[4] $更新为 $140$,$pre[4]$ 更新为$1$。$1 \rightarrow 3$ 的距离为 $150$,小于 $dis[3]$,$dis[3]$ 更新为 $150$,$pre[3]$ 更新为$1$。
-4.遍历所有与 $t$ 相连但没有加入到连通部分的点 $j$,如果 $j$ 距离连通部分的距离大于 $t \sim j$ 之间的距离,即 $dist[j] > g[t][j]$($g[t][j]$ 为 $t \sim j$ 节点之间的距离),则更新 $dist[j]$ 为 $g[t][j]$。这时候表示,$j$ 到连通部分的最短方式是和 $t$ 相连,因此,更新$pre[j] = t$。
+4.遍历所有与 $t$ 相连但没有加入到连通部分的点 $j$,如果 $j$ 距离连通部分的距离大于 $t \sim j$ 之间的距离,即 $dis[j] > g[t][j]$($g[t][j]$ 为 $t \sim j$ 节点之间的距离),则更新 $dis[j]$ 为 $g[t][j]$。这时候表示,$j$ 到连通部分的最短方式是和 $t$ 相连,因此,更新$pre[j] = t$。
-与节点 $1$ 相连的有 $2$, $3$, $4$ 号节点。$1->2$ 的距离为 $100$,小于 $dist[2]$,$dist[2]$ 更新为 $100$,$pre[2]$ 更新为$1$。$1->4$ 的距离为 $140$,小于 $dist[4]$,$dist[4] $更新为 $140$,$pre[4]$ 更新为$1$。$1->3$ 的距离为 $150$,小于 $dist[3]$,$dist[3]$ 更新为 $150$,$pre[3]$ 更新为$1$。
+与节点 $1$ 相连的有 $2$, $3$, $4$ 号节点。$1 \rightarrow 2$ 的距离为 $100$,小于 $dis[2]$,$dis[2]$ 更新为 $100$,$pre[2]$ 更新为$1$。$1 \rightarrow 4$ 的距离为 $140$,小于 $dis[4]$,$dis[4] $更新为 $140$,$pre[4]$ 更新为$1$。$1 \rightarrow 3$ 的距离为 $150$,小于 $dis[3]$,$dis[3]$ 更新为 $150$,$pre[3]$ 更新为$1$。
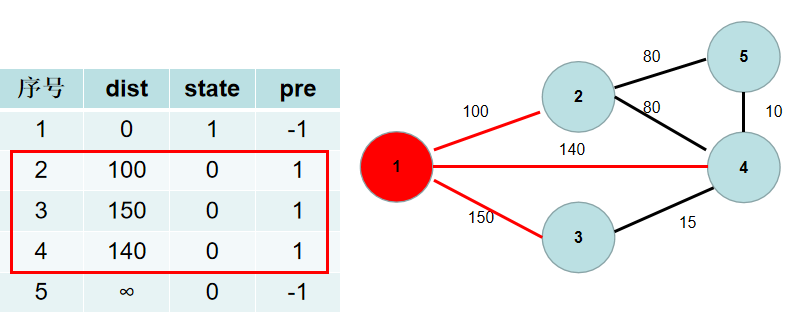 5. 重复 $3$, $4$步骤,直到所有节点的状态都被置为 $1$.
-这里青色点中距离最小的是 $dist[2]$,因此 $st[2]$ 置为 $1$。
+这里青色点中距离最小的是 $dis[2]$,因此 $st[2]$ 置为 $1$。
5. 重复 $3$, $4$步骤,直到所有节点的状态都被置为 $1$.
-这里青色点中距离最小的是 $dist[2]$,因此 $st[2]$ 置为 $1$。
+这里青色点中距离最小的是 $dis[2]$,因此 $st[2]$ 置为 $1$。
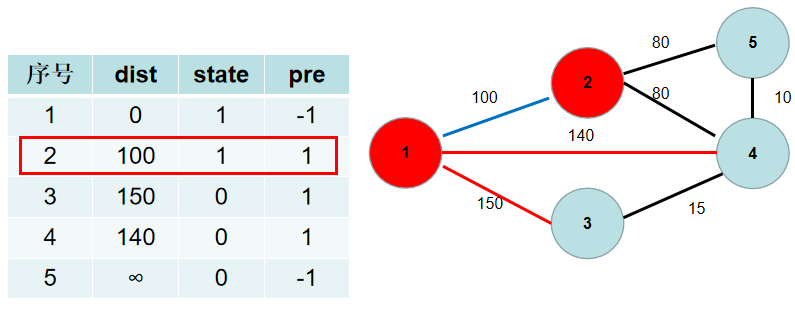 -与节点 $2$ 相连的有 $5$, $4$号节点。$2->5$ 的距离为 $80$,小于 $dist[5]$,$dist[5]$ 更新为 $80$,$pre[5]$ 更新为 $2$。$2->4$ 的距离为 $80$,小于 $dist[4]$,$dist[4]$ 更新为 $80$,$pre[4]$ 更新为$2$。
+与节点 $2$ 相连的有 $5$, $4$号节点。$2 \rightarrow 5$ 的距离为 $80$,小于 $dis[5]$,$dis[5]$ 更新为 $80$,$pre[5]$ 更新为 $2$。$2 \rightarrow 4$ 的距离为 $80$,小于 $dis[4]$,$dis[4]$ 更新为 $80$,$pre[4]$ 更新为$2$。
-与节点 $2$ 相连的有 $5$, $4$号节点。$2->5$ 的距离为 $80$,小于 $dist[5]$,$dist[5]$ 更新为 $80$,$pre[5]$ 更新为 $2$。$2->4$ 的距离为 $80$,小于 $dist[4]$,$dist[4]$ 更新为 $80$,$pre[4]$ 更新为$2$。
+与节点 $2$ 相连的有 $5$, $4$号节点。$2 \rightarrow 5$ 的距离为 $80$,小于 $dis[5]$,$dis[5]$ 更新为 $80$,$pre[5]$ 更新为 $2$。$2 \rightarrow 4$ 的距离为 $80$,小于 $dis[4]$,$dis[4]$ 更新为 $80$,$pre[4]$ 更新为$2$。
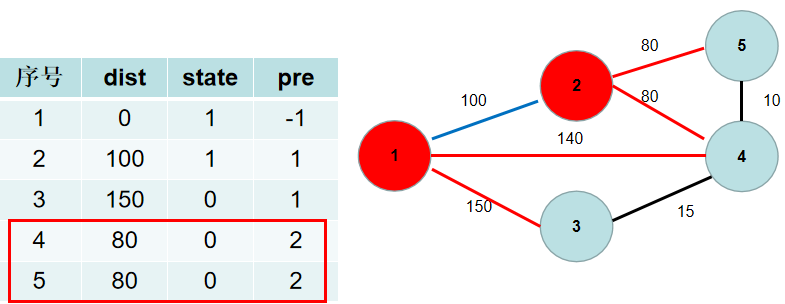 -选$dist[4]$,更新$dist[3]$,$dist[5]$,$pre[3]$,$pre[5]$。
+选$dis[4]$,更新$dis[3]$,$dis[5]$,$pre[3]$,$pre[5]$。
-选$dist[4]$,更新$dist[3]$,$dist[5]$,$pre[3]$,$pre[5]$。
+选$dis[4]$,更新$dis[3]$,$dis[5]$,$pre[3]$,$pre[5]$。
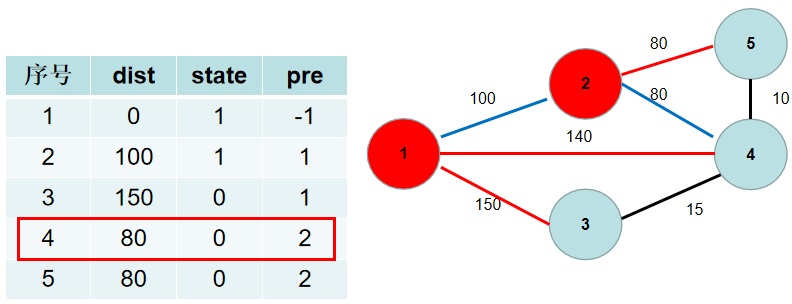
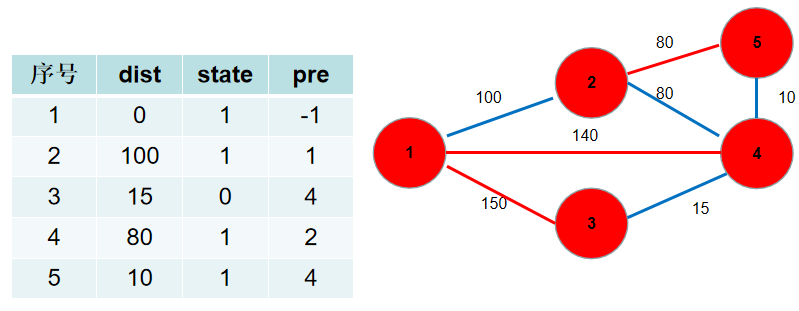
 -选$dist[5]$,没有可更新的。
+选$dis[5]$,没有可更新的。
-选$dist[5]$,没有可更新的。
+选$dis[5]$,没有可更新的。
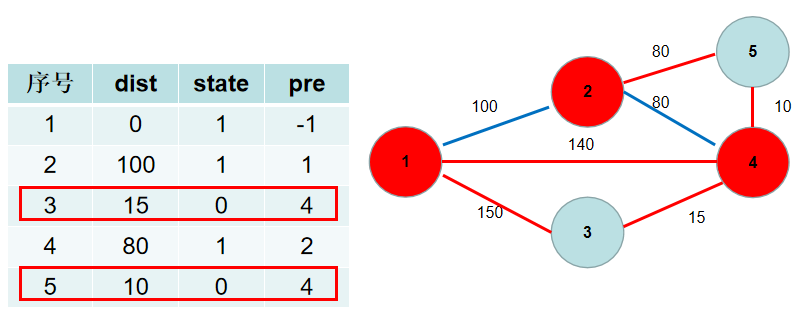
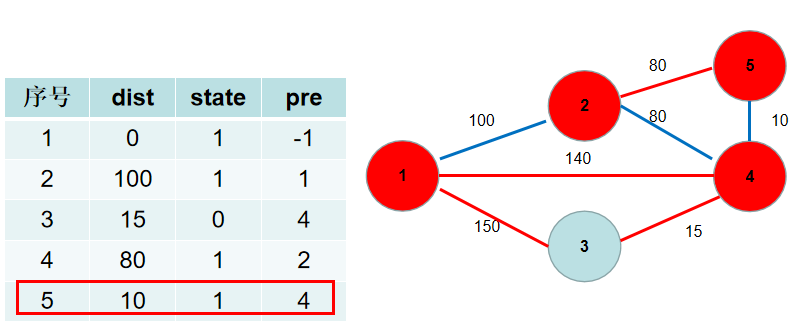 -选$dist[3]$,没有可更新的。
+选$dis[3]$,没有可更新的。
-选$dist[3]$,没有可更新的。
+选$dis[3]$,没有可更新的。
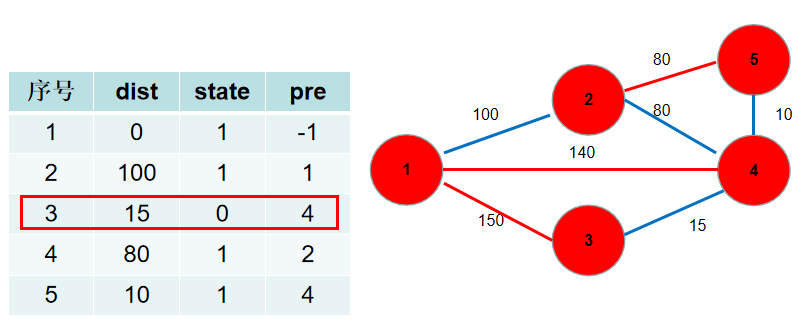 -6.此时 $dist$ 数组中保存了各个节点需要修的路长,加起来就是。$pre$ 数组中保存了需要选择的边。
+6.此时 $dis$ 数组中保存了各个节点需要修的路长,加起来就是。$pre$ 数组中保存了需要选择的边。
-6.此时 $dist$ 数组中保存了各个节点需要修的路长,加起来就是。$pre$ 数组中保存了需要选择的边。
+6.此时 $dis$ 数组中保存了各个节点需要修的路长,加起来就是。$pre$ 数组中保存了需要选择的边。
 @@ -119,8 +119,6 @@ $prim$ 算法采用的是一种 **贪心** 的策略,每次将离连通部分的
- 最小生成树并不唯一,但它的边权最小值是唯一的。所以,一般没有要求求出最小生成树长成什么样子,而是要求输出最小生成树的边权最小值。
- 因为$Prim$算法需要反复的求每两个点之间的距离,这就决定了 **邻接矩阵更合适**,因为**相对于邻接表,邻接矩阵可以快速提供两个点之间的距离**,而邻接表是链表,想要获取两个点之间的距离就没那么方便。
- 边数较少可以用$Kruskal$,因为$Kruskal$算法每次查找最短的边。 边数较多可以用$Prim$,因为它是每次加一个顶点,对边数多的适用。
-- 堆优化的$Prim$算法一般不用。
-- 图论的题一般难就难在建图上,考虑算法原理的并不多啊,所以理解并背下来算法模板的思路就非常重要了,主要是用自然语言复述,不要死记硬背模板代码,那样容易忘,也记不住。
### 四、朴素版$Prim$算法代码
@@ -152,7 +150,7 @@ int prim() {
/*2、如果不是第一个点,并且剩余的点距离集合的最小距离是INF,说明现在没有点可以连通到生成树,
这时不是连通图,没有最小生成树,返回INF
- 如果是第一个点,因为把它加到集合中去的代码是在下面进行的,此时它也没有被加入到集合中去,所以dist[t]=INF,这时不能说无解
+ 如果是第一个点,因为把它加到集合中去的代码是在下面进行的,此时它也没有被加入到集合中去,所以dis[t]=INF,这时不能说无解
因为才刚刚开始,需要特判一下
*/
if (i && dis[t] == INF) return INF;
diff --git a/TangDou/AcWing/MinimalSpanningTree/859.cpp b/TangDou/AcWing/MinimalSpanningTree/859.cpp
index 00649e6..94467d6 100644
--- a/TangDou/AcWing/MinimalSpanningTree/859.cpp
+++ b/TangDou/AcWing/MinimalSpanningTree/859.cpp
@@ -1,35 +1,42 @@
#include
using namespace std;
-
+const int N = 100010, M = N << 1;
const int INF = 0x3f3f3f3f;
+
int n, m; // n条顶点,m条边
int res; // 最小生成树的权值和
-int cnt; // 组成最小生成树的结点数
+int cnt; // 最小生成树的结点数
+
// Kruskal用到的结构体
-const int N = 100010, M = N << 1;
struct Node {
- int a, b, w;
- bool const operator<(const Node &ed) const {
- return w < ed.w;
+ int a, b, c;
+ bool const operator<(const Node &t) const {
+ return c < t.c; // 边权小的在前
}
-} edge[M];
+} edge[M]; // 数组长度为是边数
+
// 并查集
int p[N];
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
+
// Kruskal算法
int kruskal() {
+ // 1、按边权由小到大排序
sort(edge, edge + m);
+ // 2、并查集初始化
for (int i = 1; i <= n; i++) p[i] = i;
+ // 3、迭代m次
for (int i = 0; i < m; i++) {
- int a = edge[i].a, b = edge[i].b, w = edge[i].w;
+ int a = edge[i].a, b = edge[i].b, c = edge[i].c;
a = find(a), b = find(b);
if (a != b)
- p[a] = b, res += w, cnt++; // cnt是指已经连接上边的数量
+ p[a] = b, res += c, cnt++; // cnt是指已经连接上边的数量
}
+ // 4、特判是不是不连通
if (cnt < n - 1) return INF;
return res;
}
diff --git a/TangDou/AcWing/MinimalSpanningTree/859.md b/TangDou/AcWing/MinimalSpanningTree/859.md
index 80febfa..84141df 100644
--- a/TangDou/AcWing/MinimalSpanningTree/859.md
+++ b/TangDou/AcWing/MinimalSpanningTree/859.md
@@ -94,40 +94,47 @@ $A$:之所以使用邻接表或邻接矩阵,其实说白了,是按点存的
**按点存麻烦(邻接表或邻接矩阵),按边存(结构体数组)简单。**
-### 三、完整代码
+#### $Code$
```cpp {.line-numbers}
#include
using namespace std;
-
+const int N = 100010, M = N << 1;
const int INF = 0x3f3f3f3f;
+
int n, m; // n条顶点,m条边
int res; // 最小生成树的权值和
-int cnt; // 组成最小生成树的结点数
+int cnt; // 最小生成树的结点数
+
// Kruskal用到的结构体
-const int N = 100010, M = N << 1;
struct Node {
- int a, b, w;
- bool const operator<(const Node &ed) const {
- return w < ed.w;
+ int a, b, c;
+ bool const operator<(const Node &t) const {
+ return c < t.c; // 边权小的在前
}
-} edge[M];
+} edge[M]; // 数组长度为是边数
+
// 并查集
int p[N];
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
+
// Kruskal算法
int kruskal() {
+ // 1、按边权由小到大排序
sort(edge, edge + m);
+ // 2、并查集初始化
for (int i = 1; i <= n; i++) p[i] = i;
+ // 3、迭代m次
for (int i = 0; i < m; i++) {
- int a = edge[i].a, b = edge[i].b, w = edge[i].w;
+ int a = edge[i].a, b = edge[i].b, c = edge[i].c;
a = find(a), b = find(b);
if (a != b)
- p[a] = b, res += w, cnt++; // cnt是指已经连接上边的数量
+ p[a] = b, res += c, cnt++; // cnt是指已经连接上边的数量
}
+ // 4、特判是不是不连通
if (cnt < n - 1) return INF;
return res;
}
diff --git a/TangDou/Topic/【最小生成树】专题.md b/TangDou/Topic/【最小生成树】专题.md
index 4375281..a85512c 100644
--- a/TangDou/Topic/【最小生成树】专题.md
+++ b/TangDou/Topic/【最小生成树】专题.md
@@ -2,17 +2,153 @@
$Prim$算法和$Kruskal$算法都是用于 **求解最小生成树的算法**,但它们的使用场景和应用领域存在一些差异。
+### 一、算法概述
+
#### $Prim$算法
① $Prim$算法是一种贪心算法,基于顶点的方式构建最小生成树。
② $Prim$算法 **适用于稠密图**,即边的数量接近于完全图$(n*(n-1)/2)$的图。
③ $Prim$算法从一个起始顶点开始逐步扩展,直到生成一个包含所有顶点的最小生成树。
④ $Prim$算法的时间复杂度为$O(ElogV)$,对于稠密图有较好的性能。
+**[$AcWing$ $858$. $Prim$ 算法求最小生成树](https://www.cnblogs.com/littlehb/p/15330282.html)**
+
+**$Code$模板**
+```cpp {.line-numbers}
+#include
+
+using namespace std;
+const int N = 510;
+const int INF = 0x3f3f3f3f;
+
+int n, m;
+int g[N][N]; // 稠密图,邻接矩阵
+int dis[N]; // 这个点到集合的距离
+bool st[N]; // 是不是已经使用过
+int res; // 最小生成树里面边的长度之和
+int pre[N]; // 前驱结点
+
+// 普利姆算法求最小生成树
+int prim() {
+ for (int i = 0; i < n; i++) { // 迭代n次
+ int t = -1;
+ for (int j = 1; j <= n; j++)
+ if (!st[j] && (t == -1 || dis[t] > dis[j])) t = j;
+ if (i && dis[t] == INF) return INF; // 非连通图,没有最小生成树
+ if (i) res += dis[t];
+ for (int j = 1; j <= n; j++)
+ if (!st[j] && g[t][j] < dis[j]) {
+ dis[j] = g[t][j];
+ pre[j] = t; // 记录是由谁转移而来
+ }
+ st[t] = true;
+ }
+ return res;
+}
+
+int main() {
+ cin >> n >> m;
+ memset(g, 0x3f, sizeof g);
+ memset(dis, 0x3f, sizeof dis);
+ memset(pre, -1, sizeof pre); // 记录前驱路径
+
+ // 读入数据
+ while (m--) {
+ int a, b, c;
+ cin >> a >> b >> c;
+ g[a][b] = g[b][a] = min(g[a][b], c);
+ }
+ int t = prim();
+ if (t == INF)
+ puts("impossible");
+ else
+ cout << t << endl;
+
+ // 输出前驱结点
+ for (int i = 1; i <= n; i++) printf("%d ", pre[i]);
+ return 0;
+}
+```
#### $Kruskal$算法
① $Kruskal$算法是一种基于边的方式构建最小生成树的算法。
② $Kruskal$算法 **适用于稀疏图**,即边的数量远小于完全图$(n*(n-1)/2)$的图。
③ $Kruskal$算法按权值递增的顺序选择边,并通过判断是否构成环来决定是否将边加入最小生成树。
④ $Kruskal$算法的时间复杂度为$O(ElogE)$,对于稀疏图有较好的性能。
-#### 总结
-总体而言,$Prim$算法适用于稠密图,具有更好的时间复杂度,而$Kruskal$算法适用于稀疏图,具有相对较好的性能。在选择使用哪种算法时,可以根据图的特性和规模来进行选择。
+**[$AcWing$ $859$. $Kruskal$ 算法求最小生成树](https://www.cnblogs.com/littlehb/p/15336857.html)**
+
+**$Code$模板**
+```cpp {.line-numbers}
+#include
+
+using namespace std;
+const int N = 100010, M = N << 1;
+const int INF = 0x3f3f3f3f;
+
+int n, m; // n条顶点,m条边
+int res; // 最小生成树的权值和
+int cnt; // 最小生成树的结点数
+
+// Kruskal用到的结构体
+struct Node {
+ int a, b, c;
+ bool const operator<(const Node &t) const {
+ return c < t.c; // 边权小的在前
+ }
+} edge[M]; // 数组长度为是边数
+
+// 并查集
+int p[N];
+int find(int x) {
+ if (p[x] != x) p[x] = find(p[x]);
+ return p[x];
+}
+
+// Kruskal算法
+int kruskal() {
+ // 1、按边权由小到大排序
+ sort(edge, edge + m);
+ // 2、并查集初始化
+ for (int i = 1; i <= n; i++) p[i] = i;
+ // 3、迭代m次
+ for (int i = 0; i < m; i++) {
+ int a = edge[i].a, b = edge[i].b, c = edge[i].c;
+ a = find(a), b = find(b);
+ if (a != b)
+ p[a] = b, res += c, cnt++; // cnt是指已经连接上边的数量
+ }
+ // 4、特判是不是不连通
+ if (cnt < n - 1) return INF;
+ return res;
+}
+
+int main() {
+ cin >> n >> m;
+ for (int i = 0; i < m; i++) {
+ int a, b, c;
+ cin >> a >> b >> c;
+ edge[i] = {a, b, c};
+ }
+ int t = kruskal();
+ if (t == INF)
+ puts("impossible");
+ else
+ printf("%d\n", t);
+ return 0;
+}
+```
+
+### 二、最小生成树练习题题单
+
+
+AcWing 1140. 最短网络
+AcWing 1141. 局域网
+AcWing 1142. 繁忙的都市
+AcWing 1143. 联络员
+AcWing 1144. 连接格点
+
+
+### 三、最小生成树的扩展应用题单
+AcWing 1146. 新的开始
+AcWing 1145. 北极通讯网络
+AcWing 346. 走廊泼水节
+AcWing 1148. 秘密的牛奶运输
\ No newline at end of file
@@ -119,8 +119,6 @@ $prim$ 算法采用的是一种 **贪心** 的策略,每次将离连通部分的
- 最小生成树并不唯一,但它的边权最小值是唯一的。所以,一般没有要求求出最小生成树长成什么样子,而是要求输出最小生成树的边权最小值。
- 因为$Prim$算法需要反复的求每两个点之间的距离,这就决定了 **邻接矩阵更合适**,因为**相对于邻接表,邻接矩阵可以快速提供两个点之间的距离**,而邻接表是链表,想要获取两个点之间的距离就没那么方便。
- 边数较少可以用$Kruskal$,因为$Kruskal$算法每次查找最短的边。 边数较多可以用$Prim$,因为它是每次加一个顶点,对边数多的适用。
-- 堆优化的$Prim$算法一般不用。
-- 图论的题一般难就难在建图上,考虑算法原理的并不多啊,所以理解并背下来算法模板的思路就非常重要了,主要是用自然语言复述,不要死记硬背模板代码,那样容易忘,也记不住。
### 四、朴素版$Prim$算法代码
@@ -152,7 +150,7 @@ int prim() {
/*2、如果不是第一个点,并且剩余的点距离集合的最小距离是INF,说明现在没有点可以连通到生成树,
这时不是连通图,没有最小生成树,返回INF
- 如果是第一个点,因为把它加到集合中去的代码是在下面进行的,此时它也没有被加入到集合中去,所以dist[t]=INF,这时不能说无解
+ 如果是第一个点,因为把它加到集合中去的代码是在下面进行的,此时它也没有被加入到集合中去,所以dis[t]=INF,这时不能说无解
因为才刚刚开始,需要特判一下
*/
if (i && dis[t] == INF) return INF;
diff --git a/TangDou/AcWing/MinimalSpanningTree/859.cpp b/TangDou/AcWing/MinimalSpanningTree/859.cpp
index 00649e6..94467d6 100644
--- a/TangDou/AcWing/MinimalSpanningTree/859.cpp
+++ b/TangDou/AcWing/MinimalSpanningTree/859.cpp
@@ -1,35 +1,42 @@
#include
using namespace std;
-
+const int N = 100010, M = N << 1;
const int INF = 0x3f3f3f3f;
+
int n, m; // n条顶点,m条边
int res; // 最小生成树的权值和
-int cnt; // 组成最小生成树的结点数
+int cnt; // 最小生成树的结点数
+
// Kruskal用到的结构体
-const int N = 100010, M = N << 1;
struct Node {
- int a, b, w;
- bool const operator<(const Node &ed) const {
- return w < ed.w;
+ int a, b, c;
+ bool const operator<(const Node &t) const {
+ return c < t.c; // 边权小的在前
}
-} edge[M];
+} edge[M]; // 数组长度为是边数
+
// 并查集
int p[N];
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
+
// Kruskal算法
int kruskal() {
+ // 1、按边权由小到大排序
sort(edge, edge + m);
+ // 2、并查集初始化
for (int i = 1; i <= n; i++) p[i] = i;
+ // 3、迭代m次
for (int i = 0; i < m; i++) {
- int a = edge[i].a, b = edge[i].b, w = edge[i].w;
+ int a = edge[i].a, b = edge[i].b, c = edge[i].c;
a = find(a), b = find(b);
if (a != b)
- p[a] = b, res += w, cnt++; // cnt是指已经连接上边的数量
+ p[a] = b, res += c, cnt++; // cnt是指已经连接上边的数量
}
+ // 4、特判是不是不连通
if (cnt < n - 1) return INF;
return res;
}
diff --git a/TangDou/AcWing/MinimalSpanningTree/859.md b/TangDou/AcWing/MinimalSpanningTree/859.md
index 80febfa..84141df 100644
--- a/TangDou/AcWing/MinimalSpanningTree/859.md
+++ b/TangDou/AcWing/MinimalSpanningTree/859.md
@@ -94,40 +94,47 @@ $A$:之所以使用邻接表或邻接矩阵,其实说白了,是按点存的
**按点存麻烦(邻接表或邻接矩阵),按边存(结构体数组)简单。**
-### 三、完整代码
+#### $Code$
```cpp {.line-numbers}
#include
using namespace std;
-
+const int N = 100010, M = N << 1;
const int INF = 0x3f3f3f3f;
+
int n, m; // n条顶点,m条边
int res; // 最小生成树的权值和
-int cnt; // 组成最小生成树的结点数
+int cnt; // 最小生成树的结点数
+
// Kruskal用到的结构体
-const int N = 100010, M = N << 1;
struct Node {
- int a, b, w;
- bool const operator<(const Node &ed) const {
- return w < ed.w;
+ int a, b, c;
+ bool const operator<(const Node &t) const {
+ return c < t.c; // 边权小的在前
}
-} edge[M];
+} edge[M]; // 数组长度为是边数
+
// 并查集
int p[N];
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
+
// Kruskal算法
int kruskal() {
+ // 1、按边权由小到大排序
sort(edge, edge + m);
+ // 2、并查集初始化
for (int i = 1; i <= n; i++) p[i] = i;
+ // 3、迭代m次
for (int i = 0; i < m; i++) {
- int a = edge[i].a, b = edge[i].b, w = edge[i].w;
+ int a = edge[i].a, b = edge[i].b, c = edge[i].c;
a = find(a), b = find(b);
if (a != b)
- p[a] = b, res += w, cnt++; // cnt是指已经连接上边的数量
+ p[a] = b, res += c, cnt++; // cnt是指已经连接上边的数量
}
+ // 4、特判是不是不连通
if (cnt < n - 1) return INF;
return res;
}
diff --git a/TangDou/Topic/【最小生成树】专题.md b/TangDou/Topic/【最小生成树】专题.md
index 4375281..a85512c 100644
--- a/TangDou/Topic/【最小生成树】专题.md
+++ b/TangDou/Topic/【最小生成树】专题.md
@@ -2,17 +2,153 @@
$Prim$算法和$Kruskal$算法都是用于 **求解最小生成树的算法**,但它们的使用场景和应用领域存在一些差异。
+### 一、算法概述
+
#### $Prim$算法
① $Prim$算法是一种贪心算法,基于顶点的方式构建最小生成树。
② $Prim$算法 **适用于稠密图**,即边的数量接近于完全图$(n*(n-1)/2)$的图。
③ $Prim$算法从一个起始顶点开始逐步扩展,直到生成一个包含所有顶点的最小生成树。
④ $Prim$算法的时间复杂度为$O(ElogV)$,对于稠密图有较好的性能。
+**[$AcWing$ $858$. $Prim$ 算法求最小生成树](https://www.cnblogs.com/littlehb/p/15330282.html)**
+
+**$Code$模板**
+```cpp {.line-numbers}
+#include
+
+using namespace std;
+const int N = 510;
+const int INF = 0x3f3f3f3f;
+
+int n, m;
+int g[N][N]; // 稠密图,邻接矩阵
+int dis[N]; // 这个点到集合的距离
+bool st[N]; // 是不是已经使用过
+int res; // 最小生成树里面边的长度之和
+int pre[N]; // 前驱结点
+
+// 普利姆算法求最小生成树
+int prim() {
+ for (int i = 0; i < n; i++) { // 迭代n次
+ int t = -1;
+ for (int j = 1; j <= n; j++)
+ if (!st[j] && (t == -1 || dis[t] > dis[j])) t = j;
+ if (i && dis[t] == INF) return INF; // 非连通图,没有最小生成树
+ if (i) res += dis[t];
+ for (int j = 1; j <= n; j++)
+ if (!st[j] && g[t][j] < dis[j]) {
+ dis[j] = g[t][j];
+ pre[j] = t; // 记录是由谁转移而来
+ }
+ st[t] = true;
+ }
+ return res;
+}
+
+int main() {
+ cin >> n >> m;
+ memset(g, 0x3f, sizeof g);
+ memset(dis, 0x3f, sizeof dis);
+ memset(pre, -1, sizeof pre); // 记录前驱路径
+
+ // 读入数据
+ while (m--) {
+ int a, b, c;
+ cin >> a >> b >> c;
+ g[a][b] = g[b][a] = min(g[a][b], c);
+ }
+ int t = prim();
+ if (t == INF)
+ puts("impossible");
+ else
+ cout << t << endl;
+
+ // 输出前驱结点
+ for (int i = 1; i <= n; i++) printf("%d ", pre[i]);
+ return 0;
+}
+```
#### $Kruskal$算法
① $Kruskal$算法是一种基于边的方式构建最小生成树的算法。
② $Kruskal$算法 **适用于稀疏图**,即边的数量远小于完全图$(n*(n-1)/2)$的图。
③ $Kruskal$算法按权值递增的顺序选择边,并通过判断是否构成环来决定是否将边加入最小生成树。
④ $Kruskal$算法的时间复杂度为$O(ElogE)$,对于稀疏图有较好的性能。
-#### 总结
-总体而言,$Prim$算法适用于稠密图,具有更好的时间复杂度,而$Kruskal$算法适用于稀疏图,具有相对较好的性能。在选择使用哪种算法时,可以根据图的特性和规模来进行选择。
+**[$AcWing$ $859$. $Kruskal$ 算法求最小生成树](https://www.cnblogs.com/littlehb/p/15336857.html)**
+
+**$Code$模板**
+```cpp {.line-numbers}
+#include
+
+using namespace std;
+const int N = 100010, M = N << 1;
+const int INF = 0x3f3f3f3f;
+
+int n, m; // n条顶点,m条边
+int res; // 最小生成树的权值和
+int cnt; // 最小生成树的结点数
+
+// Kruskal用到的结构体
+struct Node {
+ int a, b, c;
+ bool const operator<(const Node &t) const {
+ return c < t.c; // 边权小的在前
+ }
+} edge[M]; // 数组长度为是边数
+
+// 并查集
+int p[N];
+int find(int x) {
+ if (p[x] != x) p[x] = find(p[x]);
+ return p[x];
+}
+
+// Kruskal算法
+int kruskal() {
+ // 1、按边权由小到大排序
+ sort(edge, edge + m);
+ // 2、并查集初始化
+ for (int i = 1; i <= n; i++) p[i] = i;
+ // 3、迭代m次
+ for (int i = 0; i < m; i++) {
+ int a = edge[i].a, b = edge[i].b, c = edge[i].c;
+ a = find(a), b = find(b);
+ if (a != b)
+ p[a] = b, res += c, cnt++; // cnt是指已经连接上边的数量
+ }
+ // 4、特判是不是不连通
+ if (cnt < n - 1) return INF;
+ return res;
+}
+
+int main() {
+ cin >> n >> m;
+ for (int i = 0; i < m; i++) {
+ int a, b, c;
+ cin >> a >> b >> c;
+ edge[i] = {a, b, c};
+ }
+ int t = kruskal();
+ if (t == INF)
+ puts("impossible");
+ else
+ printf("%d\n", t);
+ return 0;
+}
+```
+
+### 二、最小生成树练习题题单
+
+
+AcWing 1140. 最短网络
+AcWing 1141. 局域网
+AcWing 1142. 繁忙的都市
+AcWing 1143. 联络员
+AcWing 1144. 连接格点
+
+
+### 三、最小生成树的扩展应用题单
+AcWing 1146. 新的开始
+AcWing 1145. 北极通讯网络
+AcWing 346. 走廊泼水节
+AcWing 1148. 秘密的牛奶运输
\ No newline at end of file
 -2. 从 $1$ 号节点开始扩充连通的部分,[之所以从一号结点开始,是因为大家都是距离集合正无穷,那么号小的优先!],所以 $1$ 号节点与连通部分的最短距离为 $0$,即$dist[i]$ 值为 0。
+2. 从 $1$ 号节点开始扩充连通的部分,【之所以从一号结点开始,是因为大家都是距离集合正无穷,那么号小的优先!】,所以 $1$ 号节点与连通部分的最短距离为 $0$,即$dis[i]$ 值为 0。
-2. 从 $1$ 号节点开始扩充连通的部分,[之所以从一号结点开始,是因为大家都是距离集合正无穷,那么号小的优先!],所以 $1$ 号节点与连通部分的最短距离为 $0$,即$dist[i]$ 值为 0。
+2. 从 $1$ 号节点开始扩充连通的部分,【之所以从一号结点开始,是因为大家都是距离集合正无穷,那么号小的优先!】,所以 $1$ 号节点与连通部分的最短距离为 $0$,即$dis[i]$ 值为 0。
 -3. 遍历 $dist$ 数组,找到一个还没有连通起来,但是距离连通部分最近的点,假设该节点的编号是 $t$。$t$节点就是下一个应该加入连通部分的节点,$st[t]$ 置为 $true$。
-用青色点表示还没有连通起来的点,红色点表示连通起来的点。这里青色点中距离最小的是 $dist[1]$,因此 $st[1]$ 置为 $true$。
+3. 遍历 $dis$ 数组,找到一个还没有连通起来,但是距离连通部分最近的点,假设该节点的编号是 $t$。$t$节点就是下一个应该加入连通部分的节点,$st[t]$ 置为 $true$。
+用青色点表示还没有连通起来的点,红色点表示连通起来的点。这里青色点中距离最小的是 $dis[1]$,因此 $st[1]$ 置为 $true$。
-3. 遍历 $dist$ 数组,找到一个还没有连通起来,但是距离连通部分最近的点,假设该节点的编号是 $t$。$t$节点就是下一个应该加入连通部分的节点,$st[t]$ 置为 $true$。
-用青色点表示还没有连通起来的点,红色点表示连通起来的点。这里青色点中距离最小的是 $dist[1]$,因此 $st[1]$ 置为 $true$。
+3. 遍历 $dis$ 数组,找到一个还没有连通起来,但是距离连通部分最近的点,假设该节点的编号是 $t$。$t$节点就是下一个应该加入连通部分的节点,$st[t]$ 置为 $true$。
+用青色点表示还没有连通起来的点,红色点表示连通起来的点。这里青色点中距离最小的是 $dis[1]$,因此 $st[1]$ 置为 $true$。
 -4.遍历所有与 $t$ 相连但没有加入到连通部分的点 $j$,如果 $j$ 距离连通部分的距离大于 $t \sim j$ 之间的距离,即 $dist[j] > g[t][j]$($g[t][j]$ 为 $t \sim j$ 节点之间的距离),则更新 $dist[j]$ 为 $g[t][j]$。这时候表示,$j$ 到连通部分的最短方式是和 $t$ 相连,因此,更新$pre[j] = t$。
+4.遍历所有与 $t$ 相连但没有加入到连通部分的点 $j$,如果 $j$ 距离连通部分的距离大于 $t \sim j$ 之间的距离,即 $dis[j] > g[t][j]$($g[t][j]$ 为 $t \sim j$ 节点之间的距离),则更新 $dis[j]$ 为 $g[t][j]$。这时候表示,$j$ 到连通部分的最短方式是和 $t$ 相连,因此,更新$pre[j] = t$。
-与节点 $1$ 相连的有 $2$, $3$, $4$ 号节点。$1->2$ 的距离为 $100$,小于 $dist[2]$,$dist[2]$ 更新为 $100$,$pre[2]$ 更新为$1$。$1->4$ 的距离为 $140$,小于 $dist[4]$,$dist[4] $更新为 $140$,$pre[4]$ 更新为$1$。$1->3$ 的距离为 $150$,小于 $dist[3]$,$dist[3]$ 更新为 $150$,$pre[3]$ 更新为$1$。
+与节点 $1$ 相连的有 $2$, $3$, $4$ 号节点。$1 \rightarrow 2$ 的距离为 $100$,小于 $dis[2]$,$dis[2]$ 更新为 $100$,$pre[2]$ 更新为$1$。$1 \rightarrow 4$ 的距离为 $140$,小于 $dis[4]$,$dis[4] $更新为 $140$,$pre[4]$ 更新为$1$。$1 \rightarrow 3$ 的距离为 $150$,小于 $dis[3]$,$dis[3]$ 更新为 $150$,$pre[3]$ 更新为$1$。
-4.遍历所有与 $t$ 相连但没有加入到连通部分的点 $j$,如果 $j$ 距离连通部分的距离大于 $t \sim j$ 之间的距离,即 $dist[j] > g[t][j]$($g[t][j]$ 为 $t \sim j$ 节点之间的距离),则更新 $dist[j]$ 为 $g[t][j]$。这时候表示,$j$ 到连通部分的最短方式是和 $t$ 相连,因此,更新$pre[j] = t$。
+4.遍历所有与 $t$ 相连但没有加入到连通部分的点 $j$,如果 $j$ 距离连通部分的距离大于 $t \sim j$ 之间的距离,即 $dis[j] > g[t][j]$($g[t][j]$ 为 $t \sim j$ 节点之间的距离),则更新 $dis[j]$ 为 $g[t][j]$。这时候表示,$j$ 到连通部分的最短方式是和 $t$ 相连,因此,更新$pre[j] = t$。
-与节点 $1$ 相连的有 $2$, $3$, $4$ 号节点。$1->2$ 的距离为 $100$,小于 $dist[2]$,$dist[2]$ 更新为 $100$,$pre[2]$ 更新为$1$。$1->4$ 的距离为 $140$,小于 $dist[4]$,$dist[4] $更新为 $140$,$pre[4]$ 更新为$1$。$1->3$ 的距离为 $150$,小于 $dist[3]$,$dist[3]$ 更新为 $150$,$pre[3]$ 更新为$1$。
+与节点 $1$ 相连的有 $2$, $3$, $4$ 号节点。$1 \rightarrow 2$ 的距离为 $100$,小于 $dis[2]$,$dis[2]$ 更新为 $100$,$pre[2]$ 更新为$1$。$1 \rightarrow 4$ 的距离为 $140$,小于 $dis[4]$,$dis[4] $更新为 $140$,$pre[4]$ 更新为$1$。$1 \rightarrow 3$ 的距离为 $150$,小于 $dis[3]$,$dis[3]$ 更新为 $150$,$pre[3]$ 更新为$1$。
 5. 重复 $3$, $4$步骤,直到所有节点的状态都被置为 $1$.
-这里青色点中距离最小的是 $dist[2]$,因此 $st[2]$ 置为 $1$。
+这里青色点中距离最小的是 $dis[2]$,因此 $st[2]$ 置为 $1$。
5. 重复 $3$, $4$步骤,直到所有节点的状态都被置为 $1$.
-这里青色点中距离最小的是 $dist[2]$,因此 $st[2]$ 置为 $1$。
+这里青色点中距离最小的是 $dis[2]$,因此 $st[2]$ 置为 $1$。
 -与节点 $2$ 相连的有 $5$, $4$号节点。$2->5$ 的距离为 $80$,小于 $dist[5]$,$dist[5]$ 更新为 $80$,$pre[5]$ 更新为 $2$。$2->4$ 的距离为 $80$,小于 $dist[4]$,$dist[4]$ 更新为 $80$,$pre[4]$ 更新为$2$。
+与节点 $2$ 相连的有 $5$, $4$号节点。$2 \rightarrow 5$ 的距离为 $80$,小于 $dis[5]$,$dis[5]$ 更新为 $80$,$pre[5]$ 更新为 $2$。$2 \rightarrow 4$ 的距离为 $80$,小于 $dis[4]$,$dis[4]$ 更新为 $80$,$pre[4]$ 更新为$2$。
-与节点 $2$ 相连的有 $5$, $4$号节点。$2->5$ 的距离为 $80$,小于 $dist[5]$,$dist[5]$ 更新为 $80$,$pre[5]$ 更新为 $2$。$2->4$ 的距离为 $80$,小于 $dist[4]$,$dist[4]$ 更新为 $80$,$pre[4]$ 更新为$2$。
+与节点 $2$ 相连的有 $5$, $4$号节点。$2 \rightarrow 5$ 的距离为 $80$,小于 $dis[5]$,$dis[5]$ 更新为 $80$,$pre[5]$ 更新为 $2$。$2 \rightarrow 4$ 的距离为 $80$,小于 $dis[4]$,$dis[4]$ 更新为 $80$,$pre[4]$ 更新为$2$。
 -选$dist[4]$,更新$dist[3]$,$dist[5]$,$pre[3]$,$pre[5]$。
+选$dis[4]$,更新$dis[3]$,$dis[5]$,$pre[3]$,$pre[5]$。
-选$dist[4]$,更新$dist[3]$,$dist[5]$,$pre[3]$,$pre[5]$。
+选$dis[4]$,更新$dis[3]$,$dis[5]$,$pre[3]$,$pre[5]$。

 -选$dist[5]$,没有可更新的。
+选$dis[5]$,没有可更新的。
-选$dist[5]$,没有可更新的。
+选$dis[5]$,没有可更新的。
 -选$dist[3]$,没有可更新的。
+选$dis[3]$,没有可更新的。
-选$dist[3]$,没有可更新的。
+选$dis[3]$,没有可更新的。
 -6.此时 $dist$ 数组中保存了各个节点需要修的路长,加起来就是。$pre$ 数组中保存了需要选择的边。
+6.此时 $dis$ 数组中保存了各个节点需要修的路长,加起来就是。$pre$ 数组中保存了需要选择的边。
-6.此时 $dist$ 数组中保存了各个节点需要修的路长,加起来就是。$pre$ 数组中保存了需要选择的边。
+6.此时 $dis$ 数组中保存了各个节点需要修的路长,加起来就是。$pre$ 数组中保存了需要选择的边。
 @@ -119,8 +119,6 @@ $prim$ 算法采用的是一种 **贪心** 的策略,每次将离连通部分的
- 最小生成树并不唯一,但它的边权最小值是唯一的。所以,一般没有要求求出最小生成树长成什么样子,而是要求输出最小生成树的边权最小值。
- 因为$Prim$算法需要反复的求每两个点之间的距离,这就决定了 **邻接矩阵更合适**,因为**相对于邻接表,邻接矩阵可以快速提供两个点之间的距离**,而邻接表是链表,想要获取两个点之间的距离就没那么方便。
- 边数较少可以用$Kruskal$,因为$Kruskal$算法每次查找最短的边。 边数较多可以用$Prim$,因为它是每次加一个顶点,对边数多的适用。
-- 堆优化的$Prim$算法一般不用。
-- 图论的题一般难就难在建图上,考虑算法原理的并不多啊,所以理解并背下来算法模板的思路就非常重要了,主要是用自然语言复述,不要死记硬背模板代码,那样容易忘,也记不住。
### 四、朴素版$Prim$算法代码
@@ -152,7 +150,7 @@ int prim() {
/*2、如果不是第一个点,并且剩余的点距离集合的最小距离是INF,说明现在没有点可以连通到生成树,
这时不是连通图,没有最小生成树,返回INF
- 如果是第一个点,因为把它加到集合中去的代码是在下面进行的,此时它也没有被加入到集合中去,所以dist[t]=INF,这时不能说无解
+ 如果是第一个点,因为把它加到集合中去的代码是在下面进行的,此时它也没有被加入到集合中去,所以dis[t]=INF,这时不能说无解
因为才刚刚开始,需要特判一下
*/
if (i && dis[t] == INF) return INF;
diff --git a/TangDou/AcWing/MinimalSpanningTree/859.cpp b/TangDou/AcWing/MinimalSpanningTree/859.cpp
index 00649e6..94467d6 100644
--- a/TangDou/AcWing/MinimalSpanningTree/859.cpp
+++ b/TangDou/AcWing/MinimalSpanningTree/859.cpp
@@ -1,35 +1,42 @@
#include
@@ -119,8 +119,6 @@ $prim$ 算法采用的是一种 **贪心** 的策略,每次将离连通部分的
- 最小生成树并不唯一,但它的边权最小值是唯一的。所以,一般没有要求求出最小生成树长成什么样子,而是要求输出最小生成树的边权最小值。
- 因为$Prim$算法需要反复的求每两个点之间的距离,这就决定了 **邻接矩阵更合适**,因为**相对于邻接表,邻接矩阵可以快速提供两个点之间的距离**,而邻接表是链表,想要获取两个点之间的距离就没那么方便。
- 边数较少可以用$Kruskal$,因为$Kruskal$算法每次查找最短的边。 边数较多可以用$Prim$,因为它是每次加一个顶点,对边数多的适用。
-- 堆优化的$Prim$算法一般不用。
-- 图论的题一般难就难在建图上,考虑算法原理的并不多啊,所以理解并背下来算法模板的思路就非常重要了,主要是用自然语言复述,不要死记硬背模板代码,那样容易忘,也记不住。
### 四、朴素版$Prim$算法代码
@@ -152,7 +150,7 @@ int prim() {
/*2、如果不是第一个点,并且剩余的点距离集合的最小距离是INF,说明现在没有点可以连通到生成树,
这时不是连通图,没有最小生成树,返回INF
- 如果是第一个点,因为把它加到集合中去的代码是在下面进行的,此时它也没有被加入到集合中去,所以dist[t]=INF,这时不能说无解
+ 如果是第一个点,因为把它加到集合中去的代码是在下面进行的,此时它也没有被加入到集合中去,所以dis[t]=INF,这时不能说无解
因为才刚刚开始,需要特判一下
*/
if (i && dis[t] == INF) return INF;
diff --git a/TangDou/AcWing/MinimalSpanningTree/859.cpp b/TangDou/AcWing/MinimalSpanningTree/859.cpp
index 00649e6..94467d6 100644
--- a/TangDou/AcWing/MinimalSpanningTree/859.cpp
+++ b/TangDou/AcWing/MinimalSpanningTree/859.cpp
@@ -1,35 +1,42 @@
#include