|
|
|
|
@ -1320,37 +1320,47 @@ void dfs1(int u, int fa) {
|
|
|
|
|
|
|
|
|
|
现在考虑换根。
|
|
|
|
|
|
|
|
|
|
不难理解,如果$v \in son[u]$,换根时消去 $v$ 对 $u$ 的贡献,再将 $u$ 剩余贡献乘到 $ans[v]$ 上。
|
|
|
|
|
不难理解,如果$v \in son[u]$,换根时消去 $v$ 对 $u$ 的贡献,求出 $u$ 剩余贡献。
|
|
|
|
|
|
|
|
|
|
- 消去 $v$ 对 $u$ 的贡献:
|
|
|
|
|
|
|
|
|
|
$\large g[v]=\frac{f[u]}{f[v]+1}$
|
|
|
|
|
$\large x=\frac{f[u]}{f[v]+1}$
|
|
|
|
|
|
|
|
|
|
- 答案
|
|
|
|
|
|
|
|
|
|
$\large ans[v]=g[v] \times f[v]$
|
|
|
|
|
$\large g[v]=g[u] \times x$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
出现问题:**模数不保证是质数**,所以不能用直接乘逆元的方式来取模。
|
|
|
|
|
|
|
|
|
|
这里,对于每一个点 $u$,处理出 $f_{v∈son[u]}+1$ 的 **前缀积** 和 **后缀积**,即可解决求出消去一个子树贡献后的答案的问题。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
**除法与模的处理办法**
|
|
|
|
|
|
|
|
|
|
我们面对的是$g[v]=f[u]/(f[v]+1)$
|
|
|
|
|
我们面对的是$x=f[u]/(f[v]+1)$
|
|
|
|
|
|
|
|
|
|
求方案数由于数值太大,肯定会爆掉long long,题目也很 **温馨**(~~恶心~~)给出了使用对$mod$取模的办法进行规避$long$ $long$ 越界。按国际惯例,应该是一路计算过来一路取模,计算式子中出现了除法,联想到了逆元。但费马小定理求逆元要求模必须是质数,现在给定的mod可没有说必须是质数,所以,无法使用逆元来求解。
|
|
|
|
|
求方案数由于数值太大,肯定会爆掉$long$ $long$,题目也很 **温馨**(~~恶心~~)给出了使用对$mod$取模的办法进行规避$long$ $long$ 越界。按国际惯例,应该是一路计算过来一路取模,计算式子中出现了除法,联想到了逆元。但费马小定理求逆元要求模必须是质数,现在给定的$mod$可没有说必须是质数,所以,无法使用逆元来求解。
|
|
|
|
|
|
|
|
|
|
不让用除法逆元那怎么处理除法+取模呢?
|
|
|
|
|
答案就是:**前缀积+后缀积**!!
|
|
|
|
|
因为根据题意,$f[u]=(f[v1]+1)*(f[v2]+1)*(f[v3]+1)*(f[v4]+1)*....*$
|
|
|
|
|
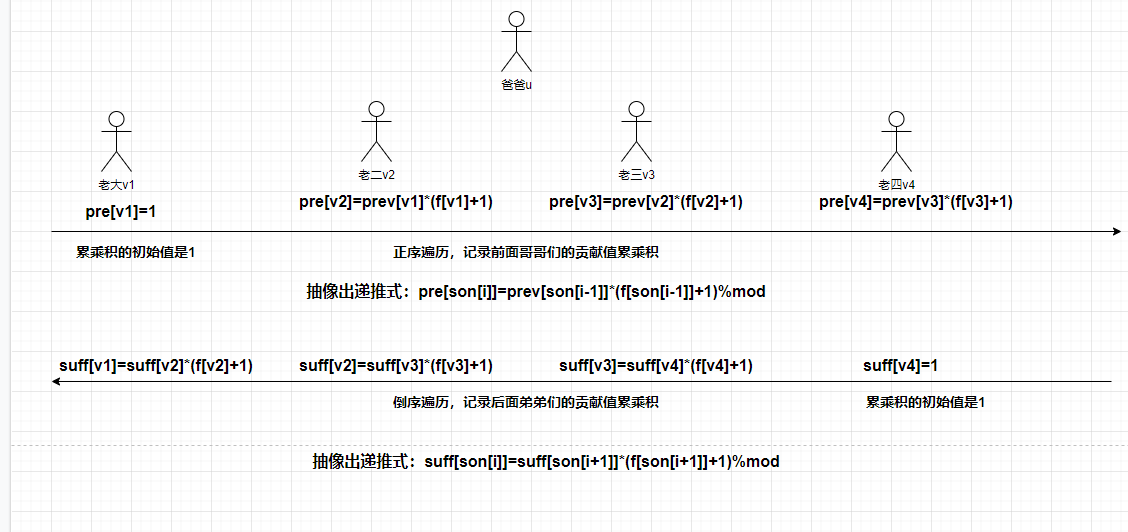
不让我用除法,我就不用除法,我只需要记录v的所有哥哥们的贡献乘积%$mod$,和,所以弟弟们的贡献乘积%$mod$,$pre[v]*suff[v]=f[u]/(f[v]+1)$
|
|
|
|
|
|
|
|
|
|
因为根据题意,$f[u]=(f[v_1]+1)*(f[v_2]+1)*(f[v_3]+1)*(f[v_4]+1)*....*$
|
|
|
|
|
不让我用除法,我就不用除法,我只需要记录$v$的所有哥哥们的贡献乘积%$mod$ 和 所有弟弟们的贡献乘积%$mod$:
|
|
|
|
|
|
|
|
|
|
$\large pre[v]*suff[v]=f[u]/(f[v]+1)$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 计算前缀积、后缀积的三种办法
|
|
|
|
|
|
|
|
|
|
<font color='red' size=4><b>总结:
|
|
|
|
|
① $f[u]$除掉$v$贡献,也就等于$v$节点的哥哥们贡献前缀积、弟弟们贡献后缀积
|
|
|
|
|
②
|
|
|
|
|
|
|
|
|
|
</font>
|
|
|
|
|
|
|
|
|
|
####
|
|
|
|
|
|
|
|
|
|
#### 计算前缀积、后缀积的三种办法
|
|
|
|
|
|
|
|
|
|
**方法$1$**
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|