diff --git a/TangDou/AcWing_TiGao/T5/GameTheory/1322.md b/TangDou/AcWing_TiGao/T5/GameTheory/1322.md
index 6de7731..4e47ff0 100644
--- a/TangDou/AcWing_TiGao/T5/GameTheory/1322.md
+++ b/TangDou/AcWing_TiGao/T5/GameTheory/1322.md
@@ -110,68 +110,70 @@ $\large L[i][i]=R[i][i]=a_i$
#### 分类讨论
+
+
- **特殊情况:$L=R=0$**
-令 $\displaystyle \large x=a[j](x>0)$
+令 $\displaystyle \large X=a[j](x>0)$
若 $R=0$ 则 $L=R=0$,此时 $x>\max\{L,R\}$,也就是说 $L=0$ 和 $R=0$ 都属于 $Case$ $5$,故其它 $Case$ 满足 $L,R>0$。
> 注:因$R=0$,表示在[$i$,$j-1$]确定后,右侧为$0$就能满足[$i$,$j-1$]这一段为先手必败,此时,左侧增加那堆个数为$0$就可以继续保持原来的先手必败,即$L=0$,而且已经证明了$L=R=0$是唯一的。
-* $x=R$($Case$ $1$)
- 最简单的情况——根据 $R=right[i][j-1]$ 的定义,$x=R$则区间 $[i,j]$ 是必败局面,因此左边啥也不能添,添了反而错,故
+* $X=R$($Case$ $1$)
+ 最简单的情况——根据 $R=right[i][j-1]$ 的定义,$X=R$则区间 $[i,j]$ 是必败局面,因此左边啥也不能添,添了反而错,故
$$\large left[i][j]=0$$
-* $x
- * $x \geq L$,即 $L \leq x < R$($Case$ $3$)
- * **结论**:$$\large left[i][j]=x+1$$
+ * ② $X \geq L$,即 $L \leq X < R$($Case$ $3$)
+ * **结论**:$$\large left[i][j]=X+1$$
* **证明**:
- 即 **求证** $(x+1,a_i,a_{i+1},\cdots,a_{j-1},x)$为 **必败局面** ,其中 $L \leq x L$,则后手将最右堆拿成 $z-1$ 个石子($z-1 \ge L>0$),**保证左侧比右侧多$1$个石子**,就能回到 $Case$ $3$ 本身,递归证明即可
* 若 $z=L$,则后手将最右堆拿完,根据 $L=left[i][j-1]$ 定义知此时局面必败
* 若 $0
* 若先手拿最右边一堆,设拿了以后 **还剩 $z$ 个石子**
* 若 $z \ge L$,则后手将最左堆拿成 $z+1$个石子,就能回到 $Case$ $3$ 本身,递归证明即可
* 若 $0R$
- * $x≤L$,即 $R < x \leq L$($Case$ $4$)
- * 结论:$$\large left[i][j]=x-1$$
+* $X>R$
+ * ① $X≤L$,即 $R < X \leq L$($Case$ $4$)
+ * 结论:$$\large left[i][j]=X-1$$
* **证明**:
* 若先手拿最左边一堆,设拿了以后还剩 $z$ 个石子。
- * 若 $z \geq R$,则后手将最右堆拿成 $z+1$ 个石子,保证左侧比右侧多$1$个石子,就能回到 $Case$ $4$ 本身,递归证明即可。
+ * 若 $z \geq R$,则后手将最右堆拿成 $z+1$ 个石子,保证左侧比右侧多$1$个石子,就能回到 $Case$ $4$ 本身,递归证明即可。
* 若 $0R$),由 $right[i][j-1])$ 的定义知此时是必败局面。
* 若先手拿最右边一堆,设拿了以后还剩 $z$ 个石子。
- * 若 $z>R$,则后手将最左边一堆拿成 $z-1$ 个石子(注意 $z-1 \ge R >0$),递归证明即可。保证右侧比左侧多$1$个石子。
+ * 若 $z>R$,则后手将最左边一堆拿成 $z-1$ 个石子(注意 $z-1 \ge R >0$),递归证明即可。保证右侧比左侧多$1$个石子。
* 若 $z=R$,则后手把最左堆拿完,根据 $right[i][j-1]$的定义可知得到了必败局面。
* 若 $0
- * $x>L$,即 $x>\max\{L,R\}$($Case$ $5$)
+ * ② $X>L$,即 $X>\max\{L,R\}$($Case$ $5$)
* **结论**:$$\large left[i][j]=x$$
* **证明**:
设先手将其中一堆拿成了 $z$ 个石子。
@@ -190,30 +192,30 @@ $\large L[i][i]=R[i][i]=a_i$
**综上所述:**
$$ \large
-L[i][j]=
+left[i][j]=
\large \left\{\begin{matrix}
- 0 & x=R \\
- x+1&L \leq x < R \\
-x-1 & R温馨提示:**请看清楚 $L$ 取不取等,乱取等是错的!**
-
-同理可求 $R(i,j)$。
+> 温馨提示:**请看清楚 $L$ 取不取等,乱取等是错的!**
-
-时间复杂度 $O(n^2)$。
+同理可求 $right(i,j)$。
### 六、实现代码
```cpp {.line-numbers}
#include
using namespace std;
+
const int N = 1010;
+
int n;
-int a[N], l[N][N], r[N][N];
+int a[N];
+int left[N][N], right[N][N];
int main() {
int T;
@@ -226,37 +228,37 @@ int main() {
for (int i = 1; i + len - 1 <= n; i++) {
int j = i + len - 1;
if (len == 1)
- l[i][j] = r[i][j] = a[i];
+ left[i][j] = right[i][j] = a[i];
else {
- int L = l[i][j - 1], R = r[i][j - 1], x = a[j];
- if (R == x)
- l[i][j] = 0;
- else if (x < L && x < R || x > L && x > R)
- l[i][j] = x;
+ int L = left[i][j - 1], R = right[i][j - 1], X = a[j];
+ if (R == X)
+ left[i][j] = 0;
+ else if (X < L && X < R || X > L && X > R)
+ left[i][j] = X;
else if (L > R)
- l[i][j] = x - 1;
+ left[i][j] = X - 1;
else
- l[i][j] = x + 1;
-
- // 与上述情况对称的四种情况
- L = l[i + 1][j], R = r[i + 1][j], x = a[i];
- if (L == x)
- r[i][j] = 0;
- else if (x < L && x < R || x > L && x > R)
- r[i][j] = x;
+ left[i][j] = X + 1;
+
+ L = left[i + 1][j], R = right[i + 1][j], X = a[i];
+ if (L == X)
+ right[i][j] = 0;
+ else if (X < L && X < R || X > L && X > R)
+ right[i][j] = X;
else if (R > L)
- r[i][j] = x - 1;
+ right[i][j] = X - 1;
else
- r[i][j] = x + 1;
+ right[i][j] = X + 1;
}
}
if (n == 1)
puts("1");
else
- printf("%d\n", l[2][n] != a[1]);
+ printf("%d\n", left[2][n] != a[1]);
}
return 0;
}
+
```
\ No newline at end of file
diff --git a/TangDou/AcWing_TiGao/T5/GameTheory/1322_2.md b/TangDou/AcWing_TiGao/T5/GameTheory/1322_2.md
deleted file mode 100644
index 2d86fae..0000000
--- a/TangDou/AcWing_TiGao/T5/GameTheory/1322_2.md
+++ /dev/null
@@ -1,175 +0,0 @@
-##[$AcWing 1322$. 取石子游戏](https://www.acwing.com/problem/content/1324/)
-
-### 一、题目描述
-在研究过 $Nim$ 游戏及各种变种之后,$Orez$ 又发现了一种全新的取石子游戏,这个游戏是这样的:
-
-有 $n$ 堆石子,将这 $n$ 堆石子摆成一排。
-
-游戏由两个人进行,两人轮流操作,每次操作者都可以从 **最左** 或 **最右** 的一堆中取出若干颗石子,可以将那一堆全部取掉,但不能不取,**不能操作的人就输了**。
-
-$Orez$ 问:对于任意给出的一个初始局面,是否存在先手必胜策略。
-
-**输入格式**
-第一行为一个整数 $T$,表示有 $T$ 组测试数据。
-
-对于每组测试数据,第一行为一个整数 $n$,表示有 $n$ 堆石子,第二行为 $n$ 个整数 $a_i$ ,依次表示每堆石子的数目。
-
-**输出格式**
-对于每组测试数据仅输出一个整数 $0$ 或 $1$,占一行。
-
-其中 $1$ 表示有先手必胜策略,$0$ 表示没有。
-
-**数据范围**
-$1≤T≤10,1≤n≤1000,1≤a_i≤10^9$
-
-**输入样例**:
-```cpp {.line-numbers}
-1
-4
-3 1 9 4
-```
-输出样例:
-```cpp {.line-numbers}
-0
-```
-
-### 二、思考过程
-
-#### 1、状态定义
-
-① 设 $left[i][j]$ 表示在 $[i,j]$ 已经固定的区间 **左侧** 放上一堆数量为 $left[i][j]$ 的石子后,**先手必败**
-② 设 $right[i][j]$ 表示在 $[i,j]$ 已经固定的区间 **右侧** 放上一堆数量为 $right[i][j]$ 的石子后,**先手必败**
-
-即:$(left[i][j],\underbrace{a_i,a_{i+1},\cdots,a_j}_{a[i]\sim a[j]})$,$(\underbrace{a_i,a_{i+1},\cdots,a_j}_{a[i]\sim a[j]},right[i][j])$ 为 **先手必败** 局面
-
-有如下两个性质:
-
-#### 2、$left[i][j]$,$right[i][j]$一定存在
-**反证法**:
-假设不存在满足定义的 $left[i][j]$,则对于 **任意非负整数** $x$,有形如:
-
-$$\large \underbrace{x,a_i,a_{i+1},\cdots,a_j}_{A(x)}$$ 都为 **必胜局面** ,记为 $A(x)$ 局面。
-
-由于 $A(x)$ 为必胜局面,故从 $A(x)$ 局面 必然存在若干种办法一步可达必败局面。
-
-若从最左边一堆中拿,因为假设原因,不可能变成必败局面,因为这样得到的局面仍形如 $A(x)$。
-
-
-左边拿没用,只能考虑从右边拿(即从$a_j$里拿):
-
-于是设 $A(x)$ 一步可达的某个 **必败局面**为 $(x,a_i,a_{i+1},\cdots,a_{j-1},y)$,显然有 $0 \le y < a_j$。
-
-**由于 $x$ 有无限个,但 $y$ 只有 $a_j$种——根据抽屉原理,必然存在 $x_1,x_2(x_1 > x_2),y$ 满足 $(x_1,a_i,a_{i+1},\cdots,a_{j-1},y)$ 和 $(x_2,a_i,a_{i+1},\cdots,a_{j-1},y)$ 都是必败局面**。但这两个必败局面之间 **实际一步可达**(比如拿走$x_1-x_2$个),矛盾,假设不成立,原命题成立。
-
-#### 3、$left[i][j]$,$right[i][j]$必然唯一
-
-**反证法**:
-假设 $left(i,j)$ 不唯一,则存在非负整数 $x_1,x_2(x_1 \neq x_2)$,使得$(x_1,a_i,a_{i+1},⋯,a_{j−1},a_j)$ 和 $(x_2,a_i,a_{i+1},\cdots,a_{j-1},a_j)$ 均为必败局面,而 **第一个必败局面** 可以通过拿走左侧$x_1-x_2$个石子到达另一个 **必败局面** ,矛盾,假设不成立,原命题成立。
-
-#### 4、推论
-有了上面推的$left[i][j]$唯一性,得出一个有用的推论:
-**对于任意非负整数 $x \neq left(i,j)$,$\large (x,a_i,a_{i+1},\cdots,a_j)$为必胜局面**
-
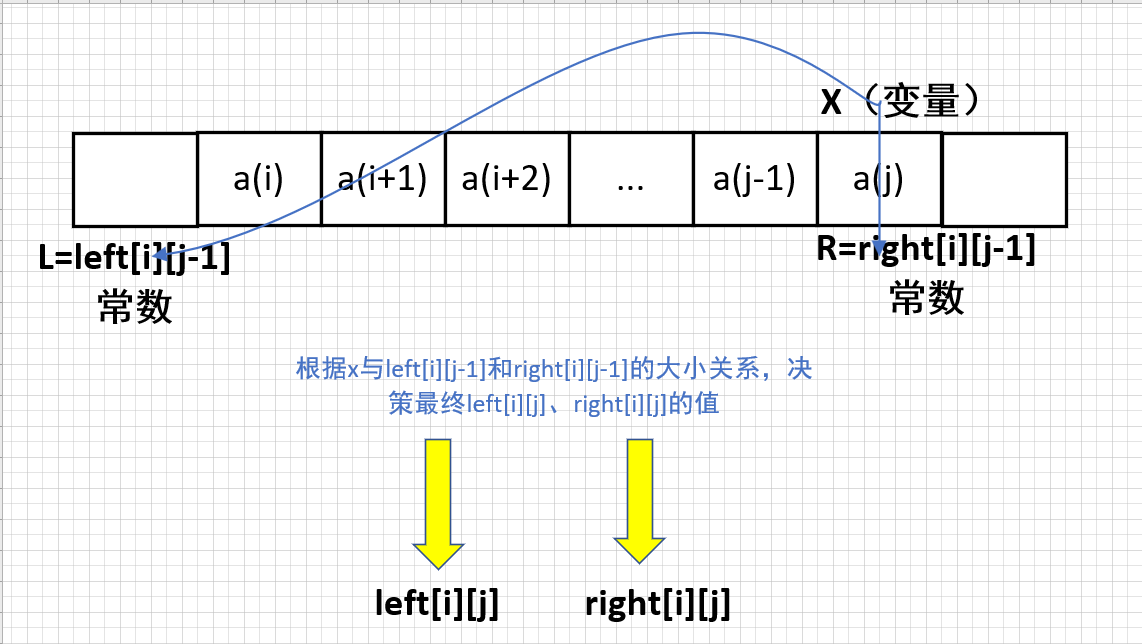
-#### 5、定义$L$和$R$
-因为下面的讨论中出现的$L$和$R$的含义不是很好理解,我们先把这个概念理清楚:
-
-
-
-
-**$Q$**:为什么要这么定义$L$和$R$呢?
-答:博弈论的题目都是可以通过动态规划来递推的。
-为什么呢?你想啊,最终的胜利,肯定不是从天下直接掉下来的,是一步步取得的,也就是前序状态会直接影响后面的状态,所以
-> **博弈论 $\Leftrightarrow $ 动态规划 $\Leftrightarrow $ 递归**
-
-递推嘛,就是类似于 **数学归纳法**,先求出初始状态是多少,然后假设$i \sim j-1$这段已经计算出$left[i][j-1],right[i][j-1]$了,现在想依赖于这两个数值推导出$left[i][j],right[i][j]$,怕写的太长麻烦,就定义了$L=left[i][j-1],R=right[i][j-1]$
-
-$left[i][j]$递推
-
-`?[i j-1] 第j堆(石子个数x)`
-则我们希望求的是假设$i\sim j$已经固定了,我们在左边放多少个可以使得`?[i j-1] 第j堆` 是必败的
-定义:
-左边放$L$时,`L[i j-1]`必败
-右边放$R$时,`[i j-1]R`必败
-
-
-**$Q$:那为什么是定义先手必败,而不是先手必胜呢?**
-答:因为上面证明过定义先手必败的动态规划数组,是肯定存在并且是唯一的,这样才能正常计算啊。
-
-考虑三个问题:
-- ① 初始值
-- ② 答案在哪
-- ③ 递推式
-> **注:答案在哪,并不是和递推式相关,而是和状态表示相关,一定要注意**
-
-
-**① 初始值**
-$\large L[i][i]=R[i][i]=a_i$
-
-当只有一堆石子时($only$ $i$),我在这堆前面添加一堆,个数和这堆一样多,对于**两堆相同的石子**,**后手进行和先手对称的操作**,你咋干我就咋干,我拿完,你瞪眼~, **先手必败**
-
-
-**② 答案在哪**
-**先手必败** $\Leftrightarrow \ L[2][n]=a_1$
-> **解释**:如果$L[2][n]$与$a[1]$相等,就意味着本来挺好的$a[2] \sim a[n]$,结果,前面放上了一个$a[1]$,而加上的$a[1]$使得现在的局面必败,先手必败。
-
-
-**③ 递推式**
-* 变化方法:从左侧拿走一些石子或者从右侧拿走一些石子
-
-
-
-
-### 六、实现代码
-```cpp {.line-numbers}
-#include
-
-using namespace std;
-const int N = 1010;
-int n;
-int a[N], l[N][N], r[N][N];
-
-int main() {
- int T;
- scanf("%d", &T);
- while (T--) {
- scanf("%d", &n);
- for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
-
- for (int len = 1; len <= n; len++)
- for (int i = 1; i + len - 1 <= n; i++) {
- int j = i + len - 1;
- if (len == 1)
- l[i][j] = r[i][j] = a[i];
- else {
- int L = l[i][j - 1], R = r[i][j - 1], x = a[j];
- if (R == x)
- l[i][j] = 0;
- else if (x < L && x < R || x > L && x > R)
- l[i][j] = x;
- else if (L > R)
- l[i][j] = x - 1;
- else
- l[i][j] = x + 1;
-
- // 与上述情况对称的四种情况
- L = l[i + 1][j], R = r[i + 1][j], x = a[i];
- if (L == x)
- r[i][j] = 0;
- else if (x < L && x < R || x > L && x > R)
- r[i][j] = x;
- else if (R > L)
- r[i][j] = x - 1;
- else
- r[i][j] = x + 1;
- }
- }
-
- if (n == 1)
- puts("1");
- else
- printf("%d\n", l[2][n] != a[1]);
- }
-
- return 0;
-}
-```
\ No newline at end of file