'commit'

TangDou/AcWing/Tree/1072_dfs_3.cpp

@@ -1,32 +1,33 @@
 #include <bits/stdc++.h>
 
 using namespace std;
+const int N = 10010, M = N << 1;
+int n; // n个结点
 
-const int N = 10010; // 点数上限
-const int M = N * 2; // 边数上限
-int n;
-int ans;
-int d1[N], d2[N]; // 最长，次长
-int st[N];
+// 链式前向星
 int h[N], e[M], w[M], ne[M], idx;
 void add(int a, int b, int c) {
     e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
 }
 
+// 换根dp模板
+int ans;          // 答案,直径
+int d1[N], d2[N]; // d1[i],d2[i]:经过i点的最长,次长长度是多少
+bool st[N];       // 是不是遍历过了
 void dfs(int u) {
-    st[u] = 1;
+    st[u] = true;
     for (int i = h[u]; ~i; i = ne[i]) {
-        int j = e[i];
-        if (st[j]) continue;
+        int v = e[i];
+        if (st[v]) continue; // v点访问过了
 
-        // 走j子树,完成后，j子树中每个节点的d1[j],d2[j]都已经准备好，u节点可以直接利用
-        dfs(j);
+        // 走v子树,完成后，v子树中每个节点的d1[v],d2[v]都已经准备好，u节点可以直接利用
+        dfs(v);
 
-        // d1[u]:最长路径,d2[u]:次长路径
-        if (d1[j] + w[i] >= d1[u])
-            d2[u] = d1[u], d1[u] = d1[j] + w[i]; // 最长路转移
-        else if (d1[j] + w[i] > d2[u])
-            d2[u] = d1[j] + w[i]; // 次长路转移
+        // w[i]:u->v的路径长度,d1[u]:最长路径,d2[u]:次长路径
+        if (d1[v] + w[i] >= d1[u])               // v可以用来更新u的最大值
+            d2[u] = d1[u], d1[u] = d1[v] + w[i]; // 最长路转移
+        else if (d1[v] + w[i] > d2[u])
+            d2[u] = d1[v] + w[i]; // 次长路转移
     }
     // 更新结果
     ans = max(ans, d1[u] + d2[u]);
@@ -34,16 +35,13 @@ void dfs(int u) {
 
 int main() {
     cin >> n;
-    // 初始化邻接表
-    memset(h, -1, sizeof h);
-    for (int i = 1; i < n; i++) {
+    memset(h, -1, sizeof h);      // 初始化邻接表
+    for (int i = 1; i < n; i++) { // n-1条边
         int a, b, c;
         cin >> a >> b >> c;
-        add(a, b, c), add(b, a, c);
+        add(a, b, c), add(b, a, c); // 换根dp一般用于无向图
     }
-    // 任选一个点作为根节点
-    dfs(1);
-    // 输出答案
-    printf("%d", ans);
+    dfs(1); // 任选一个点作为根节点,此处选择的是肯定存在的1号结点
+    cout << ans << endl;
     return 0;
 }

TangDou/Topic/【换根】dfs专题.md

@@ -1,9 +1,119 @@
 ## 换根 $dfs$ 专题 
 
+换根$DP$，又叫二次扫描，是树形$DP$的一种。
+
+其相比于一般的树形$DP$具有以下特点：
+
+- 以树上的不同点作为根，其解不同。
+- 故为求解答案，不能单求某点的信息，需要求解每个节点的信息。
+- 故无法通过一次搜索完成答案的求解，因为一次搜索只能得到一个节点的答案。
+难度也就要比一般的树形$DP$高一点。
+
+
+#### 题单
+$[POI2008]STA-Station$
+> **题意**：给定一个$n$个点的无根树，问以树上哪个节点为根时，其所有节点的深度和最大？
+**深度**：节点到根的简单路径上边的数量
+
+如果我们假设某个节点为根，将无根树化为有根树，在搜索回溯时统计子树的深度和，则可以用一次搜索算出以该节点为根时的深度和，其时间复杂度为 $O(N)$。
+
+但这样求解出的答案只是以该节点为根的，并不是最优解。
+
+如果要暴力求解出最优解，则我们可以枚举所有的节点为根，然后分别跑一次搜索，这样的时间复杂度会达到$O(N^2)$，显然不可接受。
+
+所以我们考虑在第二次搜索时就完成所有节点答案的统计——
+
+- ① 我们假设第一次搜索时的根节点为$1$号节点，则此时只有$1$号节点的答案是已知的。同时第一次搜索可以统计出所有子树的大小。
+- ② 第二次搜索依旧从$1$号节点出发，若$1$号节点与节点$x$相连，则我们考虑能否通过$1$号节点的答案去推出节点$x$的答案。
+
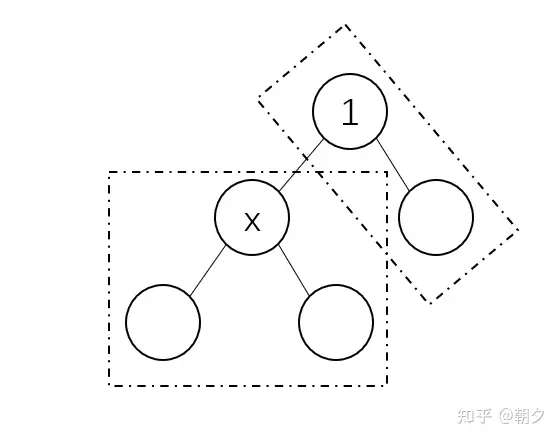
+- ③ 我们假设此时将根节点换成节点$x$，则其子树由两部分构成，第一部分是其原子树，第二部分则是$1$号节点的其他子树（如下图）。
+
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401090926001.png)
+
+- ④ 根从$1$号节点变为节点$x$的过程中，我们可以发现第一部分的深度降低了$1$，第二部分的深度则上升了$1$，而这两部分节点的数量在第一次搜索时就得到了。
+
+- ⑤ 故得到递推公式:
+$$ans[v]=ans[u]-siz[v]+(siz[1]-siz[v]),fa[v]=u$$
+化简一下，就是
+$$ans[v]=ans[u]+siz[1]-2\times siz[v]$$
+
+
+**总结与进阶**
+由此我们可以看出换根$DP$的套路：
+
+- 指定某个节点为根节点。
+- 第一次搜索完成预处理（如子树大小等），同时得到该节点的解。
+- 第二次搜索进行换根的动态规划，由已知解的节点推出相连节点的解。
+
+
+[USACO10MAR]Great Cow Gathering G
+
+
+CF1324F.Maximum White Subtree
+
+[USACO12FEB]Nearby Cows G
+
+[COCI2014-2015#1]Kamp
+
+[APIO2014]连珠线
+
+POJ3585 Accumulation Degree
+
+CF708C Centroids
 
 
 #### [$AcWing$ $1072$ 树的最长路径](https://www.cnblogs.com/littlehb/p/15784687.html)
 
+**$Code$**
+```cpp {.line-numbers}
+#include <bits/stdc++.h>
+
+using namespace std;
+const int N = 10010, M = N << 1;
+int n; // n个结点
+
+// 链式前向星
+int h[N], e[M], w[M], ne[M], idx;
+void add(int a, int b, int c) {
+    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
+}
+
+// 换根dp模板
+int ans;          // 答案,直径
+int d1[N], d2[N]; // d1[i],d2[i]:经过i点的最长,次长长度是多少
+bool st[N];       // 是不是遍历过了
+void dfs(int u) {
+    st[u] = true;
+    for (int i = h[u]; ~i; i = ne[i]) {
+        int v = e[i];
+        if (st[v]) continue; // v点访问过了
+
+        // 走v子树,完成后，v子树中每个节点的d1[v],d2[v]都已经准备好，u节点可以直接利用
+        dfs(v);
+
+        // w[i]:u->v的路径长度,d1[u]:最长路径,d2[u]:次长路径
+        if (d1[v] + w[i] >= d1[u])               // v可以用来更新u的最大值
+            d2[u] = d1[u], d1[u] = d1[v] + w[i]; // 最长路转移
+        else if (d1[v] + w[i] > d2[u])
+            d2[u] = d1[v] + w[i]; // 次长路转移
+    }
+    // 更新结果
+    ans = max(ans, d1[u] + d2[u]);
+}
+
+int main() {
+    cin >> n;
+    memset(h, -1, sizeof h);      // 初始化邻接表
+    for (int i = 1; i < n; i++) { // n-1条边
+        int a, b, c;
+        cin >> a >> b >> c;
+        add(a, b, c), add(b, a, c); // 换根dp一般用于无向图
+    }
+    dfs(1); // 任选一个点作为根节点,此处选择的是肯定存在的1号结点
+    cout << ans << endl;
+    return 0;
+}
+```
 #### [$AcWing$ $1073$. 树的中心](https://www.cnblogs.com/littlehb/p/15786805.html)
 
 #### [$AcWing$ $1148$ 秘密的牛奶运输](https://www.cnblogs.com/littlehb/p/16054005.html)