|
|
|
|
@ -685,68 +685,54 @@ int main() {
|
|
|
|
|
#### [$P3047$ $Nearby$ $Cows$ $G$](https://www.luogu.com.cn/problem/P3047)
|
|
|
|
|
|
|
|
|
|
**题目大意**
|
|
|
|
|
题目大意是给你一颗树,对于每一个节点$i$,求出范围$k$之内的点权之和。
|
|
|
|
|
|
|
|
|
|
看数据范围就知道暴力肯定是会$TLE$飞的,所以我们要考虑如何$dp$(代码习惯写$dfs$)
|
|
|
|
|
|
|
|
|
|
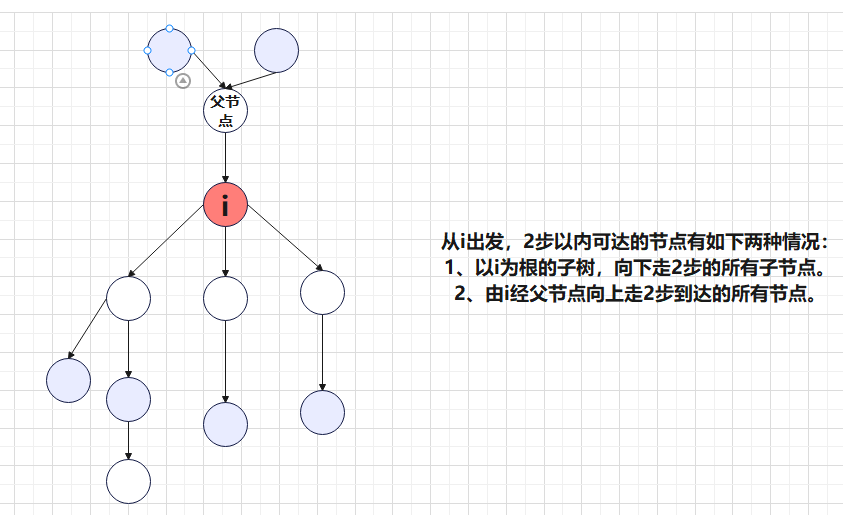
仔细思考一下我们发现点$i$走$k$步能到达的点分为以下两种:
|
|
|
|
|
|
|
|
|
|
- ① 在$i$的子树中(由$i$点往下)
|
|
|
|
|
- ② 经过$i$的父亲(由$i$点往上)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
这样的问题一般可以用两次$dfs$解决。
|
|
|
|
|
|
|
|
|
|
定义状态:
|
|
|
|
|
- $f[i][j]$表示$i$点往下$j$步范围内的点权之和
|
|
|
|
|
- $g[i][j]$表示$i$点往上和往下走$j$步范围内点权之和:【答案在这里】
|
|
|
|
|
|
|
|
|
|
第一次$dfs$我们求出所有的$f[i][k]$,这个简单,对于节点$u$和其儿子$v$:
|
|
|
|
|
|
|
|
|
|
**初始值**
|
|
|
|
|
$$f[i][0]=a[i]$$
|
|
|
|
|
> **解释**:每个节点,向下走$0$步,也就是一步不走,那还是它自己的点权,也就是$f[i][0]=a[i]$
|
|
|
|
|
|
|
|
|
|
**递推式**
|
|
|
|
|
$$f[u][j] = \sum_{v \in son[u]}f[v][j - 1]$$
|
|
|
|
|
|
|
|
|
|
第二次$dfs$我们通过已经求出的$f$数组推$g$数组,对于$u$和$v$,
|
|
|
|
|
$$g[v][k] += (g[u][k - 1] - f[v][k - 2])$$
|
|
|
|
|
|
|
|
|
|
----
|
|
|
|
|
|
|
|
|
|
题目简单地来说就是:
|
|
|
|
|
给你一棵 $n$ 个点的树,点带权,对于每个节点求出距离它不超过 $k$ 的所有节点权值和 $m_i$。
|
|
|
|
|
给你一棵 $n$ 个点的树,点带权,对于每个节点求出距离它不超过 $k$ 的所有节点权值和。
|
|
|
|
|
|
|
|
|
|
对于树中的某个节点而言,距离它不超过$k$的节点主要来源于两方面:
|
|
|
|
|
- 一个是该节点的子节点中距离该节点不超过距离$k$的节点的权值和
|
|
|
|
|
- 一个是该节点向上沿着父节点方向不超过距离$k$的点的权值和
|
|
|
|
|
|
|
|
|
|
对于子节点方向的节点的权值和,我们可以先通过普通的树形$DP$计算出来。
|
|
|
|
|
|
|
|
|
|
因此,我们先写一个$DP$计算出子树中距离该点不超过$k$的点的权值和。
|
|
|
|
|
对于子节点方向的节点的权值和,可以通过普通的树形$DP$计算出来。
|
|
|
|
|
|
|
|
|
|
**1、状态表示**
|
|
|
|
|
$f[u][k]$表示以$u$为根节点的树中,距离$u$不超过$k$的子节点的权值和。
|
|
|
|
|
$f[i][j]$表示以$i$为根节点的子树中,距离$i$不超过$j$的子节点的权值和。
|
|
|
|
|
|
|
|
|
|
**2、状态转移**
|
|
|
|
|
$$f[u][j]=val[u]+\sum_{v \in son[u]}f[v][j−1] \ j \in [1,k]$$
|
|
|
|
|
$$\large f[u][j]=val[u]+\sum_{v \in son[u]}f[v][j−1] \ j \in [1,k]$$
|
|
|
|
|
|
|
|
|
|
到节点$u$不超过距离$k$,即距离$son$不超过$k−1$,然后加在一起即可。同时$u$节点本身也是答案,因为$u$节点本身是不超过距离$0$的节点。
|
|
|
|
|
到节点$u$不超过距离$k$,即距离$v=son[u]$不超过$k−1$,然后加在一起即可。同时$u$节点本身也有贡献,因为$u$节点本身是不超过距离$0$的节点。
|
|
|
|
|
> **理解**:父亲的生活费=$\sum$(每个儿子给的生活费)+自己的社保金
|
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
void dfs1(int u, int fa) {
|
|
|
|
|
// 初始化:当遍历到u节点时,u的拆分状态中,最起码包含了自己的点权值
|
|
|
|
|
for (int i = 0; i <= k; i++) f[u][i] = val[u];
|
|
|
|
|
|
|
|
|
|
// 枚举u的每一个子节点
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
int v = e[i];
|
|
|
|
|
if (v == fa) continue; // 如果是u的父亲,那么就跳过,保证只访问u的孩子
|
|
|
|
|
// 先递归,// 递归填充v节点的信息
|
|
|
|
|
dfs1(v, u);
|
|
|
|
|
// 再利用子节点信息更新父节点信息
|
|
|
|
|
for (int j = 1; j <= k; j++) f[u][j] += f[v][j - 1];
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
**3、换根$DP$**
|
|
|
|
|
这个题目本身是个无根树,如果我们认为规定编号为$1$的节点是根的话,那么对于祖宗节点$1$来说,$f[1][k]$就是距离$1$节点不超过距离$k$的节点的权值和。因为祖宗节点是没有父亲节点的,所以我们就不需要考虑沿着父节点方向的节点权值和。
|
|
|
|
|
|
|
|
|
|
令:$g[u][k]$表示所有到$u$节点的不超过距离$k$的节点的权值和。根据刚刚的分析:$g[1][k]=f[1][k]$
|
|
|
|
|
令:$g[u][j]$表示所有到$u$节点的不超过距离$j$的节点的权值和。根据刚刚的分析:
|
|
|
|
|
$$\large g[1][j]=f[1][j]\ j \in [1,k]$$
|
|
|
|
|
|
|
|
|
|
这个就是我们换根$DP$的 **初始化**。其实受这个的启发,我们完全可以去把每个点都当作根,然后暴力跑出答案,但是这个暴力做法的时间复杂度是$O(n^2)$的,会超时。
|
|
|
|
|
这个就是我们换根$DP$的 **初始化**。
|
|
|
|
|
> **注**:我们完全可以去把每个点都当作根,然后暴力跑出答案,但是这个暴力做法的时间复杂度是$O(n^2)$的,会超时。
|
|
|
|
|
|
|
|
|
|
所以当我们将祖宗节点从节点$1$换为另一个节点的时候,我们只能通过数学上的关系来计算出$g$数组元素的值。这个也是换根$DP$的意义。
|
|
|
|
|
|
|
|
|
|
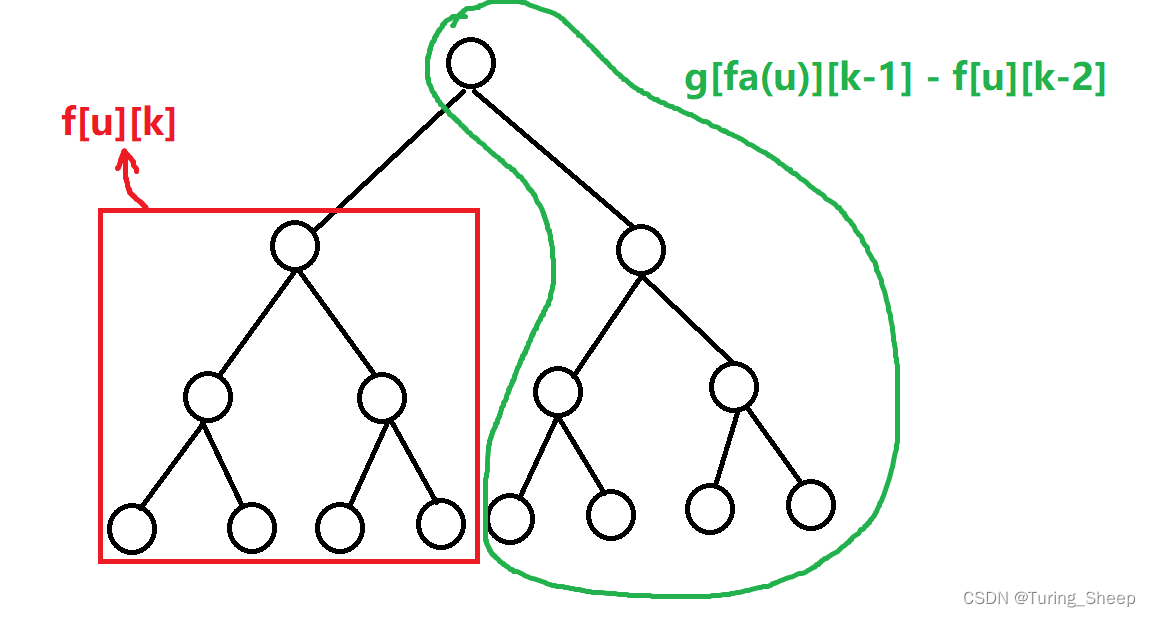
我们看下面的图:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
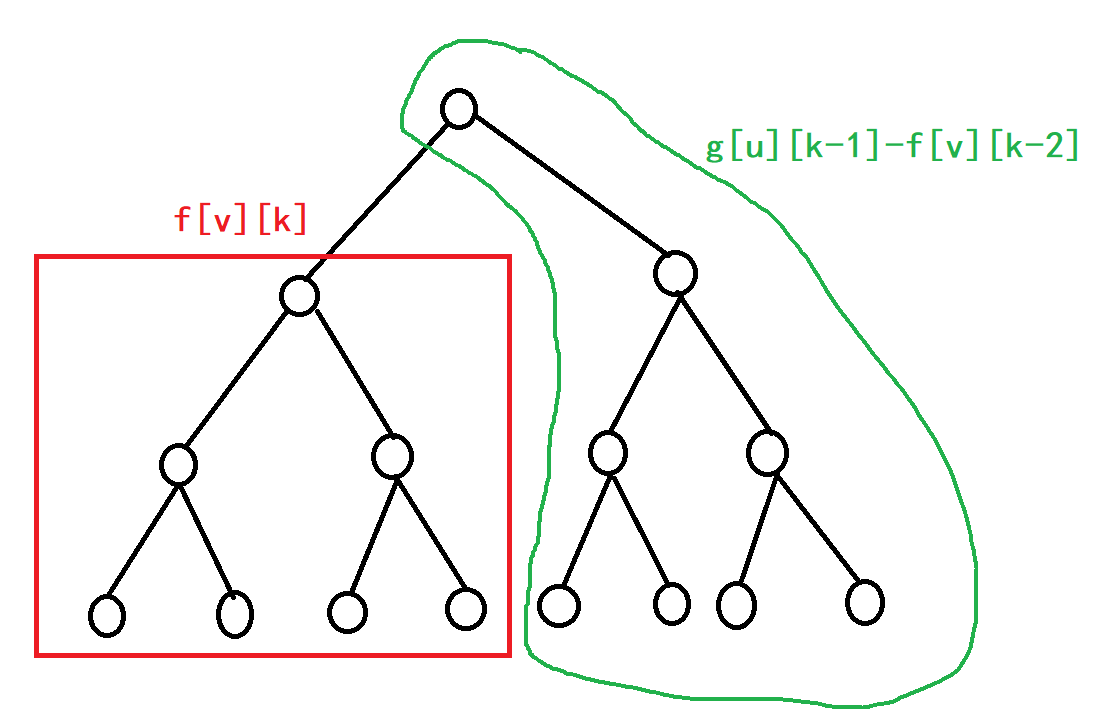
红色框是非常好理解的,以$v$为根的子树,在最远距离为$k$的限制下,写成$f[v][k]$。上面的部分,我们可以写成$g[u][k-1]$。因为到$v$不超过$k$的距离,即距离它的父亲节点不超过$k−1$的距离。
|
|
|
|
|
|
|
|
|
|
@ -759,14 +745,101 @@ $$f[u][j]=val[u]+\sum_{v \in son[u]}f[v][j−1] \ j \in [1,k]$$
|
|
|
|
|
所以最终的结果就是:
|
|
|
|
|
|
|
|
|
|
$$\large g[v][k]=f[v][k]+g[u][k−1]−f[v][k−2]$$
|
|
|
|
|
> **解释**:
|
|
|
|
|
> ① 换根$DP$时,由父推子,也就是用$g[u][?] \rightarrow g[v][??]$
|
|
|
|
|
> ② 由于$v$需要向上,通过$u$去寻找点权和,而$v \rightarrow u$已经用去了$1$步,一共$k$步,现在就剩下了$k-1$步。
|
|
|
|
|
> ③ $Q$:那为什么不是$f[u][k-1]$,而是$g[u][k-1]$呢?
|
|
|
|
|
> 因为$u$不光有向下的,还有向上的啊!我们现在不光要向下的,还要向上的,当然是$g[u][k-1]$啦!
|
|
|
|
|
> ④ 但是简单的这么整是不行的:$g[u][k-1]$与$f[v][k]$是存在交集的,如果简单加上就会造成一部分被算了两次!那么,是哪部分被算了两次呢?
|
|
|
|
|
> 答:对于$u$节点而言,$g[u][k-1]$与$f[v][k]$的交集,需要先走$1$步进入红框,这样,就用去了$1$步,也就是$f[v][k-2]$就是重复的部分,利用容斥原理去掉就行了,也就是$g[v][k]=f[v][k]+g[u][k−1]−f[v][k−2]$
|
|
|
|
|
|
|
|
|
|
细心的同学发现,这面的状态转移方程是有边界问题的:$k-2$是不是一定大于等于$0$呢?
|
|
|
|
|
如果$k-2<=0$咋办?会不会造成代码$RE$或者$WA$?
|
|
|
|
|
|
|
|
|
|
但是上述方程成立的条件是$k\geq 2$的。
|
|
|
|
|
也就是说,上述方程成立的条件是$k\geq 2$的。
|
|
|
|
|
|
|
|
|
|
所以我们还得想一想$\leq 1$的时候。
|
|
|
|
|
|
|
|
|
|
如果$k=0$,$g[u][0]$其实就是$val[u]$,因为不超过距离$0$的点只有本身。
|
|
|
|
|
如果$k=0$,$g[v][0]$其实就是$val[v]$,因为不超过距离$0$的点只有本身。
|
|
|
|
|
|
|
|
|
|
如果$k=1$,那么$g[v][1]$其实就是$f[v][1]+val[u]$,因为沿着父节点方向距离$v$不超过$1$的点,只有父节点,而树中,父节点是唯一的。沿着子节点方向,其实就是$v$的各个子节点,而这些子节点可以统统用$f[v][1]$表示。
|
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
using namespace std;
|
|
|
|
|
const int N = 1e5 + 10, M = N << 1;
|
|
|
|
|
const int K = 25;
|
|
|
|
|
// 链式前向星
|
|
|
|
|
int e[M], h[N], idx, w[M], ne[M];
|
|
|
|
|
void add(int a, int b, int c = 0) {
|
|
|
|
|
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
int f[N][K]; // f[i][j]:如果根是1号节点时,i号节点,最远走j步,可以获取到的所有点权和
|
|
|
|
|
int g[N][K];
|
|
|
|
|
int val[N]; // 点权数组
|
|
|
|
|
|
|
|
|
|
int n, k;
|
|
|
|
|
|
|
|
|
|
如果$k=1$,那么$g[u][1]$其实就是$f[u][1]+val[fa(u)]$,因为沿着父节点方向距离$u$不超过$1$的点,只有父节点,而树中,父节点是唯一的。沿着子节点方向,其实就是$u$的各个子节点,而这些子节点可以统统用$f[u][1]f[u][1]$表示。
|
|
|
|
|
void dfs1(int u, int fa) {
|
|
|
|
|
// 初始化:当遍历到u节点时,u的拆分状态中,最起码包含了自己的点权值
|
|
|
|
|
for (int i = 0; i <= k; i++) f[u][0] = val[u];
|
|
|
|
|
|
|
|
|
|
// 枚举u的每一个子节点
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
int v = e[i];
|
|
|
|
|
if (v == fa) continue; // 如果是u的父亲,那么就跳过,保证只访问u的孩子
|
|
|
|
|
|
|
|
|
|
// 递归,利用子更新父
|
|
|
|
|
dfs1(v, u); // 递归填充v节点的信息
|
|
|
|
|
// 在填充完子节点v的统计信息后,利用儿子们的填充信息,完成父亲节点信息的填充
|
|
|
|
|
// for(j=1,j<k,j++): 填充f[u]的每一个子状态,孩子们的j=1层汇集的数据,累加在一起就是f[u][j]的数据
|
|
|
|
|
// 最多计算k层足够用了
|
|
|
|
|
for (int j = 1; j <= k; j++) f[u][j] += f[v][j - 1];
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
// 换根dp
|
|
|
|
|
void dfs2(int u, int fa) {
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
int v = e[i];
|
|
|
|
|
if (v == fa) continue;
|
|
|
|
|
|
|
|
|
|
g[v][0] = val[v]; // 走0步,只有自己一个点
|
|
|
|
|
g[v][1] = f[v][1] + val[u]; // 走1步,包含自己下面子树一层+父节点
|
|
|
|
|
|
|
|
|
|
// 如果走2步及以上,最多k步以内
|
|
|
|
|
for (int j = 2; j <= k; j++) g[v][j] = f[v][j] + g[u][j - 1] - f[v][j - 2];
|
|
|
|
|
|
|
|
|
|
// 再递归,利用父更新子
|
|
|
|
|
dfs2(v, u);
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
int main() {
|
|
|
|
|
// 初始化链式前向星
|
|
|
|
|
memset(h, -1, sizeof h);
|
|
|
|
|
|
|
|
|
|
cin >> n >> k;
|
|
|
|
|
for (int i = 1; i < n; i++) { // n-1条边
|
|
|
|
|
int a, b;
|
|
|
|
|
cin >> a >> b;
|
|
|
|
|
add(a, b), add(b, a);
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
for (int i = 1; i <= n; i++) cin >> val[i]; // 点权
|
|
|
|
|
// 1、自底向上
|
|
|
|
|
dfs1(1, 0);
|
|
|
|
|
|
|
|
|
|
// 2、换根dp
|
|
|
|
|
for (int i = 0; i <= k; i++) g[1][i] = f[1][i];
|
|
|
|
|
dfs2(1, 0);
|
|
|
|
|
|
|
|
|
|
// 输出结果
|
|
|
|
|
for (int i = 1; i <= n; i++) cout << g[i][k] << endl;
|
|
|
|
|
return 0;
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
#### [$P6419$ $Kamp$](https://www.luogu.com.cn/problem/P6419)
|
|
|
|
|
https://www.cnblogs.com/Troverld/p/14601347.html
|
|
|
|
|
|