diff --git a/TangDou/AcWing/BeiBao/1023.md b/TangDou/AcWing/BeiBao/1023.md
index ea14993..0a410f2 100644
--- a/TangDou/AcWing/BeiBao/1023.md
+++ b/TangDou/AcWing/BeiBao/1023.md
@@ -3,11 +3,10 @@
**[【总结】背包问题的至多/恰好/至少](https://www.cnblogs.com/littlehb/p/15847138.html)**
### 一、题目描述
-小明有 $m$ 块钱,现有 $10$ 元, $20$ 元, $50$ 元, $100$ 元 的书
+小明有 $n$ 块钱全部用来买书,现有 $10$ 元, $20$ 元, $50$ 元, $100$ 元 的书
-每本书可以 **购买多次**,求小明有 **多少种** 买书 **方案**
+每本书可以 **购买多次**,求小明有 **多少种** 买书 **方案**,(每种书可购买多本)
-注:钱需要花完
**输入格式**
@@ -77,7 +76,7 @@ $0≤n≤1000$
 -### 二、朴素版本
+### 二、原始朴素版本
时间复杂度:$O(n^2 \times m)$
```cpp {.line-numbers}
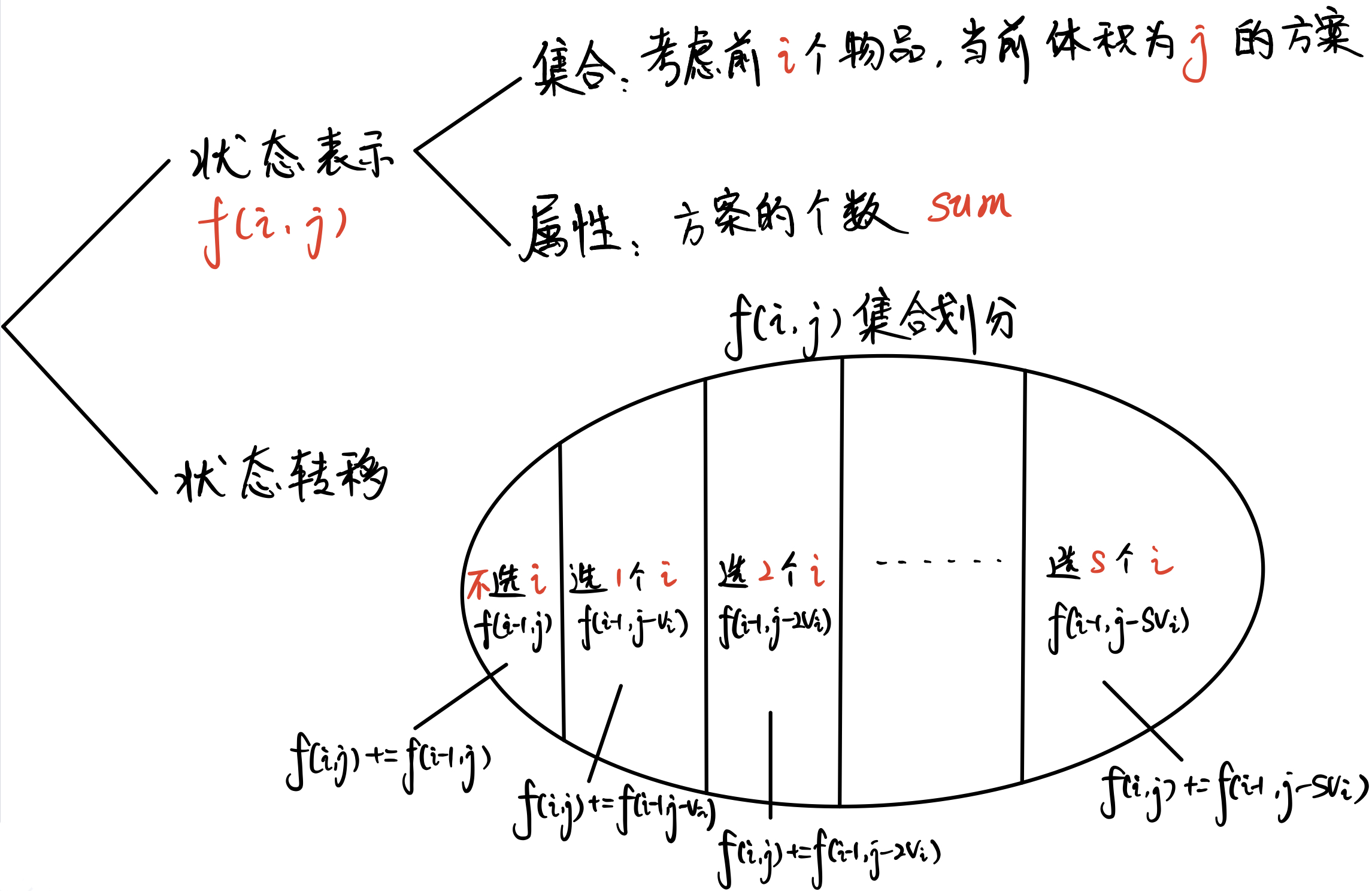
@@ -120,8 +119,8 @@ $$\large f(i,j-v_i)= f(i-1,j-v_i)+...+f(i-1,j-s\cdot v_i)②$$
注:把体积$j-v_i$代入①式,就可以得到 ②式
-$Q:$①和②中的$s$是一个值吗,为什么?
-答:是一个值的。原因可以从事情本质出发,思考一下$s\cdot v_i$的含义是什么:就是在$j$这么大的空间限制下,最多可以装多少个$i$物品,当然是同一个个数值$s$了。
+$Q:$①和②中的$s$是一个值吗?
+**答**:是一个值的。从事情本质出发,思考一下$s\cdot v_i$的含义:在$j$这么大的空间限制下,最多可以装多少个$i$物品,当然是同一个个数值$s$了。
由上述两个等式可以获得如下递推式:
diff --git a/TangDou/AcWing/BeiBao/3.md b/TangDou/AcWing/BeiBao/3.md
index a3f59da..7050b43 100644
--- a/TangDou/AcWing/BeiBao/3.md
+++ b/TangDou/AcWing/BeiBao/3.md
@@ -1,7 +1,7 @@
## [$AcWing$ $3$. 完全背包问题](https://www.acwing.com/problem/content/description/3/)
### 一、题目描述
-有 $N$ 种物品和一个容量是 $V$ 的背包,每种物品都有无限件可用。
+有 $N$ 种物品和一个容量是 $V$ 的背包,每种物品都有 **无限件** 可用。
第 $i$ 种物品的体积是 $v_i$,价值是 $w_i$。
diff --git a/TangDou/AcWing/BeiBao/Test.cpp b/TangDou/AcWing/BeiBao/Test.cpp
deleted file mode 100644
index c144829..0000000
--- a/TangDou/AcWing/BeiBao/Test.cpp
+++ /dev/null
@@ -1,37 +0,0 @@
-#include
-#define v first
-#define w second
-using namespace std;
-typedef pair PII;
-const int N = 70, M = 30010;
-int n, m, f[M];
-PII master[N];
-vector servent[N];
-int main() {
- cin >> m >> n;
- for (int i = 1; i <= n; i++) {
- int v, w, q;
- cin >> v >> w >> q;
- if (q == 0)
- master[i] = {v, v * w};
- else
- servent[q].push_back({v, v * w});
- }
- for (int i = 1; i <= n; i++)
- if (master[i].v) {
- for (int j = m; j >= 0; j--) {
- auto &sv = servent[i];
- for (int k = 0; k < 1 << sv.size(); k++) {
- int v = master[i].v, w = master[i].w;
- for (int u = 0; u < sv.size(); u++)
- if (k >> u & 1) {
- v += sv[u].v;
- w += sv[u].w;
- }
- if (j >= v) f[j] = max(f[j], f[j - v] + w);
- }
- }
- }
- cout << f[m] << endl;
- return 0;
-}
diff --git a/TangDou/AcWing/BeiBao/背包问题专题.md b/TangDou/AcWing/BeiBao/背包问题专题.md
index b93c215..24756f5 100644
--- a/TangDou/AcWing/BeiBao/背包问题专题.md
+++ b/TangDou/AcWing/BeiBao/背包问题专题.md
@@ -171,3 +171,55 @@ int main() {
return 0;
}
```
+### 四、完全背包
+**[$AcWing$ $3$. 完全背包问题](https://www.acwing.com/problem/content/3/)**
+
+**二维写法**
+```cpp {.line-numbers}
+#include
+using namespace std;
+const int N = 1010;
+int n, m;
+int f[N][N];
+
+int main() {
+ cin >> n >> m;
+
+ for (int i = 1; i <= n; i++) {
+ int v, w;
+ cin >> v >> w;
+ for (int j = 1; j <= m; j++) {
+ f[i][j] = f[i - 1][j];
+ if (j >= v)
+ f[i][j] = max(f[i][j], f[i][j - v] + w);
+ }
+ }
+ printf("%d\n", f[n][m]);
+ return 0;
+}
+```
+**一维解法**
+```cpp {.line-numbers}
+#include
+
+using namespace std;
+const int N = 1010;
+int n, m;
+int f[N];
+
+// 完全背包问题
+int main() {
+ cin >> n >> m;
+ for (int i = 1; i <= n; i++) {
+ int v, w;
+ cin >> v >> w;
+ for (int j = v; j <= m; j++)
+ f[j] = max(f[j], f[j - v] + w);
+ }
+ printf("%d\n", f[m]);
+ return 0;
+}
+```
+
+### 五、完全背包之恰好装满
+**[$AcWing$ $1023$. 买书](https://www.acwing.com/problem/content/1025/)**
-### 二、朴素版本
+### 二、原始朴素版本
时间复杂度:$O(n^2 \times m)$
```cpp {.line-numbers}
@@ -120,8 +119,8 @@ $$\large f(i,j-v_i)= f(i-1,j-v_i)+...+f(i-1,j-s\cdot v_i)②$$
注:把体积$j-v_i$代入①式,就可以得到 ②式
-$Q:$①和②中的$s$是一个值吗,为什么?
-答:是一个值的。原因可以从事情本质出发,思考一下$s\cdot v_i$的含义是什么:就是在$j$这么大的空间限制下,最多可以装多少个$i$物品,当然是同一个个数值$s$了。
+$Q:$①和②中的$s$是一个值吗?
+**答**:是一个值的。从事情本质出发,思考一下$s\cdot v_i$的含义:在$j$这么大的空间限制下,最多可以装多少个$i$物品,当然是同一个个数值$s$了。
由上述两个等式可以获得如下递推式:
diff --git a/TangDou/AcWing/BeiBao/3.md b/TangDou/AcWing/BeiBao/3.md
index a3f59da..7050b43 100644
--- a/TangDou/AcWing/BeiBao/3.md
+++ b/TangDou/AcWing/BeiBao/3.md
@@ -1,7 +1,7 @@
## [$AcWing$ $3$. 完全背包问题](https://www.acwing.com/problem/content/description/3/)
### 一、题目描述
-有 $N$ 种物品和一个容量是 $V$ 的背包,每种物品都有无限件可用。
+有 $N$ 种物品和一个容量是 $V$ 的背包,每种物品都有 **无限件** 可用。
第 $i$ 种物品的体积是 $v_i$,价值是 $w_i$。
diff --git a/TangDou/AcWing/BeiBao/Test.cpp b/TangDou/AcWing/BeiBao/Test.cpp
deleted file mode 100644
index c144829..0000000
--- a/TangDou/AcWing/BeiBao/Test.cpp
+++ /dev/null
@@ -1,37 +0,0 @@
-#include
-#define v first
-#define w second
-using namespace std;
-typedef pair PII;
-const int N = 70, M = 30010;
-int n, m, f[M];
-PII master[N];
-vector servent[N];
-int main() {
- cin >> m >> n;
- for (int i = 1; i <= n; i++) {
- int v, w, q;
- cin >> v >> w >> q;
- if (q == 0)
- master[i] = {v, v * w};
- else
- servent[q].push_back({v, v * w});
- }
- for (int i = 1; i <= n; i++)
- if (master[i].v) {
- for (int j = m; j >= 0; j--) {
- auto &sv = servent[i];
- for (int k = 0; k < 1 << sv.size(); k++) {
- int v = master[i].v, w = master[i].w;
- for (int u = 0; u < sv.size(); u++)
- if (k >> u & 1) {
- v += sv[u].v;
- w += sv[u].w;
- }
- if (j >= v) f[j] = max(f[j], f[j - v] + w);
- }
- }
- }
- cout << f[m] << endl;
- return 0;
-}
diff --git a/TangDou/AcWing/BeiBao/背包问题专题.md b/TangDou/AcWing/BeiBao/背包问题专题.md
index b93c215..24756f5 100644
--- a/TangDou/AcWing/BeiBao/背包问题专题.md
+++ b/TangDou/AcWing/BeiBao/背包问题专题.md
@@ -171,3 +171,55 @@ int main() {
return 0;
}
```
+### 四、完全背包
+**[$AcWing$ $3$. 完全背包问题](https://www.acwing.com/problem/content/3/)**
+
+**二维写法**
+```cpp {.line-numbers}
+#include
+using namespace std;
+const int N = 1010;
+int n, m;
+int f[N][N];
+
+int main() {
+ cin >> n >> m;
+
+ for (int i = 1; i <= n; i++) {
+ int v, w;
+ cin >> v >> w;
+ for (int j = 1; j <= m; j++) {
+ f[i][j] = f[i - 1][j];
+ if (j >= v)
+ f[i][j] = max(f[i][j], f[i][j - v] + w);
+ }
+ }
+ printf("%d\n", f[n][m]);
+ return 0;
+}
+```
+**一维解法**
+```cpp {.line-numbers}
+#include
+
+using namespace std;
+const int N = 1010;
+int n, m;
+int f[N];
+
+// 完全背包问题
+int main() {
+ cin >> n >> m;
+ for (int i = 1; i <= n; i++) {
+ int v, w;
+ cin >> v >> w;
+ for (int j = v; j <= m; j++)
+ f[j] = max(f[j], f[j - v] + w);
+ }
+ printf("%d\n", f[m]);
+ return 0;
+}
+```
+
+### 五、完全背包之恰好装满
+**[$AcWing$ $1023$. 买书](https://www.acwing.com/problem/content/1025/)**

