|
|
|
|
@ -113,3 +113,185 @@ void get_mobius2(LL n) {
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
#### 6、性质
|
|
|
|
|
然后就谈谈它的两条性质:
|
|
|
|
|
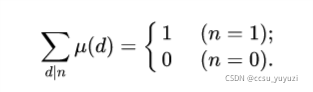
|
|
|
|
|
|
|
|
|
|
该图意为$n$的所有因子的莫比乌斯值的和只有在$n=1$时成立为$1$,其余通通为$0$;
|
|
|
|
|
|
|
|
|
|
对这个性质的证明:
|
|
|
|
|
|
|
|
|
|
首先我们可以把$n$分解为很多个质数相乘(此时质数的幂不一定为$1$):
|
|
|
|
|
令 $\large n=p_1^ {a_1}* p_2^ {a_2}* ... *p_k^{a_k}$
|
|
|
|
|
因为这是对它们的莫比乌斯值的求和,这是求它所有约数的莫比乌斯值的和,就相当于在这么多的素数中依次选择一个两个三个......的质因子来相乘组成所有约数,但是根据莫比乌斯函数性质,包含有素数平方的约数不用计算,他对答案的贡献值为$0$,所以我们可以把$n$分解的质数的次数全部消除为$1$,只有当莫比乌斯值为$-1$或者$1$时才对结果有贡献.那么问题就单纯的变为在$k$个$n$的质因子中选$0$到$k$个值组成约数,再将这些约数的值相加:
|
|
|
|
|
|
|
|
|
|
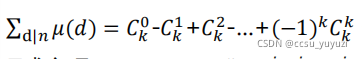
|
|
|
|
|
|
|
|
|
|
注意,这里的符号并不是全为加法,而是隔一个加隔一个减,这是因为莫比乌斯函数是积性函数,当选的数是奇数个时为值为负,反之为正,又因二项式定理,将$-1$和$1$带入,可以得到结果为$0$.
|
|
|
|
|
|
|
|
|
|
这里的式子就很像容斥定理了,那我顺便记录一下我理解的一小部分容斥定理:
|
|
|
|
|
|
|
|
|
|
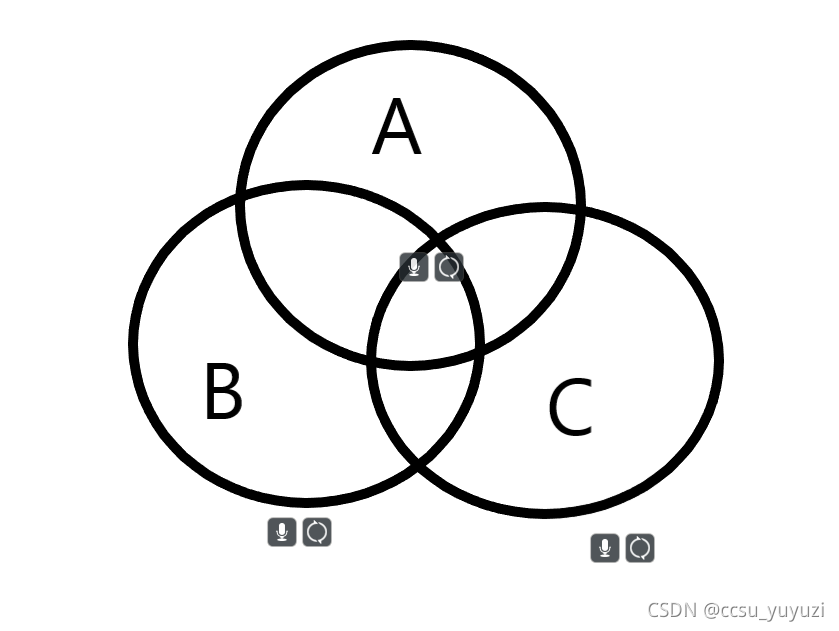
|
|
|
|
|
|
|
|
|
|
举个例子就好理解了,当我们要计算这个图形的面积,我们可以先计算$A,B,C$三个图形的面积的和,计算完之后我们会发现多计算了重叠部分,那么在尝试减去每两个相交的的图形的面积,这样每两两相交的面积被减去后,我们会发现,第一次算三个大面积时计算了三次的最中间的那个面积,在第二次减去两两相交的面积是有被减去了三次,就相当于没有计算了,这里就要再次加上最中间的这个面积,也就得到了图形总面积.大概就是这样的意思,当你计算某种含有多种性质的集合的时候(每个集合中元素可能有很多种性质),就可以这样计算.(其实还不是太懂,在下面例题的时候会有运用,它和莫比乌斯函数值的分布非常像).
|
|
|
|
|
|
|
|
|
|
(2)对任意正整数n
|
|
|
|
|
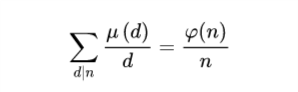
|
|
|
|
|
|
|
|
|
|
(ps:这条涉及莫比乌斯反演,还没学,学了再看)
|
|
|
|
|
|
|
|
|
|
好了,这就是大致知识,我学完了这个还是不知道这东西到底有什么用,还是得靠实战:
|
|
|
|
|
|
|
|
|
|
例题:[完全平方数](https://www.luogu.com.cn/problem/P4318)
|
|
|
|
|
|
|
|
|
|
题意就是筛去完全平方数及其的倍数,然后输出第k个的值.
|
|
|
|
|
|
|
|
|
|
我们要求这个,就想到把1到ki的所有完全平方数和他的倍数筛去,但是一看数据,1e9,线性筛必定t,那再去想办法进行计算,我们先把2的平方4的倍数计算出来,在1到ki中,有ki/4个4的倍数,我们再计算的16的倍数个数时候,会发现在计算4的倍数个数时候已经把16的倍数个数计算过了,这里就重复了,而假设已经计算了4和9的倍数个数,再去计算36的倍数个数就会发现计算了两次,那么就要减去36的倍数个数,这里就已经想到可以用容斥了.这里我们发现这里需要枚举质数的平方的次数,且奇数偶数符号不相同,就会想到莫比乌斯函数.它计算枚举的边界是i*i<=n;我们再用n减去计算的出来的从2开始的到ki的完全平方数的个数即为所求:
|
|
|
|
|
|
|
|
|
|
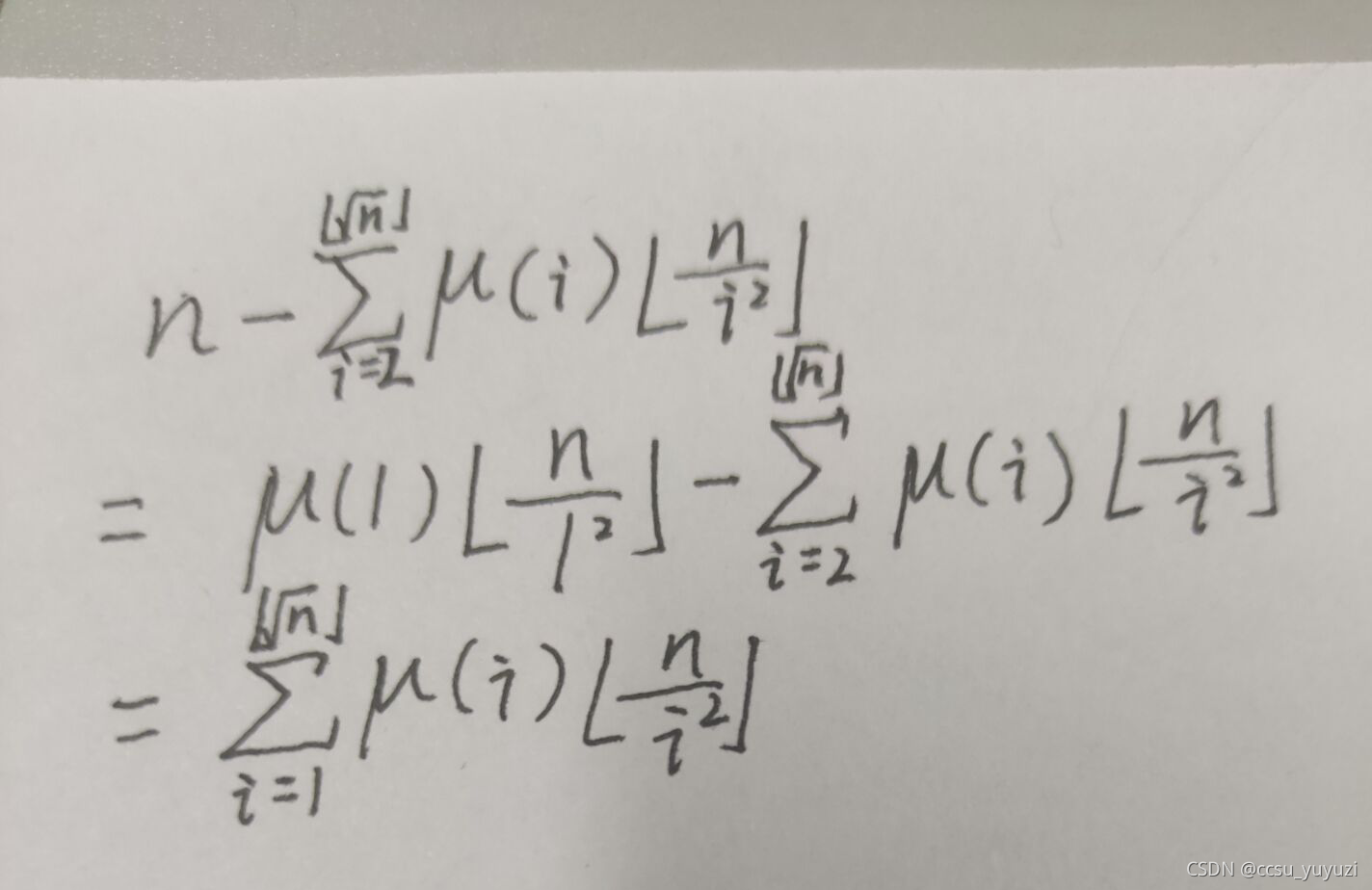
|
|
|
|
|
|
|
|
|
|
当求出来之后,我们就可以用二分来求此时的值:
|
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
#include<iostream>
|
|
|
|
|
#define ll long long
|
|
|
|
|
using namespace std;
|
|
|
|
|
int vis[40560],mo[40560],p[4253],n;
|
|
|
|
|
void init()
|
|
|
|
|
{
|
|
|
|
|
int tot=0,k;
|
|
|
|
|
mo[1]=1;
|
|
|
|
|
for(int i=2;i<=40559;i++)
|
|
|
|
|
{
|
|
|
|
|
if(vis[i]==0)
|
|
|
|
|
{
|
|
|
|
|
p[++tot]=i;
|
|
|
|
|
mo[i]=-1;
|
|
|
|
|
}
|
|
|
|
|
for(int j=1;j<=tot&&(k=i*p[j])<=40559;j++)
|
|
|
|
|
{
|
|
|
|
|
vis[k]=1;
|
|
|
|
|
if(i%p[j]!=0)mo[k]=-mo[i];
|
|
|
|
|
else
|
|
|
|
|
{
|
|
|
|
|
mo[k]=0;
|
|
|
|
|
break;
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
bool judge(int x)
|
|
|
|
|
{
|
|
|
|
|
ll ans=0;int i;
|
|
|
|
|
for(int i=1;i*i<=x;i++)
|
|
|
|
|
{
|
|
|
|
|
ans+=mo[i]*(x/(i*i));
|
|
|
|
|
}
|
|
|
|
|
if(ans>=n)return true;
|
|
|
|
|
else return false;
|
|
|
|
|
}
|
|
|
|
|
int main()
|
|
|
|
|
{
|
|
|
|
|
int t;
|
|
|
|
|
ll l,r,mid;
|
|
|
|
|
init();
|
|
|
|
|
scanf("%d",&t);
|
|
|
|
|
while(t--)
|
|
|
|
|
{
|
|
|
|
|
scanf("%d",&n);
|
|
|
|
|
l=n,r=1644934082;
|
|
|
|
|
while(l<r)
|
|
|
|
|
{
|
|
|
|
|
// cout<<l<<" oo "<<r<<endl;
|
|
|
|
|
mid=(l+r)>>1;
|
|
|
|
|
if(judge(mid))
|
|
|
|
|
r=mid;
|
|
|
|
|
else l=mid+1;
|
|
|
|
|
}
|
|
|
|
|
printf("%lld\n",r);
|
|
|
|
|
}
|
|
|
|
|
return 0;
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
例题:数字染色
|
|
|
|
|
题目意思:
|
|
|
|
|
|
|
|
|
|
给一个数组,在其中选数,看可以最多选出多少个gcd(最大公约数)>1的集合.
|
|
|
|
|
|
|
|
|
|
要求gcd>1,那我们就把他们的约数全部求出来,记录在一个si数组里(下标为这个约数的值,里面储存它作为约数被数组中的数用了多少次).然后我们遍历这个si数组,把每个约数可能组成的约数次数算出来,例如假设2作为约数被数组中的数被总共用了2次,那么它所有可以组成的约数就是1,2,4,也就是2^2-1种组合.而当我们选择计算了2的所有可以组成的公约数,3所有的可以组成的公约数,那么当我们计算6时,就会发现6已经被2和3计算过了,很好,容斥定理,用莫比乌斯函数作为系数求(2^n-1)的和,但是还有一个问题,当选择的是奇数个质数来计算个数时,应该加上,而莫比乌斯函数值为-1,而选偶数个时应该减去,所以在求莫比乌斯值时我们可以取个反,最终我们要求的式子就是:
|
|
|
|
|
|
|
|
|
|
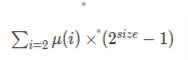
|
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
#include<iostream>
|
|
|
|
|
#define ll long long
|
|
|
|
|
using namespace std;
|
|
|
|
|
ll a[200005],vis[200005],p[200005],mo[200005];
|
|
|
|
|
ll si[200005];
|
|
|
|
|
const ll mod=1e9+7;
|
|
|
|
|
void init()
|
|
|
|
|
{
|
|
|
|
|
ll tot=0,k;
|
|
|
|
|
mo[1]=1;
|
|
|
|
|
for(int i=2;i<=200005;i++)
|
|
|
|
|
{
|
|
|
|
|
if(vis[i]==0)
|
|
|
|
|
{
|
|
|
|
|
p[++tot]=i;
|
|
|
|
|
mo[i]=1;
|
|
|
|
|
}
|
|
|
|
|
for(int j=1;j<=tot&&(k=i*p[j])<=200005;j++)
|
|
|
|
|
{
|
|
|
|
|
vis[k]=1;
|
|
|
|
|
if(i%p[j]==0)
|
|
|
|
|
{
|
|
|
|
|
mo[k]=0;
|
|
|
|
|
break;
|
|
|
|
|
}
|
|
|
|
|
else mo[k]=-mo[i];
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
ll qpow(ll pp,ll x)
|
|
|
|
|
{
|
|
|
|
|
ll ans=1;
|
|
|
|
|
while(x)
|
|
|
|
|
{
|
|
|
|
|
if(x&1)ans=ans%mod*pp%mod;
|
|
|
|
|
pp=pp*pp%mod;
|
|
|
|
|
x>>=1;
|
|
|
|
|
}
|
|
|
|
|
return ans;
|
|
|
|
|
}
|
|
|
|
|
int main()
|
|
|
|
|
{
|
|
|
|
|
ll n,ans=0;
|
|
|
|
|
init();
|
|
|
|
|
scanf("%lld",&n);
|
|
|
|
|
for(int i=1;i<=n;i++)
|
|
|
|
|
{
|
|
|
|
|
scanf("%lld",&a[i]);
|
|
|
|
|
for(int j=1;j*j<=a[i];j++)
|
|
|
|
|
{
|
|
|
|
|
if(j*j==a[i])
|
|
|
|
|
si[j]++;
|
|
|
|
|
else if(a[i]%j==0)
|
|
|
|
|
{
|
|
|
|
|
si[j]++;
|
|
|
|
|
si[a[i]/j]++;
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
for(int i=2;i<=200005;i++)
|
|
|
|
|
{
|
|
|
|
|
ans+=(mo[i]*(qpow(2,si[i])-1)%mod)%mod;
|
|
|
|
|
}
|
|
|
|
|
printf("%lld",(ans%mod+mod)%mod);
|
|
|
|
|
return 0;
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
ps:最后结果防止取模出负数要加上mod再取模.
|
|
|
|
|
|
|
|
|
|
之后会继续学习莫比乌斯反演的,如果本蒟蒻有什么错误望大佬指正.
|