diff --git a/TangDou/Topic/HuanGenDp/CF1187E_1.drawio b/TangDou/Topic/HuanGenDp/CF1187E_1.drawio
new file mode 100644
index 0000000..1808845
--- /dev/null
+++ b/TangDou/Topic/HuanGenDp/CF1187E_1.drawio
@@ -0,0 +1 @@
+7Vptc6M2EP41+tgOSIiXj2Dju+lcZzqTD+n1G2dkmxYjF8uxc7++KyHeLOKSHE6YaTOJB61Wu6tndx8QDiKL/eVTmRx2v/KU5Qhb6QWRJcLYdjBG8tdKnyuJT7RgW2apVmoFD9l3poWWlp6ylB17ioLzXGSHvnDNi4KtRU+WlCU/99U2PO97PSRbZgge1kluSh+zVOy01HaDduIzy7Y77drHXjWxT2plvZPjLkn5uSMiMSKLknNRXe0vC5ZL8GpcqnWrF2abwEpWiDEL/nh4XD3a6an8sov8X+Jl+vnw9081zEfxXO+45KciZXKRhUjES7HjW14k+RfODyC0QfgnE+JZ5yo5CQ6indjnepZdMvG7XP4z1aOvnZnlRVtWg+d6UIjyubNIDr9259plalSvO4qS/9VkRvowYdFIHfmpXLNbWOjySsotEzf0SKXH0l7laNA/Mb5nECEolCxPRPbUL6RE1+O20WtTBhc6a6/JoD2PDN4fd2deuFd2n5L81PfUSQSYAZ6CQXTeZYI9HBIFxBmosg94cjxU5LXJLjJx0YYXQqcHS4VNlucLnvNSGSYr+AmCW6g/sVKwy02c6llfc4BmaFcPzy3dUS3adYiulk0PLJ5HQb+Vkt7eCGRkI9B5NQL5P1+38+XOKl/EIC6z4e5IXJHthxMRl9UnLvvDmcv5r3aCM7ITvFl1gk3vkK+psf9XTP2pMdVLf+MZhNJ0G/Zor9uaE1ptoioSveoqM00Yb0+WY9CWed+ZjrYmoKeGZ+ZCT9RA0OSrWSF4BSD2PhhA1wDQJJBZAWg7dF4IegaC7rwRxNbMEPQNBL2ZIxjMDEHbbGMbxQTBMdiHC4qiJQoIigMlCVDsoMhHIQAW+wieXX2MYk9+RjDnosBDkYviFYoWyF8onRhFnjIUy1lQDmCVo5SXyCdyCkyDPgY97Oaw4+hbCVdbeYXHBIPvEQwxgyFjgnHuEYxtBuOMCYa+UzCmhI4Jj7xT4twxwbjvhJU3JhjvwxJ3/I4oFBddKlrEbrKXPFl8Ox6UujVOtOkbGfJBp/BBb/twp/Dh3vbhTeHDu+0DV9Pkh3y0RmQlwB8Bfhj2R6bwR8b7sytV74f8tUai1mf3GvAduMW8EFKmrIWqIyMU0kz3ZhTK3got1ZFNt1HoWRRYeiqwm0ZWjbhQrQ06jtSXzdrVCYd6vaIIbAa36cbWBOIif4nCeKDtwTbIQ1vaDiuOoNJboJQBnYC+jkdeDm1AIr2vlB3FWYHaa7RCQdDZvemii2usVjlymxpFxZqV5bAi0YUCj8q9wNZafqTSrL/SvsB461QxboBrDsY3nTYGm2Q2iWpcwJQK6bo4ZVig4esCCCOlGul9SlBclZvqjvAyuAMwOfJTXwQyhXqfsUK5MliH1Sta8K5SC5qAppaoCH0qa6KLIDSOBNeV4IJNadlVKLuyYmC2p2wpidMmO8RqyyoxEEC3sMKFyl9j2a0DazqlQePqoR4et0X/6b367rN+uVrwQj7xd9+3alGSZ9sChjnbSAvy0T1bJ3moxUK+2Ro8KfRfhnXOBrZfj3V8A19Gv/qg4Fwd9wPznOBZQweF6xdRI04KMGy/eK/eULX/vkDifwA=
\ No newline at end of file
diff --git a/TangDou/Topic/HuanGenDp/CF1187E_2.drawio b/TangDou/Topic/HuanGenDp/CF1187E_2.drawio
new file mode 100644
index 0000000..21784d6
--- /dev/null
+++ b/TangDou/Topic/HuanGenDp/CF1187E_2.drawio
@@ -0,0 +1 @@
+7Vptb9s2EP41/JhBFPX6UbLlFkMHbMuAtP3GWLSlVhZVio7t/vqREvXCyPFUVJoFbEEQ847HO95zx/OJCkCrw/kdw0XyG41JBkwjPgO0BqYJLdME8teILzXHQ4qxZ2mshDrGY/qdKKahuMc0JqUmyCnNeFrozC3Nc7LlGg8zRk+62I5mutUC78mA8bjF2ZD7lMY8UVzo+N3Ee5LuE2XaM9164oAbYeVJmeCYnnosFAG0YpTyenQ4r0gmwWtwqddt3phtN8ZIzscs+Pz4tHmC8ZF9SELv12gdvy++PTQwl/zSeMzoMY+JXGQAFFLGE7qnOc4+UFoIJhTML4Tzi4oVPnIqWAk/ZGqWnFP+US2X40+98frcJy6KKDmjX1t8YcXBjAcyfoLxnNHt14a5SbPWUB43IjnNSc1R81LtECEFWkmPbEtuwVLLkVhLDoXrO0IPhLOLEGAkwzx90XMFq5Tbt3Lt0t9pKrZiGs3xMO16yaVJekNXIRzeE65WdbEVg942OlYV8R+JPpwv+rAXfXgz+j8dphqlG3LW1OHUAvHDqNd6X3B21C31wiDUiAonU/qUpJw8FrgC4iSKrA43Lou67O3SswxbuKM5V8ExpcBOnIcVzSirFKON+PH9W6i/EMbJ+SZOatZ0DT19PUWfukppK1bSq5G2MRey5ozV7Bd7dEYLSNmlt0iSn/pz3bKK+vmTgEaeBHtZJwH9H6/b8XIWFS80qFzDAzdj5QqhF0xTudov2oteke5WuKz/6kGwRh4Ed1EHAdozxGtq7P8RU+/f6XKRpR+2lm5U1EkyW5drDarW8Gtnuqo1QXVCUH8sMP07lyd7gOCwXi0KQVvPuLZRvReAzgDAYQFZFIDQspeFoDtA0Fk2gq8fjizjzgh6AwTdZSOInPsh+MfLl2PygLh/8k4BNsq/Pv6Jrjy4g8gG4Rr4CEQWCEMQ2GY18kAYgMgBgQFCXw58F4QiYZ1M7DF8ZhrqzrejvAOsIHwoKwwDIQC94lwB2cyL0V59TqEGgggB8cTuwZ4XfsXxlRPBWrjjAdF1e2Lgyr99d6INCFfAW1UyEQjdSlEkZ4WwL1ZZlfAaeEhOCdVC3hRy03hgjvHAmsMDOJEHaIwH9pI9sMZ4AOfwwJrIA3uMB2gOD9BEHjhjPHCWnEXuGA/cJXuwLDXld2CLA2Kvq69r09hp5HQmbN1ERzr4IDuG/LksJvbK0U06M3jl6ibcGUygWidSJlBrQiakIJGo+hOag7V+S5mDr83JaorW/pQmzdqGq0x2ZNgmYz20uyHshJq9+XKf3mSn61W/KzpRrje29avI5tpRvVbs30QqFs7SfS7IjOykBtnVplucBYrN5aXP1SZavyfqtc3CS0Wr/b3VMF9pq99+EIZ6D33lMc5BV3po6/WbyBFNtCC7t9n15U33PwEo+hs=
\ No newline at end of file
diff --git a/TangDou/Topic/【换根】dfs专题.md b/TangDou/Topic/【换根】dfs专题.md
index 0e4ea2b..ebfb313 100644
--- a/TangDou/Topic/【换根】dfs专题.md
+++ b/TangDou/Topic/【换根】dfs专题.md
@@ -318,43 +318,6 @@ int main() {
}
```
-#### [$CF1187E$ $Tree$ $Painting$](https://www.luogu.com.cn/problem/CF1187E)
-**题意**
-给定一棵 $n$ 个点的树,初始全是白点
-
-要求你做 $n$ 步操作,每一次选定一个与一个黑点相隔一条边的白点,将它染成黑点,然后获得该白点被染色前所在的白色联通块大小的权值。
-
-第一次操作可以任意选点。
-
-求可获得的最大权值。
-
-**题解**
-分析一下题目性质,发现一旦选定初始点,不管我们之后扩展的顺序是怎样的,得到的权值都不会变(这个性质画画图很容易就可以发现)。
-
-现在问题又转变成选择一个初始点,最大化从它扩展到全树所得的价值,**经典二次扫描换根问题**。
-
-考虑每个结点,假设要扩展这个结点,可以得到多少权值,设这个值为 \(sum[x]\),另外,设以 \(x\) 为根的子树大小为 \(siz[x]\) 。
-
-那么很简单的,可以得到转移方程:
-
-\[sum[x]=\sum_{y\in Son(x)}siz[y]+siz[x] \]
-我们利用这个方程,求出任意一个结点为根时的 \(sum\) 值,然后进行换根,假设现在求出了 \(sum[1]\) 。
-
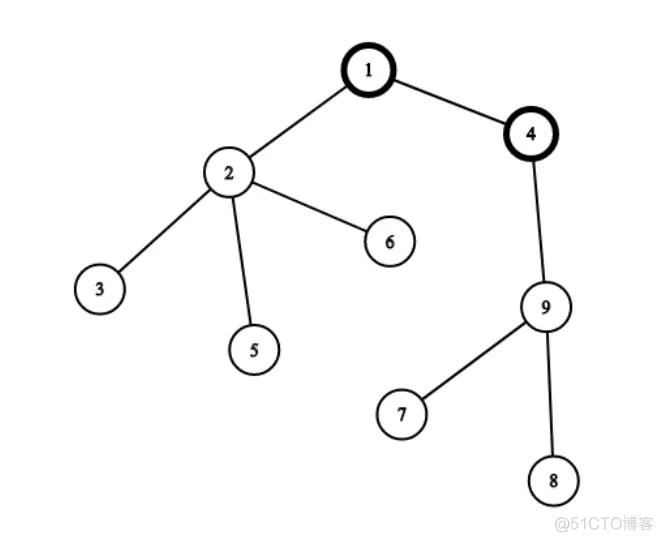
-请看下图
-
-
-
-假设我们现在把根从 1 换到 4 ,然后扩展,那么我们多得到的权值就是 {1,2,3,5,6} 这个连通块的价值,但是同样我们失去了 {4,9,7,8} 这个连通块的价值。
-
-因为我们是 dfs 进行转移,于是我们可以从父亲到儿子推出转移方程:
-
-\[sum[y]=sum[x]-sum[y]+n-sum[y],y\in Son(x) \]
-也就是说,我们从父亲转移到儿子的时候,得到了这个儿子子树大小的价值,损失了非该儿子子树的价值。
------------------------------------
-二次扫描与换根法
-
-
-
#### [$P2986$ 伟大的奶牛聚集](https://www.luogu.com.cn/problem/P2986)
**题目描述**
@@ -436,6 +399,186 @@ signed main() {
```
+#### [$CF1187E$ $Tree$ $Painting$](https://www.luogu.com.cn/problem/CF1187E)
+
+https://www.luogu.com.cn/blog/defKaeru/solution-cf1187e
+
+**题意**
+给定一棵有 $n$ 个结点的无根树,所有结点都是白色的。
+
+第一次操作可以 随意 使一个结点染成黑色,之后每次操作可以使一个与黑色结点相邻的白色结点变成黑色。
+
+**每次操作可以获得的权值为**: 被染成黑色的白色结点所在的白色连通块的结点数量。
+
+求可以获得的最大权值。
+
+**难点解析**
+
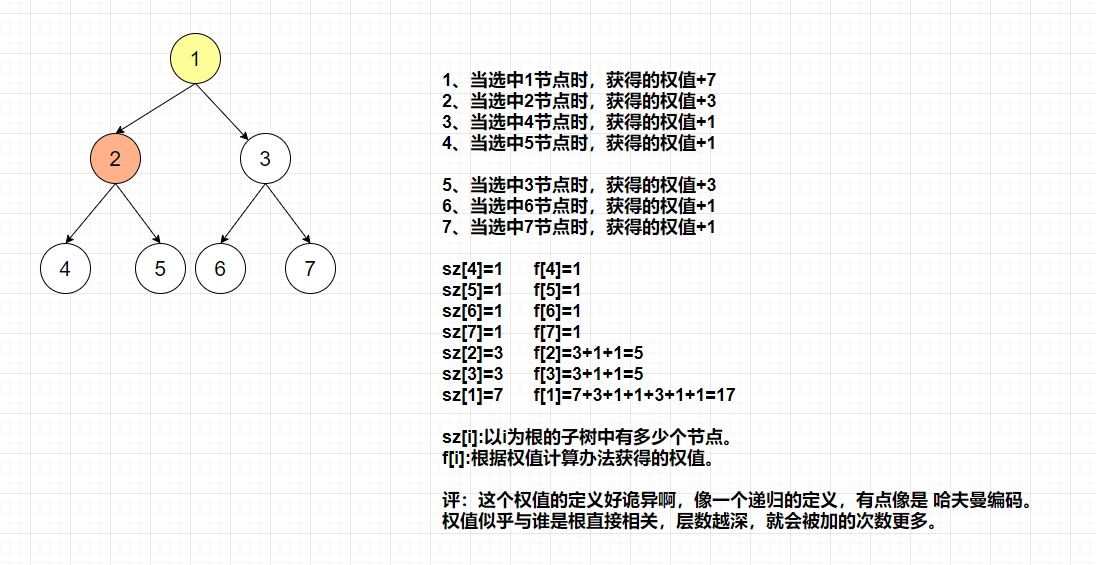
+最初时,我对这个**权值** 的认识不够深入,没有明白为什么根不同权值就会不同呢?后来仔细思考,发现是自己傻了,因为根不同,每个节点到根的距离就会不同,而权值的计算办法,其实是类似于哈夫曼树,父子隶属关系的不同最终的权值是不一样的,我们可以再画一下上面的图进行深入理解:
+
+
+
+
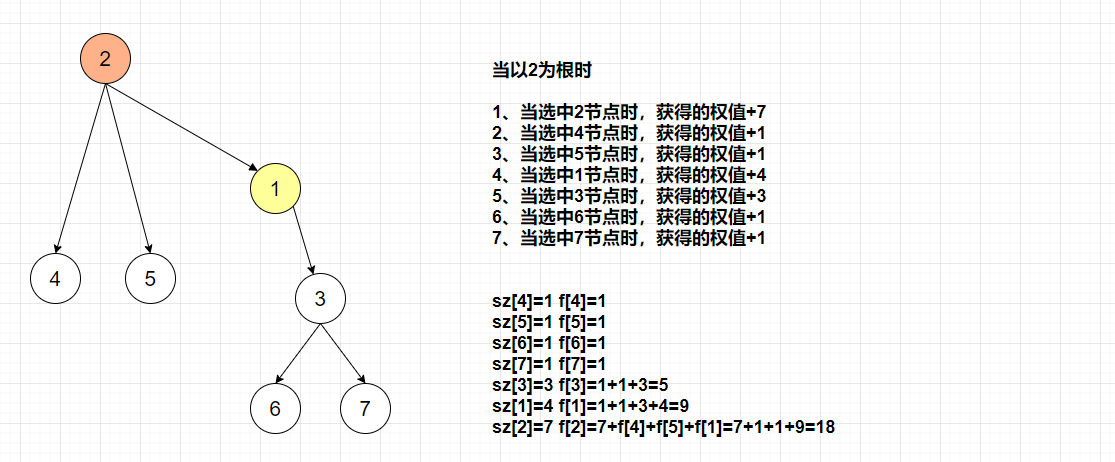
+
+
+
+**总结**:这个理解能力,目前看来有两种办法:
+- ① 多动手画图理解,尝试换根试一下。
+- ② 多做题,做的多了就一下明白它说什么了。
+
+
+**题解**
+不难发现只要选定了第一个被染色的结点,答案也就确定了, 也就是 选了谁是根最重要,其它的选择顺序不重要。
+
+所以有一个朴素做法就是以枚举每个结点为根,都做一次树形$dp$。
+
+以某一结点为根,记 $f_i$ 表示以 $i$ 为根的子树中,首先把 $i$ 染成黑色的答案。
+
+方程就是
+$\displaystyle \large f[u]=sz[u]+\sum_{v \in son[u]} f[v]$
+
+其中
+$sz[u]$ 表示以 $u$ 为根的子树大小,也就是染色时的白色连通块大小。
+
+**时间复杂度**
+$O(n^2)$ ,稳稳地暴毙,然后就会自然而然地想到换根$dp$。
+
+
+
+**换根$dp$**
+
+先考虑以任意一点为根,不妨记为 $1$ ,求出 $f$ 数组。
+
+然后记 $g[i]$ 表示以 $i$ 结点为根时的答案,尝试通过$1$号节点的计算已知值,进行换根,利用数学变换加快运算速度。
+
+显然,由于1号节点是根,它没有向上走的路径,所以它的向下所有获取的价值,就是总价值,也就是 $g[1] =f[1]$
+
+然后考虑 $g$ 数组从 **父亲到儿子** 的转移。
+
+
+
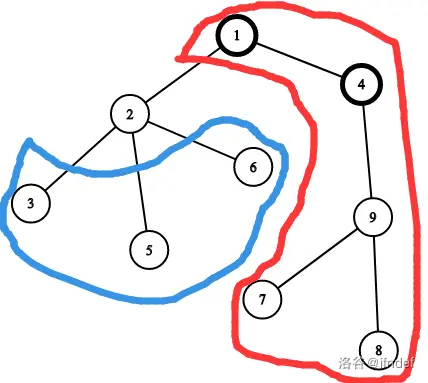
+以样例为例:
+
+
+
+我们假设当前以 $1$ 号为根,求出了 $f$ 数组,也就是知道了 $g[1]=f[1]$ ,然后要求出 $g[2]$ 。
+
+考虑一下答案的组成。
+
+首先考虑 $2$ 号结点的孩子的贡献,也就是图中蓝圈内的部分。这部分显然不会改变,贡献就是 $f[2] −sz[2]$ 。
+
+然后考虑父亲方向,也就是图中红圈部分对 $g[2]$ 的贡献。
+
+那么除了以 $2$ 号结点,与 $1$ 号结点相邻的其他子树都会对答案产生贡献,也就是说,我们只需要用以 $1$ 号结点为根时的权值减去以
+$2$ 为根的子树的贡献即可,也就是 $g[1]-f[2]-sz[2]$ 。
+
+不要忘了加上
+�
+n ,也就是初始的白色连通块大小。
+
+综合一下上述两种方向的贡献,可以得到:
+�
+2
+=
+(
+�
+2
+−
+�
+�
+�
+2
+)
++
+(
+�
+1
+−
+�
+2
+−
+�
+�
+�
+2
+)
++
+�
+=
+�
+1
++
+�
+−
+�
+�
+�
+2
+×
+2
+g
+2
+
+ =(f
+2
+
+ −siz
+2
+
+ )+(g
+1
+
+ −f
+2
+
+ −siz
+2
+
+ )+n=g
+1
+
+ +n−siz
+2
+
+ ×2 。
+
+推广到所有结点,就可以得到:
+
+�
+�
+=
+�
+�
+�
+�
+ℎ
+�
+�
+�
++
+�
+−
+�
+�
+�
+�
+×
+2
+g
+u
+
+ =g
+father
+u
+
+
+
+ +n−siz
+u
+
+ ×2
+然后跑两遍 dfs 就愉快的解决啦。
+
#### [$CF1324F$.$Maximum$ $White$ $Subtree$](https://www.luogu.com.cn/problem/CF1324F)
**题目大意**