'commit'

TangDou/AcWing_TiGao/T3/MiniPathYingYong/342.md

@@ -34,18 +34,18 @@
 **输出格式**
 第 $1..T$ 行：第 $i$ 行输出从 $S$ 到达城镇 $i$ 的最小花费，如果不存在，则输出 `NO PATH`。
 
-### 二、$Dijkstra$不能处理负权边，但可以处理负权初值
+### 二、$Dijkstra$不能处理负权边
 我们说了$Dijkstra$算法不能解决带有负权边的图，这是为什么呢？下面用一个例子讲解一下
 ![](https://img-blog.csdnimg.cn/51115e15bd3040d7a8b3980b523ed943.png)
 
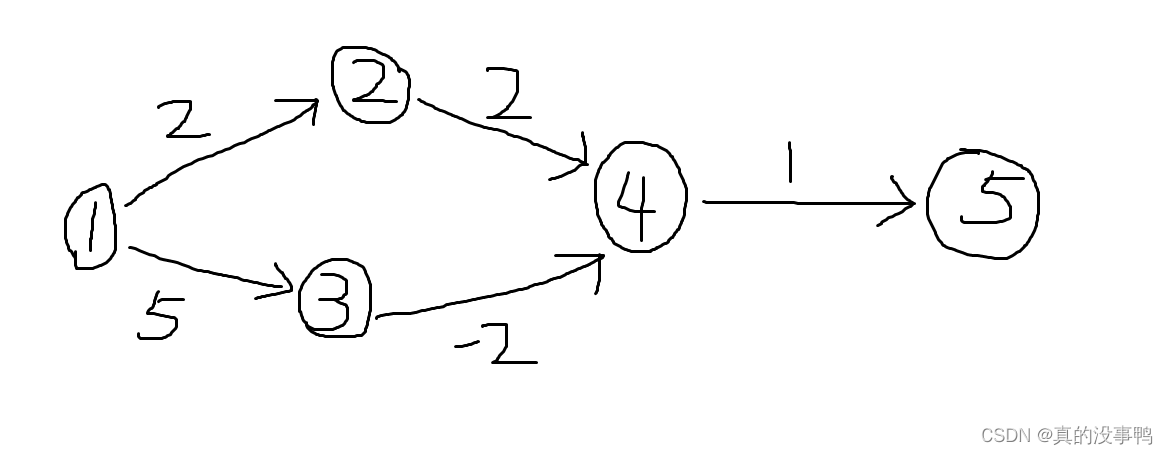
 以这里图为例，一共有五个点，也就说要循环$5$次，确定每个点的最短距离
 
 用$Dijkstra$算法解决的的详细步骤
-> 1. 初始$dist[1] = 0$，$1$号点距离起点$1$的距离为$0$
-> 2. 找到了未标识且离起点$1$最近的结点$1$，标记$1$号点，用$1$号点更新和它相连点的距离，$2$号点被更新成$dist[2] = 2$，$3$号点被更新成$dist[3] = 5$
-> 3. 找到了未标识且离起点$1$最近的结点$2$，标识$2$号点，用$2$号点更新和它相连点的距离，$4$号点被更新成$dist[4] = 4$
-> 4. 找到了未标识且离起点$1$最近的结点$4$，标识$4$号点，用$4$号点更新和它相连点的距离，$5$号点被更新成$dist[5] = 5$
-> 5. 找到了未标识且离起点$1$最近的结点$3$，标识$3$号点，用$3$号点更新和它相连点的距离，$4$号点被更新成$dist[4] = 3$
+> 1. 初始$dis[1] = 0$，$1$号点距离起点$1$的距离为$0$
+> 2. 找到了未标识且离起点$1$最近的结点$1$，标记$1$号点，用$1$号点更新和它相连点的距离，$2$号点被更新成$dis[2] = 2$，$3$号点被更新成$dis[3] = 5$
+> 3. 找到了未标识且离起点$1$最近的结点$2$，标识$2$号点，用$2$号点更新和它相连点的距离，$4$号点被更新成$dis[4] = 4$
+> 4. 找到了未标识且离起点$1$最近的结点$4$，标识$4$号点，用$4$号点更新和它相连点的距离，$5$号点被更新成$dis[5] = 5$
+> 5. 找到了未标识且离起点$1$最近的结点$3$，标识$3$号点，用$3$号点更新和它相连点的距离，$4$号点被更新成$dis[4] = 3$
 > 
 
 **结果**
@@ -56,10 +56,8 @@
 > 我们可以发现如果有负权边的话$4$号点经过标记后还可以继续更新
 但此时$4$号点已经被标记过了，所以$4$号点不能被更新了，只能一条路走到黑
 当用负权边更新$4$号点后$5$号点距离起点的距离我们可以发现可以进一步缩小成$4$。  
-所以总结下来就是:$dijkstra$**不能解决负权边** 是因为 $dijkstra$要求每个点被确定后，$dist[j]$就是最短距离了，之后就不能再被更新了（**一锤子买卖**），而如果有负权边的话，那已经确定的点的$dist[j]$不一定是最短了，可能还可以通过负权边进行更新。
+所以总结下来就是:$dijkstra$ **不能解决负权边** 是因为 $dijkstra$要求每个点被确定后，$dis[j]$就是最短距离了，之后就不能再被更新了（**一锤子买卖**），而如果有负权边的话，那已经确定的点的$dis[j]$不一定是最短了，可能还可以通过负权边进行更新。
 
-**负权初始值**
-那如果不是负权的边长，而是负权的初值呢？这个就没关系了，因为初值不影响算法逻辑，不信你看下有好多算法题都是判断$INF/2$,正无穷不也是在过程中松弛操作更改过吗，你是负的初始值也是没有问题，可以正确运行算法。
 
 ### 三、拓扑序+$Dijkstra$ + 缩点
 
@@ -99,7 +97,7 @@ int id[N];            // 节点在哪个连通块中
 vector<int> block[N]; // 连通块包含哪些节点
 int bcnt;             // 连通块序号计数器
 
-int dist[N];  // 最短距离(结果数组)
+int dis[N];  // 最短距离(结果数组)
 int in[N];    // 每个DAG(节点即连通块)的入度
 bool st[N];   // dijkstra用的是不是在队列中的数组
 queue<int> q; // 拓扑序用的队列
@@ -120,12 +118,12 @@ void dijkstra(int bid) {
     priority_queue<PII, vector<PII>, greater<PII>> pq;
     /*
     因为不确定连通块内的哪个点可以作为起点，所以就一股脑全加进来就行了，
-    反正很多点的dist都是inf（这些都是不能成为起点的）,那么可以作为起点的就自然出现在堆顶了
+    反正很多点的dis都是inf（这些都是不能成为起点的）,那么可以作为起点的就自然出现在堆顶了
 
     因为上面的写法把拓扑排序和dijkstra算法拼在一起了，如果不把所有点都加入堆，
     会导致后面其他块的din[]没有减去前驱边，从而某些块没有被拓扑排序遍历到。
     */
-    for (auto u : block[bid]) pq.push({dist[u], u});
+    for (auto u : block[bid]) pq.push({dis[u], u});
 
     while (pq.size()) {
         int u = pq.top().second;
@@ -136,10 +134,10 @@ void dijkstra(int bid) {
             int v = e[i];
             if (st[v]) continue;
 
-            if (dist[v] > dist[u] + w[i]) {
-                dist[v] = dist[u] + w[i];
+            if (dis[v] > dis[u] + w[i]) {
+                dis[v] = dis[u] + w[i];
                 // 如果是同团中的道路,需要再次进入Dijkstra的小顶堆，以便计算完整个团中的路径最小值
-                if (id[u] == id[v]) pq.push({dist[v], v});
+                if (id[u] == id[v]) pq.push({dis[v], v});
             }
             /*如果u和v不在同一个团中,说明遍历到的是航线
              此时，需要与拓扑序算法结合，尝试剪掉此边，是不是可以形成入度为的团
@@ -171,8 +169,8 @@ int main() {
     memset(h, -1, sizeof h);              // 初始化
     scanf("%d %d %d %d", &T, &R, &P, &S); // 城镇数量,道路数量,航线数量,出发点
 
-    memset(dist, 0x3f, sizeof dist); // 初始化最短距离
-    dist[S] = 0;                     // 出发点距离自己的长度是0,其它的最短距离目前是INF
+    memset(dis, 0x3f, sizeof dis); // 初始化最短距离
+    dis[S] = 0;                     // 出发点距离自己的长度是0,其它的最短距离目前是INF
 
     int a, b, c; // 起点，终点，权值
 
@@ -211,10 +209,10 @@ int main() {
 
     // 从S到达城镇i的最小花费
     for (int i = 1; i <= T; i++) {
-        if (dist[i] > INF / 2)
+        if (dis[i] > INF / 2)
             puts("NO PATH");
         else
-            cout << dist[i] << endl;
+            cout << dis[i] << endl;
     }
     return 0;
 }