From 512d96ab8d32cfd55b1696608e8c092f2e4cea73 Mon Sep 17 00:00:00 2001
From: =?UTF-8?q?=E9=BB=84=E6=B5=B7?= <10402852@qq.com>
Date: Tue, 12 Mar 2024 14:57:16 +0800
Subject: [PATCH] 'commit'
---
TangDou/AcWing/BeiBao/7.cpp | 2 +-
TangDou/AcWing/BeiBao/7.md | 17 +++----
TangDou/AcWing/BeiBao/背包问题专题.md | 55 +++++++++++++++++++++
3 files changed, 62 insertions(+), 12 deletions(-)
diff --git a/TangDou/AcWing/BeiBao/7.cpp b/TangDou/AcWing/BeiBao/7.cpp
index ce6e851..8dc29d0 100644
--- a/TangDou/AcWing/BeiBao/7.cpp
+++ b/TangDou/AcWing/BeiBao/7.cpp
@@ -9,7 +9,7 @@ int idx;
struct Node {
int v, w;
-} c[N * 12];
+} c[N * 31];
int main() {
cin >> n >> m;
diff --git a/TangDou/AcWing/BeiBao/7.md b/TangDou/AcWing/BeiBao/7.md
index e604331..1552fbb 100644
--- a/TangDou/AcWing/BeiBao/7.md
+++ b/TangDou/AcWing/BeiBao/7.md
@@ -49,19 +49,13 @@ $−1≤s_i≤1000$
该题就是一道 **混合背包** 的裸题
-* 将$01$背包看成是数量只有$1$个的多重背包问题。
-* 完全背包也不是真正的无限个数，因为受背包容量的限制，它最多可以使用的个数是$s_i=m/v_i$个,也就转化为多重背包问题。
-* 使用多重背包问题的二进制优化统一处理即可。
+* ① 将$01$背包看成是数量只有$1$个的多重背包问题
+* ② 完全背包也不是真正的无限个数，因为受背包容量的限制，它最多可以使用的个数是$s_i=m/v_i$个,也就转化为多重背包问题
-总结
-- $01$背包是多重背包的特殊形式；
+使用多重背包问题的二进制优化统一处理即可
-- 完全背包在背包容量限制下，也是多重背包的特殊形式
-- 之所以它们各自有各自的状态转移方程，是因为特殊形式时的状态转移方程更简单，但本质上符合多重背包状态转移方程。
-
-
-### 闫氏DP分析法
+### 闫氏$ DP$分析法
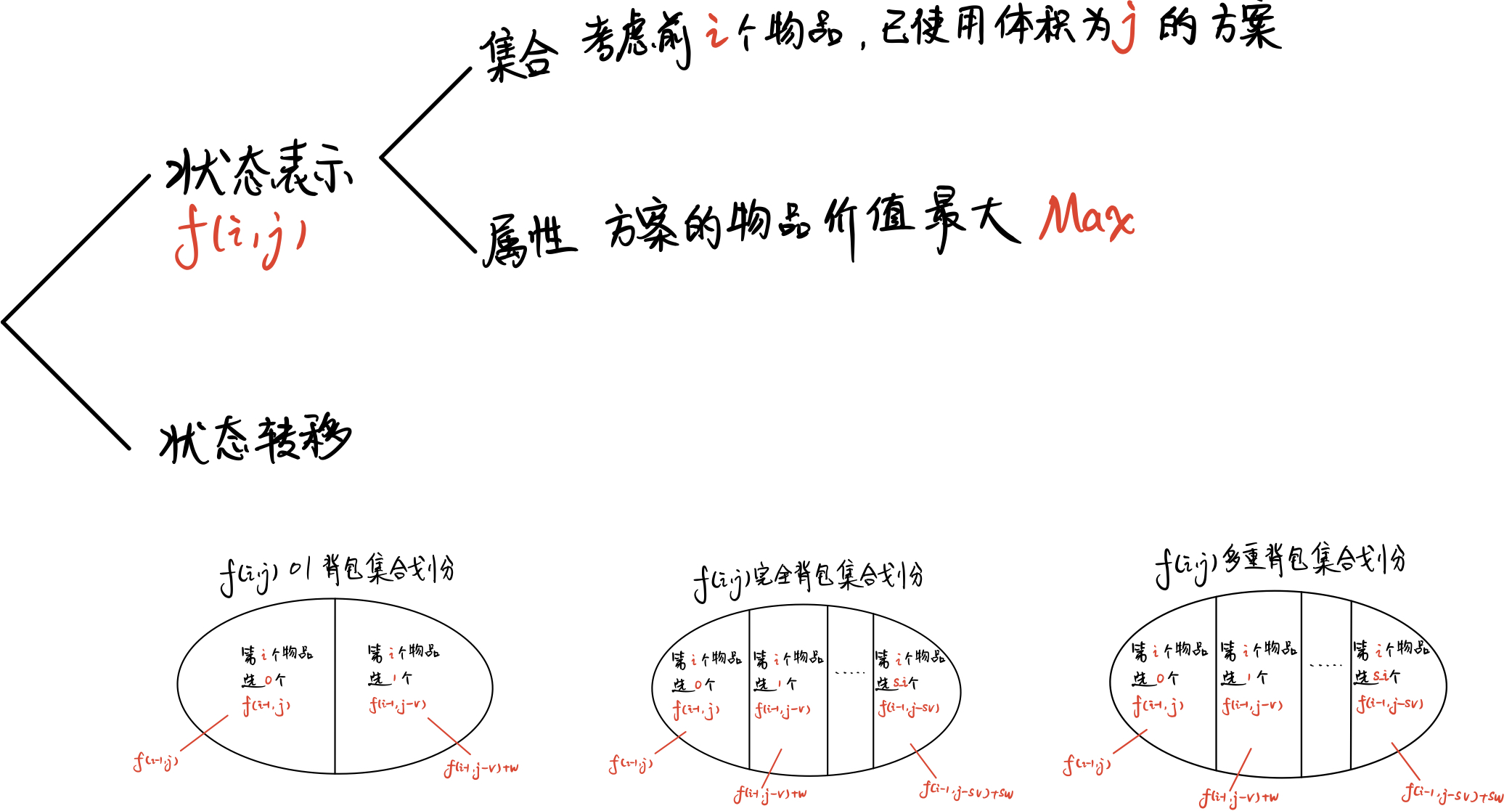### 一维数组解法 【推荐】
@@ -77,7 +71,7 @@ int idx;
struct Node {
int v, w;
-} c[N * 12];
+} c[N * 31];
int main() {
cin >> n >> m;
@@ -111,4 +105,5 @@ int main() {
printf("%d\n", f[m]);
return 0;
}
+
```
diff --git a/TangDou/AcWing/BeiBao/背包问题专题.md b/TangDou/AcWing/BeiBao/背包问题专题.md
index 4c41413..9469a89 100644
--- a/TangDou/AcWing/BeiBao/背包问题专题.md
+++ b/TangDou/AcWing/BeiBao/背包问题专题.md
@@ -497,4 +497,59 @@ int main() {
return 0;
}
+```
+### 七、混合背包
+
+* ① 将$01$背包看成是数量只有$1$个的多重背包问题
+* ② 完全背包也不是真正的无限个数，因为受背包容量的限制，它最多可以使用的个数是$s_i=m/v_i$个,也就转化为多重背包问题
+
+使用多重背包问题的二进制优化统一处理即可
+
+```cpp {.line-numbers}
+#include
+
+using namespace std;
+const int N = 1e5 + 10;
+int n; // 物品种类
+int m; // 背包容量
+int f[N]; // dp数组
+int idx;
+
+struct Node {
+ int v, w;
+} c[N * 31];
+
+int main() {
+ cin >> n >> m;
+
+ // 二进制打包
+ for (int i = 1; i <= n; i++) {
+ // 体积，价值，个数
+ int v, w, s;
+ cin >> v >> w >> s;
+
+ // 根据题意做一些小的变形
+ if (s == -1)
+ s = 1; // 题目中s=-1表示只有1个
+ else if (s == 0)
+ s = m / v; // 完全背包(其实本质上就是多重背包):最多总体积/该物品体积向下取整
+ // 如果是其它大于0的数字，那么是多重背包
+
+ // 将完全背包和多重背包利用二进制优化转化为01背包
+ for (int j = 1; j <= s; j *= 2) {
+ c[++idx] = {j * v, j * w};
+ s -= j;
+ }
+ // 不够下一个2^n时，独立成包
+ if (s) c[++idx] = {s * v, s * w};
+ }
+ // 01背包
+ for (int i = 1; i <= idx; i++)
+ for (int j = m; j >= c[i].v; j--)
+ f[j] = max(f[j], f[j - c[i].v] + c[i].w);
+ // 输出
+ printf("%d\n", f[m]);
+ return 0;
+}
+
```
\ No newline at end of file