|
|
|
|
@ -46,52 +46,93 @@ $1≤n≤100 ,0≤k≤200,1≤f(i,j)≤1000$
|
|
|
|
|
|
|
|
|
|
$kruskal$算法是 **求连通块** 的,所以这个题直接用 $kruskal$ 很容易求出来。
|
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
if (cnt < n - 1) res = INF;
|
|
|
|
|
```
|
|
|
|
|
这句话需要注释掉,比如下面的数据用例:
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
6 6
|
|
|
|
|
1 2 5
|
|
|
|
|
1 3 4
|
|
|
|
|
2 3 8
|
|
|
|
|
4 5 7
|
|
|
|
|
4 6 2
|
|
|
|
|
5 6 1
|
|
|
|
|
```
|
|
|
|
|
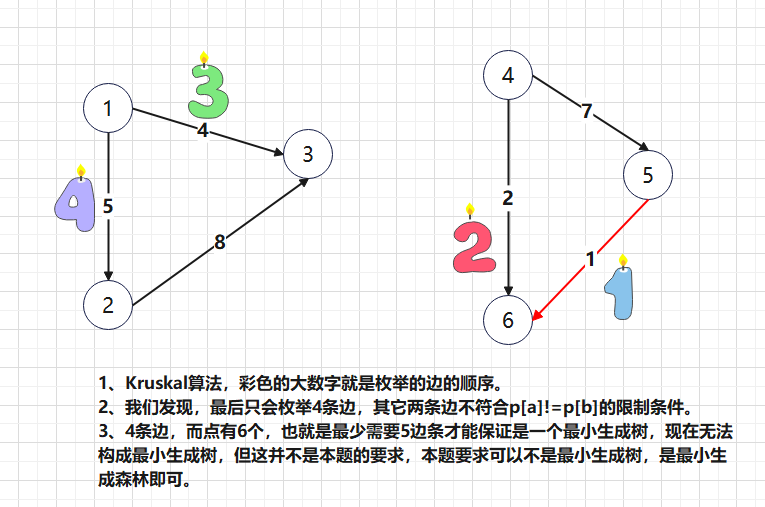
我们发现,$1,2,3$是一伙,$4,5,6$是另一伙,这两个家庭不通!如果按照模板的意思,那么就没有最小生成树!
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
using namespace std;
|
|
|
|
|
const int N = 110, M = 210;
|
|
|
|
|
int n, m, fa[N];
|
|
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
|
|
|
|
|
|
|
//结构体
|
|
|
|
|
struct Edge {
|
|
|
|
|
int a, b, w;
|
|
|
|
|
bool operator<(const Edge &t) {
|
|
|
|
|
return w < t.w;
|
|
|
|
|
int n, m; // n条顶点,m条边
|
|
|
|
|
int res; // 最小生成树的权值和
|
|
|
|
|
int cnt; // 最小生成树的结点数
|
|
|
|
|
|
|
|
|
|
// Kruskal用到的结构体
|
|
|
|
|
struct Node {
|
|
|
|
|
int a, b, c;
|
|
|
|
|
bool const operator<(const Node &t) const {
|
|
|
|
|
return c < t.c; // 边权小的在前
|
|
|
|
|
}
|
|
|
|
|
} e[M];
|
|
|
|
|
} edge[M]; // 数组长度为是边数
|
|
|
|
|
|
|
|
|
|
//并查集
|
|
|
|
|
// 并查集
|
|
|
|
|
int p[N];
|
|
|
|
|
int find(int x) {
|
|
|
|
|
if (fa[x] != x) fa[x] = find(fa[x]); //路径压缩
|
|
|
|
|
return fa[x];
|
|
|
|
|
if (p[x] != x) p[x] = find(p[x]);
|
|
|
|
|
return p[x];
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
// Kruskal算法
|
|
|
|
|
void kruskal() {
|
|
|
|
|
// 1、按边权由小到大排序
|
|
|
|
|
sort(edge, edge + m);
|
|
|
|
|
// 2、并查集初始化
|
|
|
|
|
for (int i = 1; i <= n; i++) p[i] = i;
|
|
|
|
|
// 3、迭代m次
|
|
|
|
|
for (int i = 0; i < m; i++) {
|
|
|
|
|
int a = edge[i].a, b = edge[i].b, c = edge[i].c;
|
|
|
|
|
a = find(a), b = find(b);
|
|
|
|
|
if (a != b)
|
|
|
|
|
p[a] = b, res += c, cnt++; // cnt是指已经连接上边的数量
|
|
|
|
|
}
|
|
|
|
|
// 这句话需要注释掉,原因如下:
|
|
|
|
|
/*
|
|
|
|
|
6 6
|
|
|
|
|
1 2 5
|
|
|
|
|
1 3 4
|
|
|
|
|
2 3 8
|
|
|
|
|
4 5 7
|
|
|
|
|
4 6 2
|
|
|
|
|
5 6 1
|
|
|
|
|
我们发现,1,2,3是一伙,4,5,6是另一伙,这两个家庭不通!如果按照模板的意思,那么就没有最小生成树!
|
|
|
|
|
这么说是没有问题的,但本题不是求最小生成树,而是求最小生成森林!所以,下面的特判需要注释掉!
|
|
|
|
|
*/
|
|
|
|
|
// 4、特判是不是不连通
|
|
|
|
|
// if (cnt < n - 1) res = INF;
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
int main() {
|
|
|
|
|
cin >> n >> m;
|
|
|
|
|
|
|
|
|
|
//并查集初始化
|
|
|
|
|
for (int i = 1; i <= n; i++) fa[i] = i;
|
|
|
|
|
|
|
|
|
|
int sum = 0;
|
|
|
|
|
// Kruskal算法直接记录结构体
|
|
|
|
|
for (int i = 0; i < m; i++) {
|
|
|
|
|
int a, b, c;
|
|
|
|
|
cin >> a >> b >> c;
|
|
|
|
|
e[i] = {a, b, c};
|
|
|
|
|
edge[i] = {a, b, c};
|
|
|
|
|
sum += c;
|
|
|
|
|
}
|
|
|
|
|
sort(e, e + m); //不要忘记e数组的长度是边的数量
|
|
|
|
|
|
|
|
|
|
int res = 0;
|
|
|
|
|
//枚举每条边
|
|
|
|
|
for (int i = 0; i < m; i++) {
|
|
|
|
|
int a = find(e[i].a), b = find(e[i].b), c = e[i].w;
|
|
|
|
|
if (a != b)
|
|
|
|
|
fa[a] = b;
|
|
|
|
|
else
|
|
|
|
|
res += c; //去掉的边权
|
|
|
|
|
}
|
|
|
|
|
printf("%d\n", res);
|
|
|
|
|
kruskal();
|
|
|
|
|
printf("%d\n", sum - res);
|
|
|
|
|
return 0;
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
### 三、$Prim$算法
|
|
|
|
|
@ -103,39 +144,46 @@ using namespace std;
|
|
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
|
|
|
|
|
|
|
const int N = 110;
|
|
|
|
|
int w[N][N];
|
|
|
|
|
int dist[N];
|
|
|
|
|
bool st[N];
|
|
|
|
|
int n, m, sum;
|
|
|
|
|
int b[N];//桶,记录哪些点已经处理过了,找出未处理过的进行一下Flood Fill
|
|
|
|
|
|
|
|
|
|
int prim(int source) {
|
|
|
|
|
memset(dist, 0x3f, sizeof dist);
|
|
|
|
|
dist[source] = 0;
|
|
|
|
|
b[source] = 1;
|
|
|
|
|
|
|
|
|
|
int res = 0;
|
|
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
|
|
|
|
|
|
|
int b[N];
|
|
|
|
|
|
|
|
|
|
int n, m;
|
|
|
|
|
int g[N][N]; // 稠密图,邻接矩阵
|
|
|
|
|
int dis[N]; // 这个点到集合的距离
|
|
|
|
|
bool st[N]; // 是不是已经使用过
|
|
|
|
|
int res; // 最小生成树里面边的长度之和
|
|
|
|
|
int sum; // 总边长
|
|
|
|
|
// 普利姆算法求最小生成树
|
|
|
|
|
int prim(int s) {
|
|
|
|
|
// 由于调用多次prim,所以每次需要清零
|
|
|
|
|
memset(dis, 0x3f, sizeof dis);
|
|
|
|
|
res = 0;
|
|
|
|
|
// 标识
|
|
|
|
|
b[s] = 1;
|
|
|
|
|
|
|
|
|
|
for (int i = 0; i < n; i++) { // 迭代n次
|
|
|
|
|
int t = -1;
|
|
|
|
|
for (int j = 1; j <= n; j++)
|
|
|
|
|
if (!st[j] && (t == -1 || dist[t] > dist[j]))
|
|
|
|
|
t = j;
|
|
|
|
|
st[t] = true;
|
|
|
|
|
if (!st[j] && (t == -1 || dis[t] > dis[j])) t = j;
|
|
|
|
|
|
|
|
|
|
if (dist[t] != INF) res += dist[t], b[t] = 1;
|
|
|
|
|
// if (i && dis[t] == INF) return INF; // 非连通图,没有最小生成树
|
|
|
|
|
if (i && dis[t] != INF) res += dis[t], b[t] = 1;
|
|
|
|
|
for (int j = 1; j <= n; j++)
|
|
|
|
|
dist[j] = min(dist[j], w[t][j]);
|
|
|
|
|
if (!st[j] && g[t][j] < dis[j]) dis[j] = g[t][j];
|
|
|
|
|
|
|
|
|
|
st[t] = true;
|
|
|
|
|
}
|
|
|
|
|
return res;
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
int main() {
|
|
|
|
|
cin >> n >> m;
|
|
|
|
|
memset(w, 0x3f, sizeof w);
|
|
|
|
|
memset(g, 0x3f, sizeof g);
|
|
|
|
|
|
|
|
|
|
while (m--) {
|
|
|
|
|
int a, b, c;
|
|
|
|
|
cin >> a >> b >> c;
|
|
|
|
|
w[a][b] = w[b][a] = c;
|
|
|
|
|
g[a][b] = g[b][a] = c;
|
|
|
|
|
sum += c; // 总边长
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
@ -146,4 +194,5 @@ int main() {
|
|
|
|
|
printf("%d\n", sum - s);
|
|
|
|
|
return 0;
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
```
|
|
|
|
|
|