diff --git a/TangDou/AcWing_TiGao/T5/QiWang/217_dfs.cpp b/TangDou/AcWing_TiGao/T5/QiWang/217.cpp similarity index 88% rename from TangDou/AcWing_TiGao/T5/QiWang/217_dfs.cpp rename to TangDou/AcWing_TiGao/T5/QiWang/217.cpp index 9e6bbba..1fc317c 100644 --- a/TangDou/AcWing_TiGao/T5/QiWang/217_dfs.cpp +++ b/TangDou/AcWing_TiGao/T5/QiWang/217.cpp @@ -16,7 +16,7 @@ double dfs(int u) { f[u] = 0; // 初始化为0，准备开始填充 for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; - f[u] += (w[i] + dfs(j)) / out[u]; // 看推的公式 + f[u] += (w[i] + dfs(j)) / out[u]; } return f[u]; } diff --git a/TangDou/AcWing_TiGao/T5/QiWang/217.drawio b/TangDou/AcWing_TiGao/T5/QiWang/217.drawio deleted file mode 100644 index d9a22c8..0000000 --- a/TangDou/AcWing_TiGao/T5/QiWang/217.drawio +++ /dev/null @@ -1 +0,0 @@ -5VpLc9owEP41zLSHMtbLj2NDHj00M+mkbdLePFiAEmNRI4rJr6+MZbAlB0gCVgkzHLwraWV9+3m1WtFBvXF2lYaT0TWPaNyBTpR10HkHQoAh7OQ/J1oUGt8jhWKYskh1Witu2RNVSkdpZyyi01pHwXks2KSu7PMkoX1R04Vpyuf1bgMe12edhENqKG77YWxq71gkRkrrErxu+ELZcFRODdygaBmHZW+1lOkojPi8okIXHdRLORfF0zjr0ThHrwSmGHf5TOvqzVKaiF0GDB7cy3F2+fPp4QpP/izI7Ovi/pOy8jeMZ2rFD+ptxaLEQJqRcEvhbD5igt5Own7eMpcel7qRGMdSAvIxnE4KHwxYRuWsZ1OR8scVcFhqBjwRyssQlbKaqmFF5evRVNCsolIrvKJ8TEW6kF1Ua4AV2opvIFDyfO09olSjit9KXaj4MlxZXiMqHxSozQBf9JxfT78ZFL9/XH0PxfUw/PatAeAM2EbYgLMB9GcRdoM6wtCxjDA0EUZHjbDneTWEEbKMMDIRhkeNcKBxGNvmMDYRfjxqhH2/jjCxzWFiIJwcNcAu1AC2TWHXANjEN4k+5zmZlPpxOJ2yfh3WlM+SKMfz3NEQ9KRMMybuVVv+/Ct/7hIlnWeVpvNFKSRyaffK/FKojMrF9bClVI4z/VkshkZGumgkK1M+S/t0e84lwnRIxbbUwSTAjg5OaRwK9rf+uk1eVzPccCYXst6EHC1EehpximWqUdW0UzdENENQM1TgYBhaknC17Nfz0jN4edeQgckPUdTJWFCgx2OeSk3CkzwuDFgca6owZsMkZ7TkAZX6s/yzZvIE8Vk1jFkUxc8Flc2U30cg1uIE8M044TbQCB0qTvitxYku9CuhArwmULw4TORGb2jKJFY5GZa9LIQOaDN0BNoXLw3vJ3RApBk6cOgI2qMq2Zmp/8XWhK3yy8V1Wug5za788n3YdT3PdQMijWpWEfa6aHn4klsfQq7jtsq9sgB2ePKBN1BvFTYrKdUugdMCZZFVypZlz7dSNgBBTlnfgW7g5QyumSXY6WIMCCI+CggO2mWsWeo6VLh8wQlgA2e1MwHcwtmltJ+9fVOVZSuRiVUiBxtCpsztq40owK8jOXBg/XPBoN0zAzBrinum8u603HZU3SMD8TEwEDj6yVTPCnelmavXqFo+mQKzrnqogPmC/PK1W/q+8tJNtyj/NzNPIy81S9Ut7PJvyEs9WI+nEi+7+zw8Bi6/oyhrVv7vGi4IT6YACD3LBUBg3hTcNdwnvluHGJ8Wari6adcjTTVy8/7x3XrE9zSHNPxppF2HmEXywYcMfDwdl7hAcwm27RKzGCxdgk7IJZ7216rVRZ4tl5Tz110CT8gl+t6Obe/t0KwBSpc8npBL9DsrQg7mEimu/z1apMvrP+Gii38= \ No newline at end of file diff --git a/TangDou/AcWing_TiGao/T5/QiWang/217.md b/TangDou/AcWing_TiGao/T5/QiWang/217.md index 367017c..364cf5e 100644 --- a/TangDou/AcWing_TiGao/T5/QiWang/217.md +++ b/TangDou/AcWing_TiGao/T5/QiWang/217.md @@ -72,22 +72,26 @@ $f(i)$：从$i$跳到$N$的期望长度。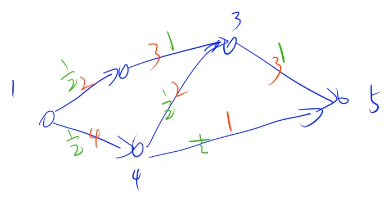边界$f(N)=0$ ![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312191619342.png) -事件发生的期望的线性性 $$\large E(aX+bY)=aE(X)+bE(Y)$$ +题意:给定一个$DAG$，求路径和。 -$f[i]$: 从 $i$ 跳到 $N$ 的期望长度 -边界: $f[N]=0$ -答案: $f[1]$ +由题意知，题目中的$K$就是每个点的出度。 -![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312191621193.png) +然后，又由题意知，最后一个点，它没有出度，而到自己的距离为$0$，即状态已经确定。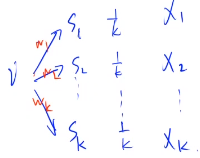 -则有如下递推式： +用前向星存图，从第一个点开始 -$\large f(i)=E(\frac{1}{k}(w_1+x_1)+\frac{1}{k}(w_2+x_2)+⋯+\frac{1}{k}(w_k+x_k)) \\ -=E(\frac{1}{k}(w_1+x_1))+E(\frac{1}{k}(w_2+x_2))+⋯+E(\frac{1}{k}(w_k+x_k))\\ -=\frac{1}{k}((w_1+E(x_1))+(w_2+E(x_2))+⋯+(w_k+E(x_k))) \\ -=\frac{1}{k}((w_1+f(i_1))+(w_2+f(i_2))+⋯+(w_k+f(i_k)))$ +$DFS$,每次枚举它所连的边，并把边的边权 ($w[i]$)加上，最后除以它的出度即可。 +方程： +$dp[n]=0 \\ +dp[i]+=(dp[son[i]]+e[son[i]].val)/out[i]$ + +其中， + +$son[i]$是$i$所连得边，$e$是前向星，$val$是边权,$out[i]$是$i$的出度。 + +#### $Code$ ```cpp {.line-numbers} #include using namespace std; @@ -107,7 +111,7 @@ double dfs(int u) { f[u] = 0; // 初始化为0，准备开始填充 for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; - f[u] += (w[i] + dfs(j)) / out[u]; // 看推的公式 + f[u] += (w[i] + dfs(j)) / out[u]; } return f[u]; } diff --git a/TangDou/AcWing_TiGao/T5/QiWang/217_DaoTui.cpp b/TangDou/AcWing_TiGao/T5/QiWang/217_DaoTui.cpp deleted file mode 100644 index c3378c1..0000000 --- a/TangDou/AcWing_TiGao/T5/QiWang/217_DaoTui.cpp +++ /dev/null @@ -1,43 +0,0 @@ -#include -using namespace std; -const int N = 100010, M = N << 1; -int n, m; -int in[N], g[N]; // 入度，入度的备份数组，原因：in在topsort中会不断变小受破坏 -double f[N]; - -// 链式前向星 -int e[M], h[N], idx, w[M], ne[M]; -void add(int a, int b, int c = 0) { - e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++; -} - -void topsort() { - queue q; - q.push(n); - f[n] = 0; // n到n的距离期望是0 - while (q.size()) { - int u = q.front(); - q.pop(); - for (int i = h[u]; ~i; i = ne[i]) { // 枚举每条入边(因为是反向图) - int v = e[i]; - f[v] += (f[u] + w[i]) / g[v]; - in[v]--; - if (in[v] == 0) q.push(v); - } - } -} -int main() { - memset(h, -1, sizeof h); - cin >> n >> m; - - while (m--) { - int a, b, c; - cin >> a >> b >> c; - add(b, a, c); // 反向图,计算从n到1 - in[a]++; // 入度 - g[a] = in[a]; // 入度数量 - } - topsort(); - printf("%.2lf\n", f[1]); - return 0; -} \ No newline at end of file diff --git a/TangDou/AcWing_TiGao/T5/QiWang/217_ZhengTui.cpp b/TangDou/AcWing_TiGao/T5/QiWang/217_ZhengTui.cpp deleted file mode 100644 index c843c08..0000000 --- a/TangDou/AcWing_TiGao/T5/QiWang/217_ZhengTui.cpp +++ /dev/null @@ -1,59 +0,0 @@ -#include -using namespace std; -const int N = 1e5 + 10, M = N << 1; - -// 邻接表 -int h[N], e[M], ne[M], w[M], idx; -void add(int a, int b, int c) { - e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++; -} - -int n, m; // n个顶点，m条边 - -int out[N], in[N]; // 出度,入度 -double f[N], g[N]; // f:数学期望结果 g:概率 - -void topsort() { - queue q; - // 起点为1,起点的概率为100% - q.push(1); - g[1] = 1.0; - f[1] = 0.0; - - // DAG，执行拓扑序,以保证计算的顺序正确，确保递归过程中，前序数据都已处理完毕 - while (q.size()) { - auto u = q.front(); - q.pop(); - - for (int i = h[u]; ~i; i = ne[i]) { // 枚举的是每边相邻边 - int v = e[i]; // 此边，一端是t，另一端是j - // 此边边条w[i] - f[v] += (f[u] + w[i] * g[u]) / out[u]; - g[v] += g[u] / out[u]; // g[j]也需要概率累加 - // 拓扑序的标准套路 - in[v]--; - if (!in[v]) q.push(v); - } - } -} - -int main() { - // 初始化邻接表 - memset(h, -1, sizeof h); - cin >> n >> m; - - while (m--) { - int a, b, c; - cin >> a >> b >> c; - add(a, b, c); - // 维护出度，入度 - out[a]++, in[b]++; - } - // 拓扑序 - topsort(); - - // 正向递推，输出结果，保留两位小数 - printf("%.2lf", f[n]); - - return 0; -} \ No newline at end of file