|
|
|
|
@ -57,22 +57,24 @@ $id[1]=8$ 表示第$1$个亲戚家住在$8$号车站附近,记录每个亲戚与
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 2、思考过程
|
|
|
|
|
① 必须由佳佳的家出发,也就出发点肯定是$1$号车站
|
|
|
|
|
② 现在想求佳佳去$5$个亲戚家,每一家都需要走到,不能漏掉任何一家,但顺序可以任意。这里要要用一个关系数组$id[]$来把亲戚家的编号与车站号挂接一下。
|
|
|
|
|
③ 看到是最短路径问题,而且权值是正整数,考虑唯一可能性就是$Dijkstra$。
|
|
|
|
|
① 必须由佳佳的家出发,也就是出发点肯定是$1$号车站
|
|
|
|
|
② 现在想求佳佳去$5$个亲戚家,每一家都需要走到,不能漏掉任何一家,但顺序可以任意。这里要用一个关系数组$id[]$来把亲戚家的编号与车站号挂接一下。
|
|
|
|
|
③ 看到是最短路径问题,而且权值是正整数,考虑$Dijkstra$。
|
|
|
|
|
④ 但$Dijkstra$只能是单源最短路径求解,比如佳佳去二姨家,最短路径是多少。佳佳去三舅家,最短路径是多少。本题不是问某一家,问的是佳佳全去到,总的路径和最短是多少,这样的话,直接使用$Dijkstra$就无效了。
|
|
|
|
|
⑤ 继续思考:因为亲戚家只有$5$个,可以从这里下手,通过全排列的办法,枚举出所有的可能顺序,此时,计算次数=$5*4*3*2*1=120$次。 就算是跑个$120$次的$Dijkstra$也不是啥大问题,就是常数大一点呗,可以试试。
|
|
|
|
|
⑤ 继续思考:因为亲戚家只有$5$个,可以从这里下手,通过全排列的办法,枚举出所有的可能顺序,此时,计算次数=$5*4*3*2*1=120$次。
|
|
|
|
|
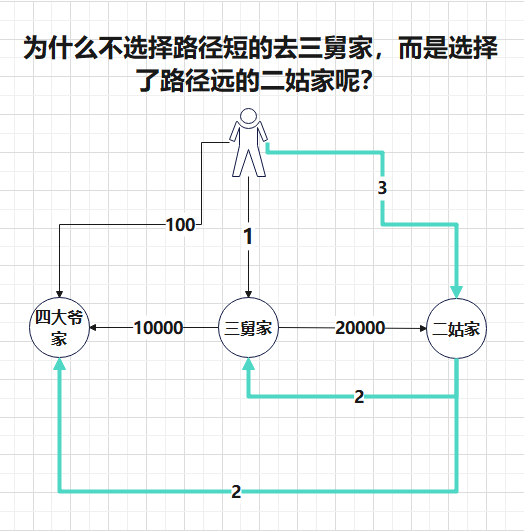
⑥ 跑多次$Dijkstra$是在干什么呢?就是在分别以二姨,三舅,四大爷家为出发点,分别计算出到其它亲戚家的最短距离,如果我们把顺序分别枚举出来,每次查一下已经预处理出来的两个亲戚家的最短距离,再加在一起,不就是可以进行$PK$最小值了吗?
|
|
|
|
|
|
|
|
|
|
至此,整体思路完成。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 3.编码步骤
|
|
|
|
|
|
|
|
|
|
* **$6$次最短路**
|
|
|
|
|
分别以佳佳家、五个亲戚家为出发点($id[i]~ i\in[0,5]$),求$6$次最短路,相当于打表,一会要查
|
|
|
|
|
|
|
|
|
|
* **求全排列**
|
|
|
|
|
因为佳佳所有的亲戚都要拜访到,现在不知道的是什么样顺序拜访才是时间最少的。 把所有可能顺序都 **枚举** 出来,通过查表,找出两个亲戚家之间的最小时间,累加结果的和,再$PJ$最小就是答案
|
|
|
|
|
因为佳佳所有的亲戚都要拜访到,现在不知道的是什么样顺序拜访才是时间最少的。 把所有可能顺序都 **枚举** 出来,通过查表,找出两个亲戚家之间的最小时间,累加结果的和,再$PK$最小就是答案
|
|
|
|
|
|
|
|
|
|
#### 4.实现细节
|
|
|
|
|
通过前面的$6$次打表预处理,可以求出$6$个$dist$数组,当我们需要查找 $1->5$的最短路径时,直接查$dist[1][5]$
|
|
|
|
|
@ -102,7 +104,7 @@ void add(int a, int b, int c) {
|
|
|
|
|
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
int dist[6][N];
|
|
|
|
|
int dis[6][N];
|
|
|
|
|
int id[6]; // 0号索引:佳佳的家,其它5个亲戚,分别下标为1~5,值为所在的车站编号
|
|
|
|
|
|
|
|
|
|
/*
|
|
|
|
|
@ -113,13 +115,13 @@ bool st[N];
|
|
|
|
|
|
|
|
|
|
/*
|
|
|
|
|
S:出发车站编号
|
|
|
|
|
dist[]:是全局变量dist[6][N]的某一个二维,其实是一个一维数组
|
|
|
|
|
dis[]:是全局变量dis[6][N]的某一个二维,其实是一个一维数组
|
|
|
|
|
C++的特点:如果数组做参数传递的话,将直接修改原地址的数据
|
|
|
|
|
此数组传值方式可以让我们深入理解C++的二维数组本质:就是多个一维数组,给数组头就可以顺序找到其它相关数据
|
|
|
|
|
计算的结果:获取到S出发到其它各个站点的最短距离,记录到dist[S][站点号]中
|
|
|
|
|
计算的结果:获取到S出发到其它各个站点的最短距离,记录到dis[S][站点号]中
|
|
|
|
|
*/
|
|
|
|
|
void dijkstra(int S, int dist[]) {
|
|
|
|
|
dist[S] = 0;
|
|
|
|
|
void dijkstra(int S, int dis[]) {
|
|
|
|
|
dis[S] = 0;
|
|
|
|
|
memset(st, false, sizeof st);
|
|
|
|
|
priority_queue<PII, vector<PII>, greater<PII>> q;
|
|
|
|
|
q.push({0, S});
|
|
|
|
|
@ -132,9 +134,9 @@ void dijkstra(int S, int dist[]) {
|
|
|
|
|
st[u] = true;
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
int v = e[i];
|
|
|
|
|
if (dist[v] > dist[u] + w[i]) {
|
|
|
|
|
dist[v] = dist[u] + w[i];
|
|
|
|
|
q.push({dist[v], v});
|
|
|
|
|
if (dis[v] > dis[u] + w[i]) {
|
|
|
|
|
dis[v] = dis[u] + w[i];
|
|
|
|
|
q.push({dis[v], v});
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
@ -153,10 +155,10 @@ void dfs(int u, int pre, int sum) {
|
|
|
|
|
for (int i = 1; i <= 5; i++) // 在当前位置上,枚举每个可能出现在亲戚站点
|
|
|
|
|
if (!st[i]) { // 如果这个亲戚没走过
|
|
|
|
|
st[i] = true; // 走它
|
|
|
|
|
// 本位置填充完,下一个位置,需要传递前序是i,走过的路径和是sum+dist[pre][id[i]].因为提前打好表了,所以肯定是最小值,直接用就行了
|
|
|
|
|
// 本位置填充完,下一个位置,需要传递前序是i,走过的路径和是sum+dis[pre][id[i]].因为提前打好表了,所以肯定是最小值,直接用就行了
|
|
|
|
|
// 需要注意的是一维是 6的上限,也就是 佳佳家+五个亲戚 ,而不是 车站号(佳佳家+五个亲戚) !因为这样的话,数据就很大,数组开起来麻烦,可能会MLE
|
|
|
|
|
// 要注意学习使用小的数据标号进行事情描述的思想
|
|
|
|
|
dfs(u + 1, i, sum + dist[pre][id[i]]);
|
|
|
|
|
dfs(u + 1, i, sum + dis[pre][id[i]]);
|
|
|
|
|
st[i] = false; // 回溯
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
@ -178,10 +180,10 @@ int main() {
|
|
|
|
|
|
|
|
|
|
// 计算从某个亲戚所在的车站出发,到达其它几个点的最短路径
|
|
|
|
|
// 因为这样会产生多组最短距离,需要一个二维的数组进行存储
|
|
|
|
|
memset(dist, 0x3f, sizeof dist);
|
|
|
|
|
for (int i = 0; i < 6; i++) dijkstra(id[i], dist[i]);
|
|
|
|
|
memset(dis, 0x3f, sizeof dis);
|
|
|
|
|
for (int i = 0; i < 6; i++) dijkstra(id[i], dis[i]);
|
|
|
|
|
// 枚举每个亲戚所在的车站站点,多次Dijkstra,分别计算出以id[i]这个车站出发,到达其它点的最短距离,相当于打表
|
|
|
|
|
// 将结果距离保存到给定的二维数组dist的第二维中去,第一维是指从哪个车站点出发的意思
|
|
|
|
|
// 将结果距离保存到给定的二维数组dis的第二维中去,第一维是指从哪个车站点出发的意思
|
|
|
|
|
|
|
|
|
|
// dfs还要用这个st数组做其它用途,所以,需要再次的清空
|
|
|
|
|
memset(st, 0, sizeof st);
|
|
|
|
|
|