'commit'

TangDou/AcWing_TiGao/T5/QiWang/217.md

@@ -67,14 +67,20 @@ $f(i)$：从$i$跳到$N$的期望长度。边界$f(N)=0$
 ③ 所有贡献值累加和就是期望
 </h5></font> 
 
-#### 期望的线性性质
-$$\large E(aX+bY)=aE(X)+bE(Y)$$
 
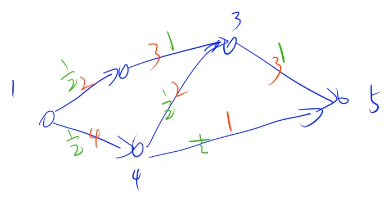
-根据本题题意我们可以进行递推
+**有向无环图**
+
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312191619342.png)
+
+事件发生的期望的线性性 $$\large E(aX+bY)=aE(X)+bE(Y)$$
+
+
+$f[i]$: 从 $i$ 跳到 $N$ 的期望长度
+边界: $f[N]=0$
+答案: $f[1]$
+
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312191621193.png)
 
-$f(i)$: 从 $i$ 跳到 $N$ 的期望长度
-边界: $f(N)=0$
-所求的答案: $f(1)$
 则有如下递推式：
 
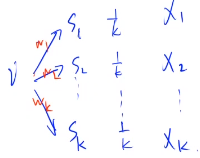
 $\large f(i)=E(\frac{1}{k}(w_1+x_1)+\frac{1}{k}(w_2+x_2)+⋯+\frac{1}{k}(w_k+x_k)) \\