'commit'

TangDou/Topic/【换根】dfs专题.md

@@ -825,7 +825,6 @@ int main() {
 
 #### [$POJ3585$ $Accumulation$ $Degree$](http://poj.org/problem?id=3585)
 
-
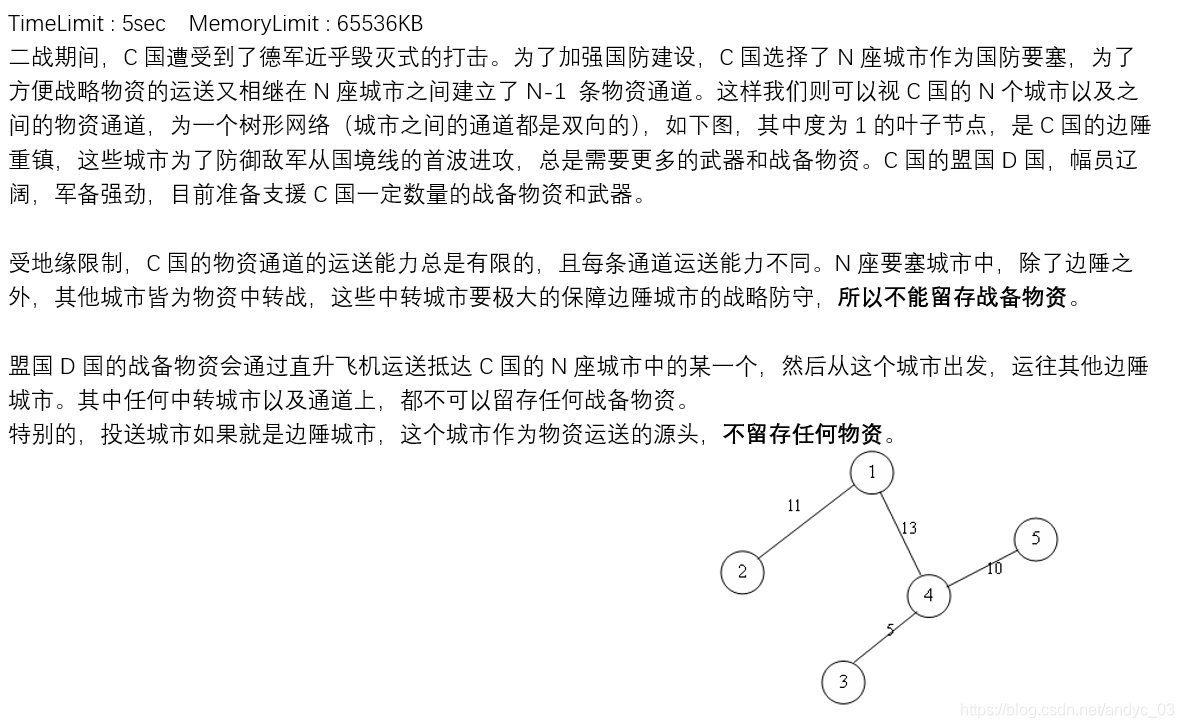
 **题意**
 ![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401161333814.png)
 
@@ -839,30 +838,43 @@ int main() {
 - 1.第一次扫描，任选一个点为根，在 **有根树** 上执行一次树形$DP$。
 - 2.第二次扫描，从刚才选出的根出发，对整棵树执行一次$DFS$，在每次递归前进行 **自上而下** 的推导，计算出 **换根** 之后的解。
 
+
+
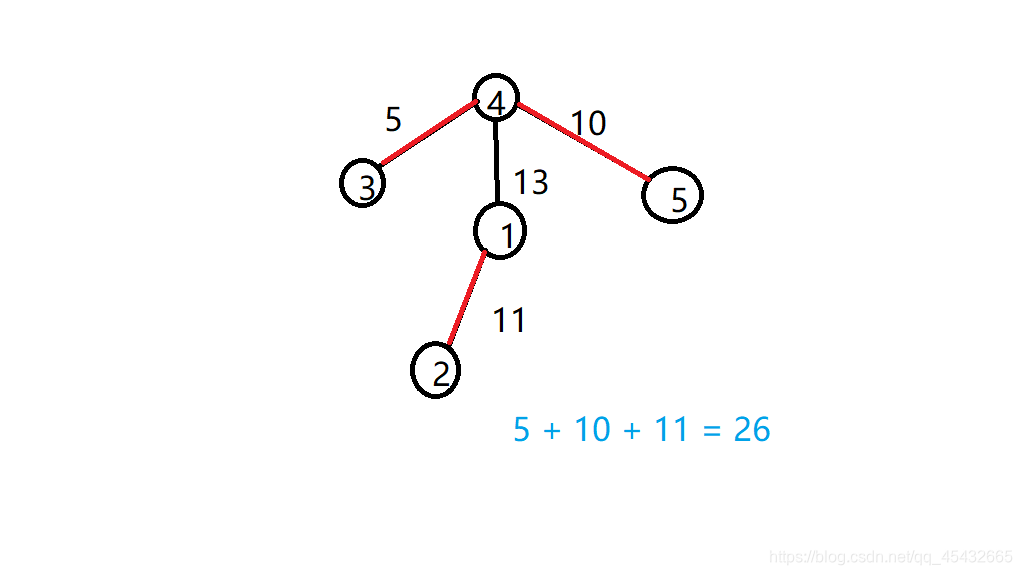
+**样例分析**
+$5$个点， $4$条边。当以$4$为起点时， 得到最大流量为$26$。
+
+![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401161338335.png)
+
+
 **本题思路**
-![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401161324729.png)
 
-![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401161325661.png)
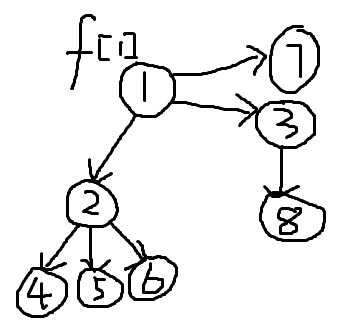
+- ① 选择$1$号节点当做根节点,做一次树形$DP$，至下往上进行状态转移，更新$f$数组的值，$f$数组存的是$f[i]$ 是 $i$的子树的最大流量(**向下的**)。
 
-首先，选择$1$号结点，然后树形$dfs$:
-- 1、求出$f$数组($f[i]$表示以$1$这根的树，以$i$为根的子树中流量的最大值)。
-- 2、设$g[u]$表示以$u$为源点，流向整个水系的最大流量，则显然$g[1]=f[1]$。
+- ② 因为$1$号节点没有向上的路径了，所以$g[1]=f[1]$  
+- ③ 从$1$号根节点出发, 扫描所有节点, 自顶往下进行更新$g$数组,$g[x]$代表以$x$为根节点的整棵树的最大总流量(**不光是向下，还要有向上的**)。
+       
+用$du$数组存节点的度,以便判断叶子结点:第一次搜索时,状态转移是如下代码所示:
+- ① 如果$v$是叶子结点， $v$的子树的最大流就是 $f[u] + w[u][v]$ 这里的$w[u][v]$表示$u$ 到 $v$ 的流量，代码中用$w[i]$表示
+- ② 如果$v$不是叶子结点， 流量就等于$v$的子树的最大流量和$u$到$v$的流量取最小值。
 
-假设$g[u]$已经求出，考虑其子结点$v$，则$g[v]$包含两部分：
-- 1.从$v$流向以$v$为根的子树的流量，已经计算出来。
-- 2.从$v$沿着到父节点$u$的河道，进而流向水系中其他部分的流量。
+```cpp {.line-numbers}
+   if(du[v] == 1) f[u] += w[i];
+   else f[u] += min(f[v], w[i]);
+```
 
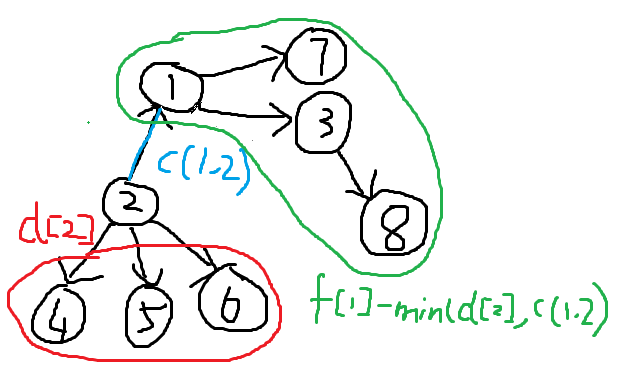
-由题意可得，从$u$流向$v$的流量为$min(f[v],c[u][v])$，所以从$u$流向除$v$以外其他部分的流量就是二者之差$g[u]−min(f[v],c[u][v])$。于是，把$v$作为源点，先流到$u$，再流向其他部分的流量就是把这个 **差** 再与$c[u][v]$取较小值后的结果。
+在进行$g$数组更新时也是类似的做法，由于是自上往下更新， 所以和上面会在更新存值时有一点不同，这里也是$u \rightarrow v$。
 
-$$
-\large \left\{\begin{matrix}
-g[v]=f[v]+min(g[u]−min(f[v],c[u][v])−c[u][v]) & du[u]>1 \\ 
-g[v]=f[v]+c[u][v] &  du[u]==1
-\end{matrix}\right.
-$$
+- ① 如果$u$是叶子结点,  $g[v] = f[v] + w[i]$
+- ② 如果$u$不是叶子结点$,g[u]$的总流量减去$u$流向$v$的最大流，这就是$u$流向另外节点的总流量，再在这个总流量，和$w[i]$取一个最小值，就是$v$流向$u$的最大流，再加上$v$流向其他节点的总流量，就是以$v$为根节点的这棵树的最大总流量。
 
-这是一个由上而下的递推方程，我们通过一次$dfs$即可实现。
+```cpp {.line-numbers}
+if (du[u] == 1)
+    g[v] = f[v] + w[i];
+else
+    g[v] = f[v] + min(g[u] - min(f[v], w[i]), w[i]);
+```
 
+**$Code$**
 ```cpp {.line-numbers}
 #include <iostream>
 #include <cstdio>