|
|
|
|
@ -113,8 +113,7 @@ void get_mobius2(LL n) {
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
#### 6、性质
|
|
|
|
|
然后就谈谈它的两条性质:
|
|
|
|
|
#### 6、性质$I$
|
|
|
|
|
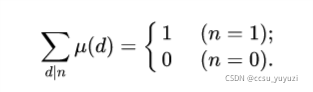
|
|
|
|
|
|
|
|
|
|
该图意为$n$的所有因子的莫比乌斯值的和只有在$n=1$时成立为$1$,其余通通为$0$;
|
|
|
|
|
@ -123,26 +122,27 @@ void get_mobius2(LL n) {
|
|
|
|
|
|
|
|
|
|
首先我们可以把$n$分解为很多个质数相乘(此时质数的幂不一定为$1$):
|
|
|
|
|
令 $\large n=p_1^ {a_1}* p_2^ {a_2}* ... *p_k^{a_k}$
|
|
|
|
|
因为这是对它们的莫比乌斯值的求和,这是求它所有约数的莫比乌斯值的和,就相当于在这么多的素数中依次选择一个两个三个......的质因子来相乘组成所有约数,但是根据莫比乌斯函数性质,包含有素数平方的约数不用计算,他对答案的贡献值为$0$,所以我们可以把$n$分解的质数的次数全部消除为$1$,只有当莫比乌斯值为$-1$或者$1$时才对结果有贡献.那么问题就单纯的变为在$k$个$n$的质因子中选$0$到$k$个值组成约数,再将这些约数的值相加:
|
|
|
|
|
|
|
|
|
|
$\displaystyle \sum_{d | n} \mu(d)$ 这是求$n$的所有约数的莫比乌斯函数值的和,相当于在$p_1,p_2,p_3,...$这些素数中选择若干个质因子相乘来组成所有约数。
|
|
|
|
|
|
|
|
|
|
根据莫比乌斯函数性质,包含有素数平方的约数不用计算,他对答案的贡献值为$0$,所以我们可以把$n$分解的质数的次数全部消除为$1$,只有当莫比乌斯值为$-1$或者$1$时才对结果有贡献.那么问题就单纯的变为在$k$个$n$的质因子中选$0$到$k$个值组成约数,再将这些约数的值相加:
|
|
|
|
|
|
|
|
|
|
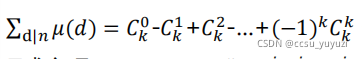
|
|
|
|
|
|
|
|
|
|
注意,这里的符号并不是全为加法,而是隔一个加隔一个减,这是因为莫比乌斯函数是积性函数,当选的数是奇数个时为值为负,反之为正,又因二项式定理,将$-1$和$1$带入,可以得到结果为$0$.
|
|
|
|
|
|
|
|
|
|
这里的式子就很像容斥定理了,那我顺便记录一下我理解的一小部分容斥定理:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
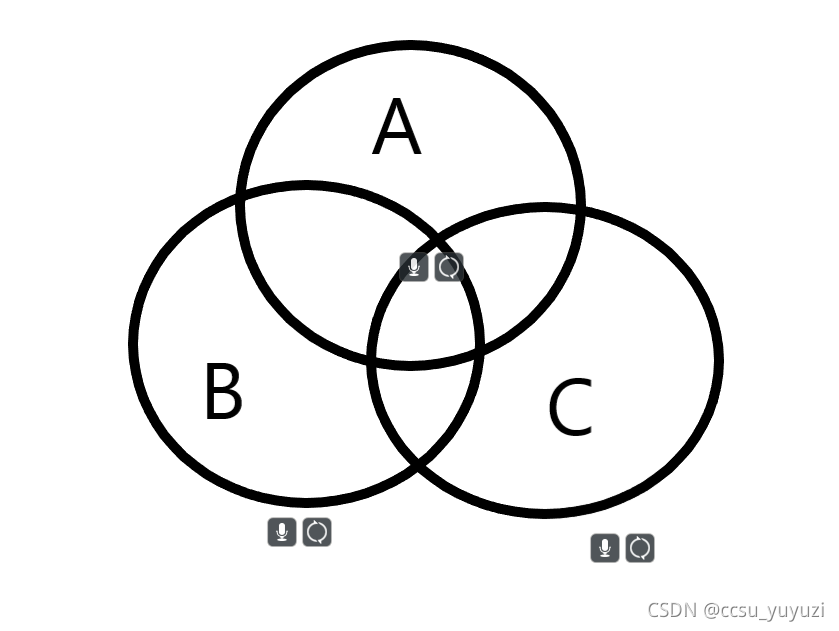
举个例子就好理解了,当我们要计算这个图形的面积,我们可以先计算$A,B,C$三个图形的面积的和,计算完之后我们会发现多计算了重叠部分,那么在尝试减去每两个相交的的图形的面积,这样每两两相交的面积被减去后,我们会发现,第一次算三个大面积时计算了三次的最中间的那个面积,在第二次减去两两相交的面积是有被减去了三次,就相当于没有计算了,这里就要再次加上最中间的这个面积,也就得到了图形总面积.大概就是这样的意思,当你计算某种含有多种性质的集合的时候(每个集合中元素可能有很多种性质),就可以这样计算.(其实还不是太懂,在下面例题的时候会有运用,它和莫比乌斯函数值的分布非常像).
|
|
|
|
|
|
|
|
|
|
(2)对任意正整数n
|
|
|
|
|
#### 7、性质$II$
|
|
|
|
|
对任意正整数n
|
|
|
|
|
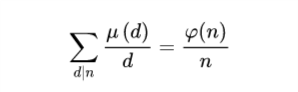
|
|
|
|
|
|
|
|
|
|
(ps:这条涉及莫比乌斯反演,还没学,学了再看)
|
|
|
|
|
|
|
|
|
|
好了,这就是大致知识,我学完了这个还是不知道这东西到底有什么用,还是得靠实战:
|
|
|
|
|
|
|
|
|
|
例题:[完全平方数](https://www.luogu.com.cn/problem/P4318)
|
|
|
|
|
#### 题单
|
|
|
|
|
**[完全平方数](https://www.luogu.com.cn/problem/P4318)**
|
|
|
|
|
|
|
|
|
|
题意就是筛去完全平方数及其的倍数,然后输出第k个的值.
|
|
|
|
|
|
|
|
|
|
|