diff --git a/TangDou/AcWing/BeiBao/1013.md b/TangDou/AcWing/BeiBao/1013.md
index 24632dc..b8fe2fb 100644
--- a/TangDou/AcWing/BeiBao/1013.md
+++ b/TangDou/AcWing/BeiBao/1013.md
@@ -124,11 +124,7 @@ $k$的含义是当前分组中的物品个数，是由小到大的。而这里
 
 
 ### 四、分组背包
-本题乍一看很像是 **背包$DP$**，为了转换成 **背包$DP$** 问题，我们需要对里面的一些叙述做出 **等价变换**
-
-**每家公司** 我们可以看一个 **物品组**，又因为 **所有公司** 最终能够被分配的 **机器数量** 是固定的
-
-<font color='red' size=5><b>思路转换</b></font>
+转换成 **背包$DP$** 问题，需要对里面的一些叙述做出 **等价变换**
 <font color='blue' size=4><b>
 ① 对于分给第$i$个公司的不同机器数量可以分别看作是一个物品组内的物品数量。
 
@@ -148,34 +144,6 @@ $k$的含义是当前分组中的物品个数，是由小到大的。而这里
 
 目标状态 ：$f[N][M]$
 
-#### 动态规划求状态转移路径
-这里我介绍一个从 **图论** 角度思考的方法
-
-**动态规划** 本质是在一个 **拓扑图** 内找 **最短路**
-
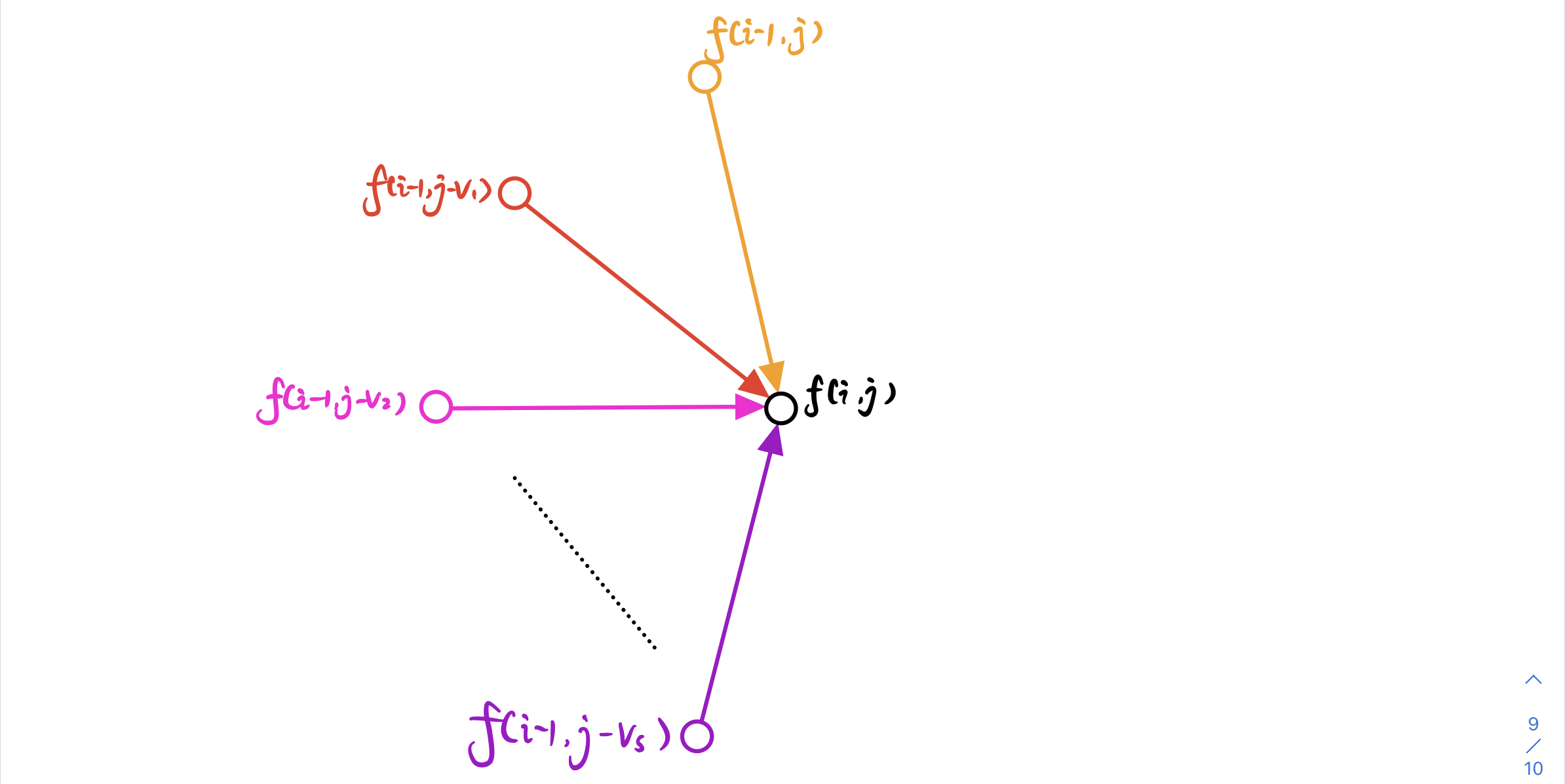
-我们可以把每个 **状态**$f[i][j]$看作一个 **点**，**状态的转移** 看作一条 **边**，把 **状态的值** 理解为 **最短路径长**
-
-具体如下图所示：
-![](https://cdn.acwing.com/media/article/image/2021/06/21/55909_00c396a1d2-IMG_7F8CDA59DBB8-1.jpeg)
-
-对于 **点** $f[i][j]$ 来说，他的 **最短路径长** 是通过所有到他的 **边** 更新出来的
-
-更新 **最短路** 的 **规则** 因题而已，本题的 **更新规则** 是 
-$$\large f(i,j)=max(f(i−1,j−v_i))+w_i$$
-
-最终，我们会把从 **初始状态**（起点）到 **目标状态** （终点）的 **最短路径长** 更新出来
-
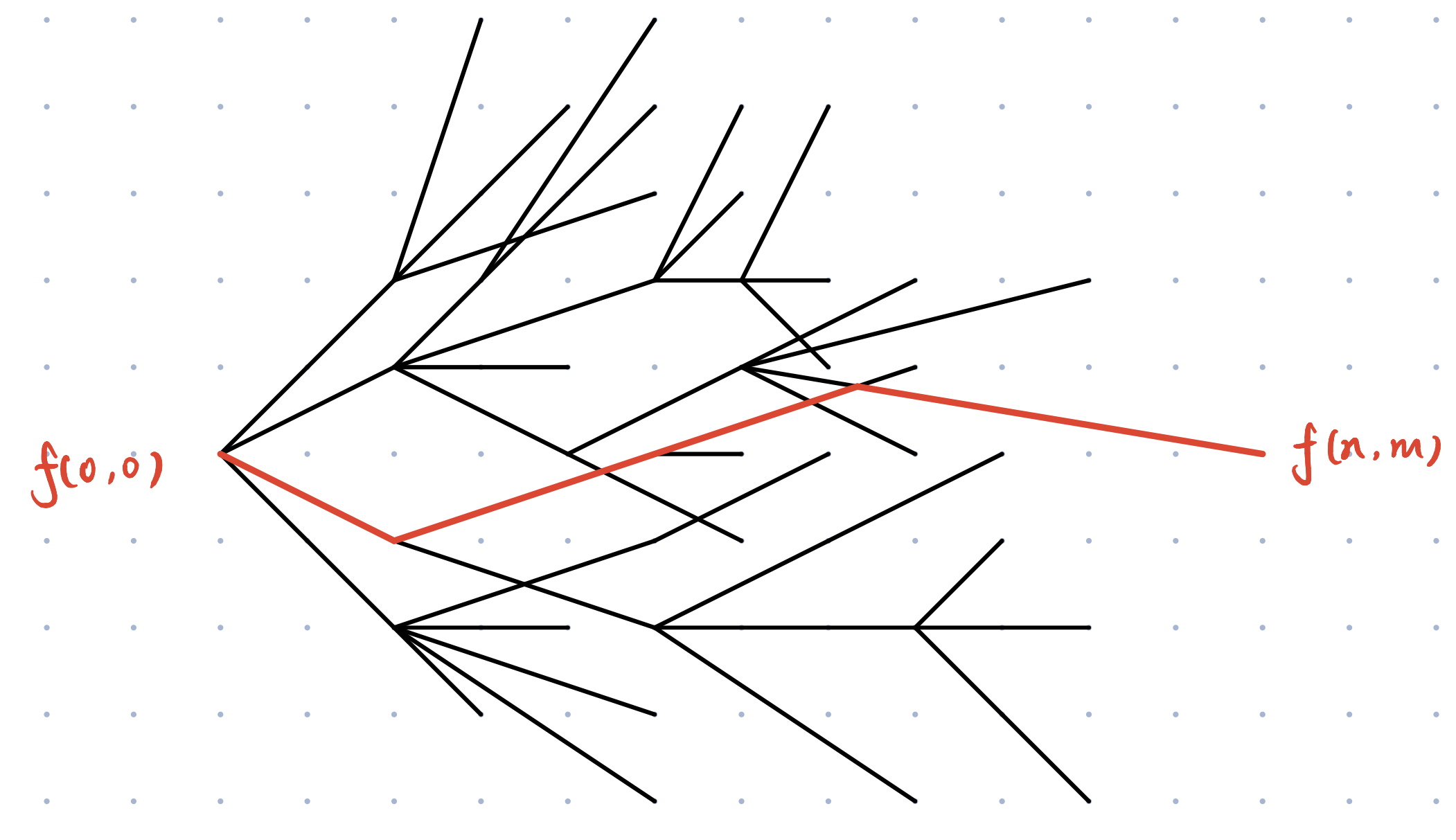
-随着这个更新的过程，也就在整个 **图** 中生成了一颗 **最短路径树**
-
-该 **最短路径树** 上 **起点** 到 **终点** 的 **路径** 就是我们要求的 **动态规划的状态转移路径**
-
-如下图所示：
-![](https://cdn.acwing.com/media/article/image/2021/06/21/55909_452b37cdd2-IMG_CFEE43CC6F3D-1.jpeg)
-
-那么 **动态规划求状态转移路径** 就变成了在 **拓扑图** 中找 **最短路径** 的问题了
-
-可以直接沿用 **最短路** 输出路径的方法就可以找出 **状态的转移**
-
 
 **二维数组写法**
 ```cpp {.line-numbers}
diff --git a/TangDou/AcWing/BeiBao/9.md b/TangDou/AcWing/BeiBao/9.md
index cc25707..5c8f049 100644
--- a/TangDou/AcWing/BeiBao/9.md
+++ b/TangDou/AcWing/BeiBao/9.md
@@ -3,7 +3,8 @@
 ### 一、题目描述
 有 $N$ 组物品和一个容量是 $V$ 的背包。
 
-每组物品有若干个，同一组内的物品最多只能选一个。
+每组物品有若干个，**同一组内的物品最多只能选一个**。
+
 每件物品的体积是 $v_{ij}$，价值是 $w_{ij}$，其中 $i$ 是组号，$j$ 是组内编号。
 
 求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
@@ -57,25 +58,19 @@ $0<v_{ij},w_{ij}≤100$
 #### 状态表示
 $f[i][j]$ 从前 $i$ 组物品中选择且总体积不大于 $j$ 的最大价值
 
-#### 状态计算
-  针对第 $i$ 组物品，将整个状态划分成 $s[i]+1$ 类：
-  * 第$i$组物品一个都不要：$f[i][j] = f[i-1][j]$
-  * 选第 $i$ 组物品的第一个物品：$f[i][j] = f[i-1][j-v[1]]+w[1]$
-  * 选第 $i$ 组物品的第二个物品：$f[i][j] = f[i-1][j-v[2]]+w[2]$
-  * 选第 $i$ 组物品的第 $k$ 个物品：$f[i][j] = f[i-1][j-v[k]]+w[k]$ 
-  
 #### 状态转移
-  $$\large f[i][j]=max(f[i][j], f[i-1][j-v[k]]+w[k])), k=0, 1, 2,...,s[i]$$
+  针对第 $i$ 组物品，将整个状态划分成 $s[i]+1$ 类：
+  * ① 第$i$组物品一个都不要：$f[i][j] = f[i-1][j]$
+  * ② 选第 $i$ 组物品的第一个物品：$f[i][j] = f[i-1][j-v_1]+w_1$
+  * ③ 选第 $i$ 组物品的第二个物品：$f[i][j] = f[i-1][j-v_2]+w_2$
+  * ④ 选第 $i$ 组物品的第 $k$ 个物品：$f[i][j] = f[i-1][j-v_k]+w_k$ 
+  * ...
 
-#### 状态初始化
-$f[0][0\sim m] = 0$ 表示在选择 `0` 件物品时对于任何体积来讲，其最大价值均为 `0`
+  $$\large f[i][j]=max(f[i][j], f[i-1][j-v_k]+w_k)) \  k \in [0, 1, 2,...,s_i]$$
 
-同理，分组背包问题也是可以从二维优化到一维的。其实只需要谨记两点：
-- **当前状态需要用上层状态转移时，从大到小枚举体积**
-- **当前状态需要用本层状态转移时，从小到大枚举体积**
+#### 初始化
+$f[0][0\sim m] = 0$ 表示在选择 `0` 组物品时对于任何体积来讲，其最大价值均为 `0`
 
-<font color='red' size=4><b>总结： 每个组中可以一个也不选，选也只能选择1个
-</b></font>
 
 ### 三、二维数组版本
 ```cpp {.line-numbers}
diff --git a/TangDou/AcWing/BeiBao/9_ErWei.cpp b/TangDou/AcWing/BeiBao/9_ErWei.cpp
index b503979..ea092f7 100644
--- a/TangDou/AcWing/BeiBao/9_ErWei.cpp
+++ b/TangDou/AcWing/BeiBao/9_ErWei.cpp
@@ -14,9 +14,10 @@ int main() {
             cin >> v[i][j] >> w[i][j]; // 第i个分组中物品的体积和价值
     }
 
-    for (int i = 1; i <= n; i++)
-        for (int j = 0; j <= m; j++) {
-            for (int k = 0; k <= s[i]; k++)
+    for (int i = 1; i <= n; i++)            // 每组
+        for (int j = 0; j <= m; j++) {      // 每个合法体积
+            f[i][j] = f[i - 1][j];          // 如果一个都不要，那么这一组就相当于白费，给你机会也不中用，继承于i-1
+            for (int k = 1; k <= s[i]; k++) // 选择第k个
                 if (j >= v[i][k])
                     f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]); // 枚举每一个PK一下大小
         }
diff --git a/TangDou/AcWing/BeiBao/背包问题专题.md b/TangDou/AcWing/BeiBao/背包问题专题.md
index 25a5624..e19a6a2 100644
--- a/TangDou/AcWing/BeiBao/背包问题专题.md
+++ b/TangDou/AcWing/BeiBao/背包问题专题.md
@@ -618,4 +618,11 @@ int main() {
     return 0;
 }
 
-```
\ No newline at end of file
+```
+
+### 八、分组背包
+**[$AcWing$ $9$. 分组背包问题](https://www.acwing.com/problem/content/description/9/)**
+
+
+**[$AcWing$ $1013$. 机器分配](https://www.acwing.com/problem/content/1015/)**
+分组背包求最优路径
\ No newline at end of file