|
|
|
|
@ -1,7 +1,7 @@
|
|
|
|
|
## [$AcWing$ $344$. 观光之旅](https://www.acwing.com/problem/content/346/)
|
|
|
|
|
|
|
|
|
|
### 一、题目描述
|
|
|
|
|
给定一张无向图,求图中一个 **至少包含 $3$ 个点** 的环,环上的节点不重复,并且环上的边的长度之和最小。
|
|
|
|
|
给定一张无向图,求图中一个至少包含 $3$ 个点的环,环上的节点不重复,并且环上的边的长度之和最小。
|
|
|
|
|
|
|
|
|
|
该问题称为 **无向图的最小环问题**。
|
|
|
|
|
|
|
|
|
|
@ -15,154 +15,138 @@
|
|
|
|
|
**输出格式**
|
|
|
|
|
输出占一行,包含最小环的所有节点(按顺序输出),如果不存在则输出 `No solution.`。
|
|
|
|
|
|
|
|
|
|
**数据范围**
|
|
|
|
|
$1≤N≤100,1≤M≤10000,1≤l<500$
|
|
|
|
|
### 二、$floyd + dp$求最小环模板题
|
|
|
|
|
|
|
|
|
|
**输入样例**:
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
5 7
|
|
|
|
|
1 4 1
|
|
|
|
|
1 3 300
|
|
|
|
|
3 1 10
|
|
|
|
|
1 2 16
|
|
|
|
|
2 3 100
|
|
|
|
|
2 5 15
|
|
|
|
|
5 3 20
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
**输出样例**:
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
1 3 5 2
|
|
|
|
|
```
|
|
|
|
|
**最优化问题**,**从集合角度考虑($DP$)**,**将所有环按编号最大的点** 分成 $n$ 类,**求出每类最小**,最后在类间取 $min$
|
|
|
|
|
|
|
|
|
|
### 二、算法思路
|
|
|
|
|
分类的标准是 **可重、不漏**。(对于求数量的问题,分类的标准是 **不重不漏**)
|
|
|
|
|
|
|
|
|
|
> 环上的节点不重复,并且环上的边的长度之和最小。
|
|
|
|
|
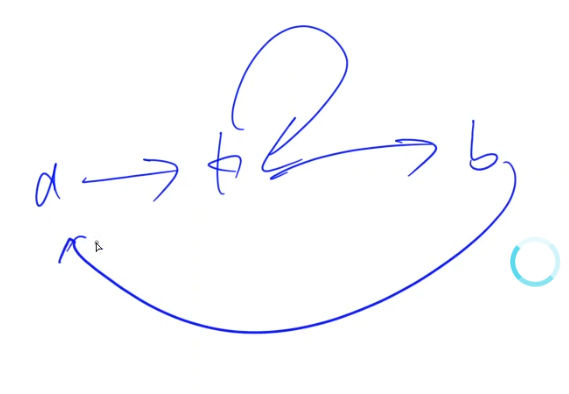
**解释**:
|
|
|
|
|
|
|
|
|
|
> 如果存在一个环,则上图中$k$出现多次,那么,如果去掉$k$身上的那个环,$a \rightarrow k \rightarrow b \rightarrow a $这个环的长度肯定是最小的。
|
|
|
|
|
|
|
|
|
|
最优化问题,可以从集合角度来思考,从集合角度来思考的一个好处就是:不容易丢东西。
|
|
|
|
|
#### 集合划分
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
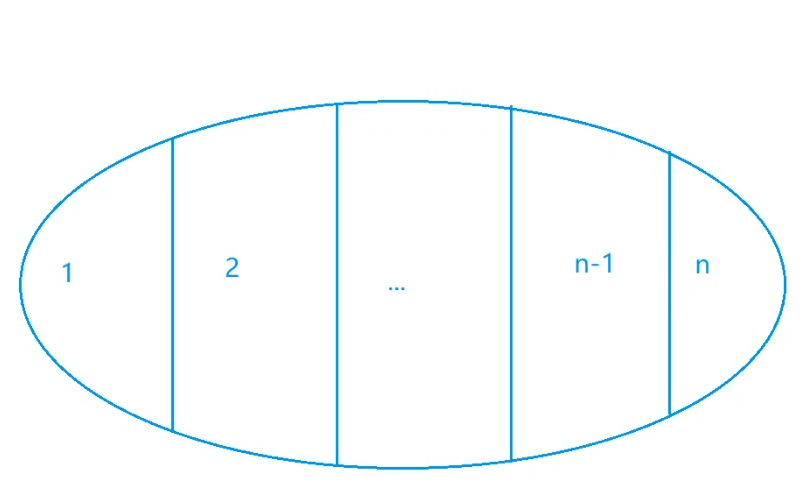
对于最大编号是 $k$ 的所有环,记点 $k$ 逆时针方向的前一点为 $i$,顺时针方向的下个点为 $j$。由于 $dis[i,k]=g[i,k], dis[k,j]=g[k,j]$ 为定值,要使整个环最小,就要使 $dis[i,j]$ 最小。
|
|
|
|
|
|
|
|
|
|
按 **环上编号最大点的编号** 为分类依据,分完类之后,只需要分别求一个每一类的最小值,然后求$min$所有最小值就是答案。
|
|
|
|
|
|
|
|
|
|
每一类的最小值怎么求呢?我们来回顾一下$floyd$的过程:
|
|
|
|
|
$floyd$ 第一层循环到 $k$ 时的 $dis[i,j]$ 恰好是中间点只包含 $1\sim k−1$ 的最短距离。因此第 $k$ 类最小值可在此时得到。
|
|
|
|
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
for(int k=1;k<=n;k++) //K是要插入的点,dis[i][j]数组相当是知道了i~j的只经过1~k-1这些点的最小路径
|
|
|
|
|
//此时在这个地方可以求第k类。从某个点连接到k
|
|
|
|
|
for(int i=1;i<=n;i++)
|
|
|
|
|
for(int j=1;j<=n;j++){
|
|
|
|
|
...
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
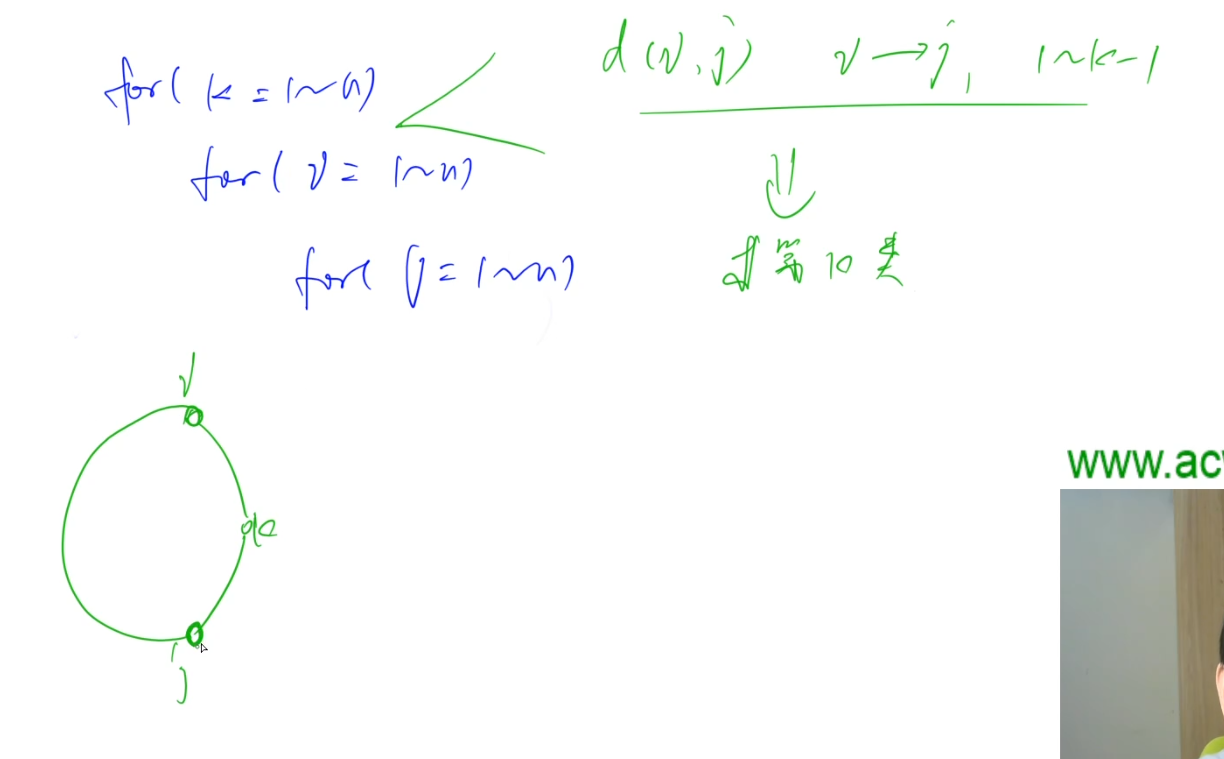
|
|
|
|
|
|
|
|
|
|
枚举一下所有的点对$(i,j)$,固定了$(i,j)$之后,那么$i \rightarrow k$,$k \rightarrow j$的长度都是固定的。
|
|
|
|
|
而左边那个弧的长度,就是$i \rightarrow j$在只有$1 \sim k-1$号点帮助下可以取得的最短距离,而这个距离恰好被保存在 **当前** 的$dis[i][j]$中。
|
|
|
|
|
#### 状态表示
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
也就是说,在正常进行$floyd$算法的第一层
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
for (int k = 1; k <= n ; k++){
|
|
|
|
|
//这里需要加上一些DP的动作,利用floyd进行dp转移
|
|
|
|
|
for (int i = 1; i < k; i++)
|
|
|
|
|
for (int j = i + 1; j < k; j++)
|
|
|
|
|
if (g[i][k] + g[k][j] < ans - dis[i][j]) // 减法防止爆INT
|
|
|
|
|
ans = dis[i][j] + g[i][k] + g[k][j];
|
|
|
|
|
|
|
|
|
|
for (int i = 1; i <= n; i++)
|
|
|
|
|
for (int j = 1;j <=n; j++){
|
|
|
|
|
....
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
#### 求方案
|
|
|
|
|
$DP$ 求方案一般要 **记录转移前驱的所有维**。但 $floyd$ 转移方程中的 $k$ 表示路径的中间点,由于路径可以被两端和中间点覆盖,只要记下中间点,就能递归出路径。
|
|
|
|
|
|
|
|
|
|
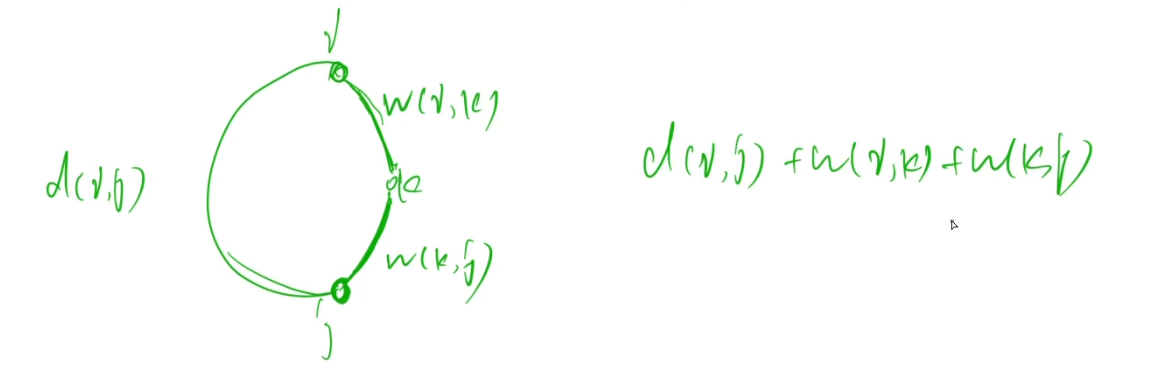
|
|
|
|
|
|
|
|
|
|
本题还有一个难点,就是$floyd$需要记录方案,其实就是求一下$d[i][j]$是由哪个中间点转移过来的。
|
|
|
|
|
****
|
|
|
|
|
|
|
|
|
|
#### $Code$
|
|
|
|
|
### 三、$floyd+dp+$递归输出路径
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
#include <cstring>
|
|
|
|
|
#include <iostream>
|
|
|
|
|
|
|
|
|
|
using namespace std;
|
|
|
|
|
const int N = 110, INF = 0x3f3f3f3f;
|
|
|
|
|
int n, m;
|
|
|
|
|
int g[N][N], dis[N][N];
|
|
|
|
|
vector<int> path;
|
|
|
|
|
int g[N][N], d[N][N];
|
|
|
|
|
int path[N], idx;
|
|
|
|
|
int mid[N][N];
|
|
|
|
|
int ans = INF;
|
|
|
|
|
|
|
|
|
|
// i->j之间的最短路径中途经点有哪些
|
|
|
|
|
void get_path(int i, int j) {
|
|
|
|
|
int k = mid[i][j]; // 获取中间转移点
|
|
|
|
|
if (!k) return; // 如果i,j之间没有中间点,停止
|
|
|
|
|
get_path(i, k); // 递归前半段
|
|
|
|
|
path.push_back(k); // 记录k节点
|
|
|
|
|
get_path(k, j); // 递归后半段
|
|
|
|
|
int k = mid[i][j]; //获取中间转移点
|
|
|
|
|
if (!k) return; //如果i,j之间没有中间点,停止
|
|
|
|
|
get_path(i, k); // i->k
|
|
|
|
|
path[idx++] = k; //记录k节点
|
|
|
|
|
get_path(k, j); // k->j
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
int main() {
|
|
|
|
|
// n个顶点,m条边
|
|
|
|
|
cin >> n >> m;
|
|
|
|
|
|
|
|
|
|
// 初始化邻接矩阵
|
|
|
|
|
memset(g, 0x3f, sizeof g);
|
|
|
|
|
for (int i = 1; i <= n; i++) g[i][i] = 0; // 邻接矩阵,自己到自己距离是0
|
|
|
|
|
for (int i = 1; i <= n; i++) g[i][i] = 0;
|
|
|
|
|
|
|
|
|
|
while (m--) {
|
|
|
|
|
int a, b, c;
|
|
|
|
|
cin >> a >> b >> c;
|
|
|
|
|
g[a][b] = g[b][a] = min(g[a][b], c); // 求最短路之类,(a,b)之间多条边输入只保留最短边
|
|
|
|
|
g[a][b] = g[b][a] = min(g[a][b], c);
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
// 把原始地图复制出来到生成最短距离dis
|
|
|
|
|
memcpy(dis, g, sizeof dis);
|
|
|
|
|
|
|
|
|
|
for (int k = 1; k <= n; k++) { // 枚举每一个引入点k来连接缩短i,j的距离
|
|
|
|
|
int ans = INF;
|
|
|
|
|
memcpy(d, g, sizeof d);
|
|
|
|
|
for (int k = 1; k <= n; k++) {
|
|
|
|
|
//插入DP计算
|
|
|
|
|
/*
|
|
|
|
|
Q1:为什么循环的时候i和j都需要小于k?
|
|
|
|
|
A:为了避免经过相同的点,比如i == k时,三个点就变成两个点了。
|
|
|
|
|
Q:为什么循环的时候i和j都需要小于k啊,Floyd不是只需要经过的点小于k就可以了吗
|
|
|
|
|
A:只是为了避免经过相同的点,比如i == k时,三个点就变成两个点了。
|
|
|
|
|
其实循环到n也是可以的,不过当i, j, k中有两个相同时就要continue一下
|
|
|
|
|
|
|
|
|
|
Q2:为什么非得把DP的这段代码嵌入到Floyd的整体代码中,不能先Floyd后再进行DP吗?
|
|
|
|
|
A:是不可以的。因为在进行插入节点号为k时,其实dis[i][j]中记录的是1~k-1插点后的最小距离,
|
|
|
|
|
而不是全部插入点后的最短距离。
|
|
|
|
|
*/
|
|
|
|
|
for (int i = 1; i < k; i++)
|
|
|
|
|
for (int j = i + 1; j < k; j++)
|
|
|
|
|
if (g[i][k] + g[k][j] < ans - dis[i][j]) { // 减法防止爆INT
|
|
|
|
|
ans = dis[i][j] + g[i][k] + g[k][j];
|
|
|
|
|
// 找到更小的环,需要记录路径,并且要求: 最小环的所有节点(按顺序输出)
|
|
|
|
|
// 顺序
|
|
|
|
|
// 1. 上面的i,j枚举逻辑是j>i,所以i是第一个
|
|
|
|
|
// 2. i->j 中间的路线不明,需要用get_path进行查询出i->j的最短路径怎么走,当然,也是在<k的范围内的
|
|
|
|
|
// 3. 记录j
|
|
|
|
|
// 4. 记录k
|
|
|
|
|
path.clear();
|
|
|
|
|
path.push_back(i);
|
|
|
|
|
get_path(i, j); // i是怎么到达j的?就是问dis[i][j]是怎么获取到的,这是在求最短路径过程中的一个路径记录问题
|
|
|
|
|
path.push_back(j);
|
|
|
|
|
path.push_back(k);
|
|
|
|
|
|
|
|
|
|
if (g[j][k] + g[k][i] < ans - d[i][j]) {
|
|
|
|
|
ans = d[i][j] + g[j][k] + g[k][i];
|
|
|
|
|
|
|
|
|
|
//找到更小的环,需要记录路径
|
|
|
|
|
//最小环的所有节点(按顺序输出)
|
|
|
|
|
//下面的记录顺序很重要:
|
|
|
|
|
// 1. 上面的i,j枚举逻辑是j>i,所以i是第一个
|
|
|
|
|
// 2. i->j 中间的路线不明,需要用get_path进行探索
|
|
|
|
|
// 3. 记录j
|
|
|
|
|
// 4. 记录k
|
|
|
|
|
idx = 0;
|
|
|
|
|
path[idx++] = i;
|
|
|
|
|
get_path(i, j); // i是怎么到达j的?就是问dist[i,j]是怎么获取到的,这是在求最短路径过程中的一个路径记录问题
|
|
|
|
|
path[idx++] = j;
|
|
|
|
|
path[idx++] = k;
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
// 正常floyd
|
|
|
|
|
//正常的floyd
|
|
|
|
|
for (int i = 1; i <= n; i++)
|
|
|
|
|
for (int j = 1; j <= n; j++)
|
|
|
|
|
if (dis[i][j] > dis[i][k] + dis[k][j]) {
|
|
|
|
|
dis[i][j] = dis[i][k] + dis[k][j];
|
|
|
|
|
mid[i][j] = k; // 记录路径i->j 是通过k进行转移的
|
|
|
|
|
if (d[i][j] > d[i][k] + d[k][j]) {
|
|
|
|
|
d[i][j] = d[i][k] + d[k][j];
|
|
|
|
|
mid[i][j] = k; //记录路径i->j 是通过k进行转移的
|
|
|
|
|
}
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
if (ans == INF)
|
|
|
|
|
puts("No solution.");
|
|
|
|
|
else
|
|
|
|
|
for (int i = 0; i < path.size(); i++) cout << path[i] << ' ';
|
|
|
|
|
for (int i = 0; i < idx; i++) cout << path[i] << ' ';
|
|
|
|
|
|
|
|
|
|
return 0;
|
|
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
### 四、关于三个$INF$相加爆$INT$的应对之道
|
|
|
|
|
$Q1$:为什么这里是用$ans-dis[i,j]$,而不是写成 $ans> dis[i,j]+g[j,k]+g[k,i]$?
|
|
|
|
|
$A$: $g[j][k],g[k][i] ∈ l$,$l$是小于$500$的,所在 $g[j][k]+g[k][i]<1000$,肯定没问题
|
|
|
|
|
$dis[i,j]$的初始值是$INF$,$g[i,j]$的初始值也是$INF$,如果都写在左边,如果$i,j,k$三者之间没有边,就是三个$INF$,累加和会爆掉$INT$,就会进入判断条件,错误. 而两个$INF$相加不会爆$INT$(想想松弛操作~)
|
|
|
|
|
|
|
|
|
|
$Q2:(LL) dis[i][j] + g[j][k] + g[k][i] < ans$ 为什么是正确的?而
|
|
|
|
|
$(LL) (dis[i][j] + g[j][k] + g[k][i]) < ans$为什么就是错误的?
|
|
|
|
|
$A$:
|
|
|
|
|
`INT_MAX = 2147483647`
|
|
|
|
|
`LONG LONG MAX=9223372036854775807ll`
|
|
|
|
|
|
|
|
|
|
`INF = 0x3f3f3f3f = 1061109567`
|
|
|
|
|
`INF * 3 =1061109567 * 3 = 3183328701` 大于`INT_MAX`,即会爆`INT`,需要开`LONG LONG`
|
|
|
|
|
|
|
|
|
|
`(LL)a + b + c` 将`a`转为`LL`,然后再加`b`加`c`,都是`LL+int`,在`LL`范围内,结果正确
|
|
|
|
|
`(LL)(a + b + c)` 是先计算`a+b+c`,先爆`INT`,再转换`LL`,结果错误。
|
|
|
|
|
|
|
|
|
|
$Q3$: 所有数据全开$LL$为什么一样不对呢?
|
|
|
|
|
$A:$
|
|
|
|
|
```c++
|
|
|
|
|
memset(q, 0x3f, sizeof q);
|
|
|
|
|
cout << q[0] << endl; // 4557430888798830399
|
|
|
|
|
cout << q[0] * 3 << endl; //-4774451407313060419
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
因为问题出在$LL$的初始$memset$上,比如`memset(q,0x3f,sizeof q);`
|
|
|
|
|
此时,每个数组位置上的值是:$4557430888798830399$
|
|
|
|
|
如果$i,j,k$三者之间没有关系,就会出现 类似于 `g[i,k]+g[k,j]+d[i,j]=3* 4557430888798830399`的情况,这个值太大,$LL$也装不下,值为`-4774451407313060419`,而此时$ans$等于$INF$,肯定满足小于条件,就进入了错误的判断逻辑。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
解决的办法有两种:
|
|
|
|
|
* `g[j][k] + g[k][i] < ans - dis[i][j]` 以减法避开三个$INF$相加,两个$INF$相加是$OK$的,不会爆$INT$
|
|
|
|
|
* 将运算前的$dis[i][j]$转为$LL$,这样,三个$INF$不会爆$LL$
|