huanghai
/
python
1
0
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity

'commit'

Browse Source
main
黄海 2 years ago
parent fe1e1b9cb1
commit 0d3c5f9dc0
4 changed files with 97 additions and 102 deletions
Show Stats Download Patch File Download Diff File

2
TangDou/AcWing_TiGao/T3/Floyd/344_3.cpp
Unescape View File

@ -67,4 +67,4 @@ int main() {
for (int i = 0; i < cnt; i++) printf("%d%s", ans[i], (i == cnt - 1) ? "\n" : " ");
}
return 0;
}
}

80
TangDou/Topic/HDU1385.cpp
Unescape View File

@ -1,64 +1,54 @@
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
const int INF = 0x3f3f3f3f;
// Floyd+记录起点后继
int n;
int g[N][N], w[N];
int path[N][N]; // 记录i到j最短路径中i的后继
const int N = 1003;
int g[N][N]; // 邻接矩阵
int n; // n个点
int w[N]; // 额外费用
int path[N][N]; // i->j 可能存在多条路线，我要找最短的。如果有多条最短的，我要字典序最小的。现在路线唯一了吧！比如这条路线最终是
// i->a->b->c->d->j,则path[i][j]=a,也就是第一个后继节点。
void floyd() {
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
if (g[i][k] != INF) // floyd优化
for (int j = 1; j <= n; j++) {
if (g[i][j] > g[i][k] + g[k][j] + w[k]) { // w[k]:点权
g[i][j] = g[i][k] + g[k][j] + w[k]; // k的加入，使得i->j的路径变短
path[i][j] = path[i][k]; // 如果i->k->j使得i->j更近，那么根据定义path[i][j]就是这条最短路径中距离i最近的那个点，而这个点由于是出现在i->k的必经之路上，而且是i->k的首席弟子，所以，也必然是i->j的首席弟子。
}
// 处理字典序
if (g[i][j] == g[i][k] + g[k][j] + w[k]) { // 如果存在多条最短路径，也就是，除了k还有其它k1,k2使得i->j距离一样小
if (path[i][j] > path[i][k]) path[i][j] = path[i][k]; // 字典序，谁更小就留下谁
}
for (int j = 1; j <= n; j++) {
if (g[i][j] > g[i][k] + g[k][j] + w[k]) {
g[i][j] = g[i][k] + g[k][j] + w[k];
path[i][j] = path[i][k]; // i->j这条最短路径上，i后面第一个节点，是i->k路径上第一个节点
}
// 相同路径下选择后继更小的(为了字典序)
if (g[i][j] == g[i][k] + g[k][j] + w[k])
if (path[i][j] > path[i][k])
path[i][j] = path[i][k];
}
}
// 递归输出路径
void print(int s, int e) {
printf("-->%d", path[s][e]); // 输出s的后继
if (path[s][e] != e) // 如果不是直连
print(path[s][e], e); // 递归输出后继
}
int main() {
while (cin >> n && n) {
for (int i = 1; i <= n; i++) {
while (cin >> n, n) {
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
path[i][j] = j; // 路径初始化,记录整条路径上，离i节点最近的，最短路径上的下一个点，只有i->j时，下一个点可不就是j
cin >> g[i][j]; // 不管是不是有边，都先录进来
if (g[i][j] == -1) g[i][j] = INF; // 如果题目中给出的是无边，那么设置为正无穷。此时，有些记录的path[i][j]就是没用的，但没事，后面会被其它代码替换掉path[i][j]。
cin >> g[i][j];
if (g[i][j] == -1) g[i][j] = INF;
path[i][j] = j;
}
}
for (int i = 1; i <= n; i++) cin >> w[i]; // 读入点权
// 多源最短路径
for (int i = 1; i <= n; i++) cin >> w[i];
floyd();
// 处理询问
int x, y;
while (cin >> x >> y) {
if (x == -1 && y == -1) break;
printf("From %d to %d :\n", x, y);
printf("Path: %d", x);
int u = x, v = y;
// 理解路径思路:
// (1) 从起点x出发,用循环打印路径,最后一个打印的肯定是y
// (2) 从起点x出发,第二个点应该是离x最近的，并且是最短路径上的那个点,这个点就是path[x][y]!
// path[x][y]：从起点x出发，到终点y有多条最短路径，我们选择字典序最小的那条最短路径，然后path[x][y]就是从x出发，离x最近的这条最短路径上的点。
while (x != y) {
printf("-->%d", path[x][y]); // 输出距离x最近的那个点
x = path[x][y]; // 更换x概念，向y逼近，让循环跑起来
}
int s, e;
puts("");
if (g[u][v] < INF)
printf("Total cost : %d\n", g[u][v]);
else
puts("-1");
puts("");
while (cin >> s >> e, ~s && ~e) {
printf("From %d to %d :\n", s, e);
printf("Path: %d", s);
if (s != e) print(s, e); // 起点与终点不同开始递归
printf("\nTotal cost : %d\n\n", g[s][e]);
}
}
return 0;

111
TangDou/Topic/【Floyd专题】.md
Unescape View File

@ -106,21 +106,21 @@ $floyd$ 算法求最短路（边权可为负）很优美，四行代码就搞定
开一个 $path$数组，$path[i][j]$ 表示：更新从 $i$ 到 $j$ 的最短路径时，经过的一个中转点。
```cpp {.line-numbers}
void floyd(){
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(dis[i][j]>dis[i][k]+dis[k][j]){
dis[i][j]=dis[i][k]+dis[k][j];
path[i][j]=k;
}
void floyd() {
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (dis[i][j] > dis[i][k] + dis[k][j]) {
dis[i][j] = dis[i][k] + dis[k][j];
path[i][j] = k; //记录i->j是通过k转移的
}
}
```
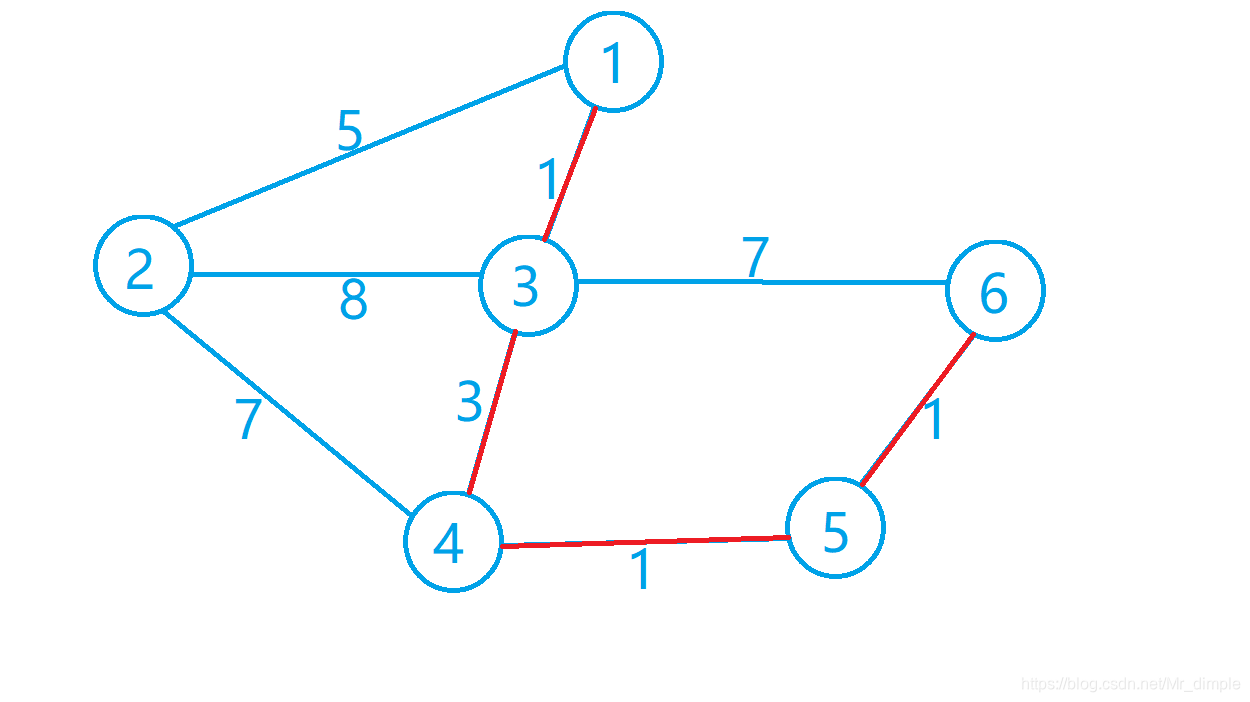
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401050754691.png)
在这个图中，很容易看出，从 $1$ 到 $6$ 之间的最短路径是标红的那几条边。
二重循环所有点，我们输出 $path$ 数组：
二重循环所有点，输出 $path$ 数组：
```cpp {.line-numbers}
0 0 0 3 4 5
0 0 0 0 4 5
@ -129,7 +129,7 @@ void floyd(){
0 0 0 0 0 0
0 0 0 0 0 0
```
可以看出，$path[1][6]$ 是 $5$，$path[1][5]$ 是 $4$，$path[1][4]$ 是 $3$。那么，最终 $path[i][j]$ 中存的就是 **从$i$到$j$的最短路径中的最后一个点**。
可以看出，$path[1][6]$ 是 $5$，$path[1][5]$ 是 $4$，$path[1][4]$ 是 $3$。那么，最终 $path[i][j]$ 中存的就是 **从$i$到$j$的最短路径中的靠近$j$的最后一个点**。
而我们最终输出路径的思路就是，不断分段最短路径！ 最后输出所有的点。
> **原理：由 $i$ 到 $j$ 的最短路径中的一点 $k$，将最短路径分段为从 $i$ 到 $k$ 的最短路径 和 从 $k$ 到 $j$ 的最短路径，最短路径就为从$i$到$k$的最短路径+从$k$到$j$的最短路径，一直分段，直到分到 $i$ 和 $j$ 为同一点，停止**
@ -137,31 +137,32 @@ void floyd(){
可能现在你有些迷糊，我们直接看代码吧！
```cpp {.line-numbers}
void get_path(int i,int j){//path[i][j]:从i到j最短路径中经过的一点k
if(i==j) return; //分段到同一点，停止
if(path[i][j]==0) cout<<i<<" "<<j<<endl;//i和j直接相连，则就是最短路径中的边（i到j最短路径不经过任何点）
else{
get_path(i,path[i][j]); //分段到从i到k的最短路径，
//输出从i到k最短路径中的所有点（一定都在从i到j的最短路径中）
get_path(path[i][j],j); //分段到从k到j的最短路径，
//输出从j到k最短路径中的所有的点
}
void print(int i, int j) { // path[i][j]:从i到j最短路径中经过的一点k
if (i == j) return; // 分段到同一点，递归结束
if (path[i][j] == 0) // i和j直接相连，就是i到j最短路径不经过任何点
cout << i << " " << j << endl;
else {
print(i, path[i][j]); // 分段输出从i到k的最短路径
// 输出从i到k最短路径中的所有点（一定都在从i到j的最短路径中）
print(path[i][j], j); // 分段输出从k到j的最短路径
// 输出从j到k最短路径中的所有的点
}
}
```
就是一个递归的过程。
就是一个 **递归** 的过程。
我们用上面的图模拟一下：
首先，从 1 到 6 的最短路径，pass[1][6]中存的是：该最短路径中的最后一个节点 5，即，k = 5。
首先，从 $1$ 到 $6$ 的最短路径，$path[1][6]$中存的是：该最短路径中的最后一个节点 $5$，即，$k = 5$。
那么，递归（分段） 到，从 1到5的最短路 和 从5到6的最短路。
1、从1到5的最短路，pass[1][5]=4，则又分段为从1到4的最短路和从4到5的最短路。
2、从1到4的最短路，pass[1][4]=3，则又分段为从1到3的最短路和从3到4的最短路。
3、pass[1][3]=0！如图，1和3直接相连！那么1和3都是最短路中的点，输出就行了！
那么，递归（分段） 到，从 $1$到$5$的最短路 和 从$5$到$6$的最短路。
- 从$1$到$5$的最短路，$path[1][5]=4$，则又分段为从$1$到$4$的最短路和从$4$到$5$的最短路。
- 从$1$到$4$的最短路，$path[1][4]=3$，则又分段为从$1$到$3$的最短路和从$3$到$4$的最短路。
- $path[1][3]=0$！如图，$1$和$3$直接相连！那么$1$和$3$都是最短路中的点，输出就行了！
回溯：
1、从3到4的最短路，pass[3][4]=0！3和4直接相连，3和4都是最短路中的点，输出！
2、从4到5的最短路，pass[4][5]=0！4和5直接相连，4和5都是最短路中的点，输出！
3、从5到6的最短路，pass[5][6]=0！5和6直接相连，5和6都是最短路中的点，输出！
**回溯**：
- 从$3$到$4$的最短路，$path[3][4]=0$！$3$和$4$直接相连，$3$和$4$都是最短路中的点，输出！
- 从$4$到$5$的最短路，$path[4][5]=0$！$4$和$5$直接相连，$4$和$5$都是最短路中的点，输出！
- 从$5$到$6$的最短路，$path[5][6]=0$！$5$和$6$直接相连，$5$和$6$都是最短路中的点，输出！
所以，最终输出的就是：
```cpp {.line-numbers}
@ -174,40 +175,38 @@ void get_path(int i,int j){//path[i][j]:从i到j最短路径中经过的一点k
**总体代码**
```cpp {.line-numbers}
void floyd(){
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(dist[i][j]>dist[i][k]+dist[k][j]){
dist[i][j]=dist[i][k]+dist[k][j];
pass[i][j]=k;
}
void floyd() {
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (dis[i][j] > dis[i][k] + dis[k][j]) {
dis[i][j] = dis[i][k] + dis[k][j];
path[i][j] = k;
}
}
void print(int i,int j){
if(i==j) return;
if(pass[i][j]==0) cout<<i<<" "<<j<<endl;
else{
print(i,pass[i][j]);
print(pass[i][j],j);
}
void print(int i, int j) {
if (i == j) return;
if (path[i][j] == 0)
cout << i << " " << j << endl;
else {
print(i, path[i][j]);
print(path[i][j], j);
}
}
int main(){
··· //一顿初始化，输入数据
floyd();
print(1,n); //输出从1到n的最短路径中的所有点（边）
return 0;
}
int main() {
··· //一顿初始化，输入数据
```
练习题：
floyd();
print(1, n); // 输出从1到n的最短路径中的所有点（边）
#### [$P2176$ $RoadBlock$ $S$](https://www.luogu.com.cn/problem/P2176)
```cpp {.line-numbers}
return 0;
}
```
**练习题**：
#### [$HDU-1385$ $Minimum$ $Transport$ $Cost$](http://acm.hdu.edu.cn/showproblem.php?pid=1385)

6
TangDou/Topic/【最短路径】Dijkstra算法专题.md
Unescape View File

@ -596,4 +596,10 @@ int main() {
cout << res << endl;
return 0;
}
```
$TODO$
#### [$P2176$ $RoadBlock$ $S$](https://www.luogu.com.cn/problem/P2176)
```cpp {.line-numbers}
```
Write Preview
Loading…
Cancel
Save