|
|
|
|
|
## [$AcWing$ $448$. 表达式的值](https://www.acwing.com/problem/content/450/)
|
|
|
|
|
|
|
|
|
|
|
|
### 一、题目描述
|
|
|
|
|
|
对于 $1$ 位二进制变量定义两种运算:
|
|
|
|
|
|
|
|
|
|
|
|
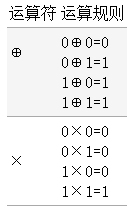
|
|
|
|
|
|
|
|
|
|
|
|
运算的优先级是:
|
|
|
|
|
|
|
|
|
|
|
|
先计算括号内的,再计算括号外的。
|
|
|
|
|
|
$×$ 运算优先于 $⊕$ 运算,即计算表达式时,先计算 $×$ 运算,再计算 $⊕$ 运算。
|
|
|
|
|
|
|
|
|
|
|
|
例如:计算表达式 $A⊕B×C$ 时,先计算 $B×C$,其结果再与 $A$ 做 $⊕$ 运算。
|
|
|
|
|
|
|
|
|
|
|
|
现给定一个未完成的表达式,例如 $\_+(\_*\_)$,请你在横线处填入数字 $0$ 或者 $1$,请问有多少种填法可以使得表达式的值为 $0$。
|
|
|
|
|
|
|
|
|
|
|
|
**输入格式**
|
|
|
|
|
|
第 $1$ 行为一个整数 $L$,表示给定的表达式中除去横线外的运算符和括号的个数。
|
|
|
|
|
|
|
|
|
|
|
|
第 $2$ 行为一个字符串包含 $L$ 个字符,其中只包含 $(、)、+、*$ 这 $4$ 种字符,其中 $(、)$ 是左右括号,$+、*$ 分别表示前面定义的运算符 $⊕$ 和 $×$。
|
|
|
|
|
|
|
|
|
|
|
|
这行字符按顺序给出了给定表达式中除去变量外的运算符和括号。
|
|
|
|
|
|
|
|
|
|
|
|
**输出格式**
|
|
|
|
|
|
输出包含一个整数,即所有的方案数。
|
|
|
|
|
|
|
|
|
|
|
|
注意:这个数可能会很大,请输出方案数对 $10007$ 取模后的结果。
|
|
|
|
|
|
|
|
|
|
|
|
**数据范围**
|
|
|
|
|
|
$0≤L≤10^5$
|
|
|
|
|
|
|
|
|
|
|
|
**输入样例**:
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
4
|
|
|
|
|
|
+(*)
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
**输出样例**:
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
3
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
### 二、题目解析
|
|
|
|
|
|
|
|
|
|
|
|
每一个中缀表达式都对应一棵满二叉树:
|
|
|
|
|
|
|
|
|
|
|
|
叶节点是数值;
|
|
|
|
|
|
内部节点是操作符,可能是$+, *$;
|
|
|
|
|
|
然后树形$DP$即可,每个节点存两个状态:该节点等于$0$的方案数、该节点等于$1$的方案数。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
这其实就是一个用公式递推的过程。每一步计算下一步答案为$0$或$1$的方法数:设两个步骤的运算结果经过每个符号到一个结果时,
|
|
|
|
|
|
- 第一个运算结果算出$0$的方案数为$a[0]$,$1$的方案数为$a[1]$。
|
|
|
|
|
|
- 第二个算出$0$的方案数为$b[0]$,算出$1$的方案数为$b[1]$
|
|
|
|
|
|
|
|
|
|
|
|
则有:
|
|
|
|
|
|
- 当符号是$⊕$时
|
|
|
|
|
|
- 得到$0$的方案数: $a[0]*b[0]$
|
|
|
|
|
|
- 得到$1$的方案数:$a[0]*b[1]+a[1]*b[0]+a[1]*b[1]$
|
|
|
|
|
|
|
|
|
|
|
|
- 当符号是$×$时
|
|
|
|
|
|
- 得到$0$的方案数:$a[0]*b[0]+a[0]*b[1]+a[1]*b[0]$
|
|
|
|
|
|
- 得到$1$的方案数:$a[1]*b[1]$
|
|
|
|
|
|
|
|
|
|
|
|
实际上我们也不需要将二叉树重建出来,直接在用栈模拟的过程中$DP$即可,这是因为栈模拟的顺序和深度优先遍历二叉树的顺序是相同的。
|
|
|
|
|
|
|
|
|
|
|
|
### 三、实现代码
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
|
|
|
|
|
|
|
|
|
const int N = 100010, mod = 10007;
|
|
|
|
|
|
|
|
|
|
|
|
/*
|
|
|
|
|
|
整体理解为一个表达式二叉树,每个节点是一个运算完的结果。
|
|
|
|
|
|
本题中要模拟的数字,在表达式二叉树中,其实是叶子节点,
|
|
|
|
|
|
stack<vector<int>> num; 中,入栈的每一个对象,其实都是一个只有两个
|
|
|
|
|
|
长度的小整数数组,分别是a[0],a[1],分别代表是0的方案数量,是1的方案数量
|
|
|
|
|
|
对于叶子节点而言,可以是1也可以是0,方案数量都是1种。
|
|
|
|
|
|
所以下面的代码中会有num.push({1, 1});
|
|
|
|
|
|
*/
|
|
|
|
|
|
stack<char> op; // 运算符栈
|
|
|
|
|
|
stack<vector<int>> num; // 得0的方案数num[0],得1的方案数num[1]
|
|
|
|
|
|
// 运算符优化级
|
|
|
|
|
|
unordered_map<char, int> h = {{'+', 1}, {'*', 2}};
|
|
|
|
|
|
|
|
|
|
|
|
void eval() {
|
|
|
|
|
|
// 运算符
|
|
|
|
|
|
auto c = op.top();
|
|
|
|
|
|
op.pop();
|
|
|
|
|
|
|
|
|
|
|
|
// 两个数,本题的弹出顺序不重要,事实上是先b后a,因为是栈
|
|
|
|
|
|
auto b = num.top();
|
|
|
|
|
|
num.pop();
|
|
|
|
|
|
auto a = num.top();
|
|
|
|
|
|
num.pop();
|
|
|
|
|
|
|
|
|
|
|
|
// ⊕ 运算符
|
|
|
|
|
|
if (c == '+')
|
|
|
|
|
|
num.push({a[0] * b[0] % mod,
|
|
|
|
|
|
(a[0] * b[1] + a[1] * b[0] + a[1] * b[1]) % mod});
|
|
|
|
|
|
else // × 运算符
|
|
|
|
|
|
num.push({(a[0] * b[0] + a[1] * b[0] + a[0] * b[1]) % mod,
|
|
|
|
|
|
a[1] * b[1] % mod});
|
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
|
|
int main() {
|
|
|
|
|
|
int n;
|
|
|
|
|
|
string expr;
|
|
|
|
|
|
cin >> n >> expr;
|
|
|
|
|
|
|
|
|
|
|
|
// 第一个位置,需要放上一个数字,可以是0也可以是1,方案数都是1
|
|
|
|
|
|
num.push({1, 1});
|
|
|
|
|
|
for (auto c : expr) { // 读入表达式
|
|
|
|
|
|
if (c == '(')
|
|
|
|
|
|
op.push(c); // 左括号入栈
|
|
|
|
|
|
else if (c == '+' || c == '*') {
|
|
|
|
|
|
// 通过while循环,把栈内的表达式先计算出结果,再将当前操作符入栈
|
|
|
|
|
|
while (op.size() && h[op.top()] >= h[c]) eval();
|
|
|
|
|
|
op.push(c);
|
|
|
|
|
|
// 处理完操作符,需要模拟下面的数字是0,还是1
|
|
|
|
|
|
num.push({1, 1}); // 无论是0还是1,方案数都是1,这样所有情况都考虑到了
|
|
|
|
|
|
} else { // 右括号
|
|
|
|
|
|
while (op.top() != '(') eval();
|
|
|
|
|
|
op.pop();
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
// 1*1-0 类似这样的表达式,op栈中应该有*-两种符号,需要再次弹栈计算
|
|
|
|
|
|
while (op.size()) eval();
|
|
|
|
|
|
cout << num.top()[0] << endl;
|
|
|
|
|
|
return 0;
|
|
|
|
|
|
}
|
|
|
|
|
|
```
|