python/TangDou/AcWing_TiGao/T5/ZhuHeJiShu/1310.md

##[$AcWing$ $1310$. 数三角形](https://www.acwing.com/problem/content/1312/)

### 一、题目描述
给定一个 $n×m$ 的网格，请计算三点都在格点上的三角形共有多少个。

下图为 $4×4$ 的网格上的一个三角形。

<center><img src='https://cdn.acwing.com/media/article/image/2020/01/02/19_b54c022e2d-a.png'></center>

**注意**：三角形的三点不能共线。

**输入格式**
输入一行，包含两个空格分隔的正整数 $m$ 和 $n$。

**输出格式**
输出一个正整数，为所求三角形数量。

**数据范围**
$1≤m,n≤1000$

**输入样例：**
```cpp {.line-numbers}
2 2
```
**输出样例：**
```cpp {.line-numbers}
76
```
### 二、引理

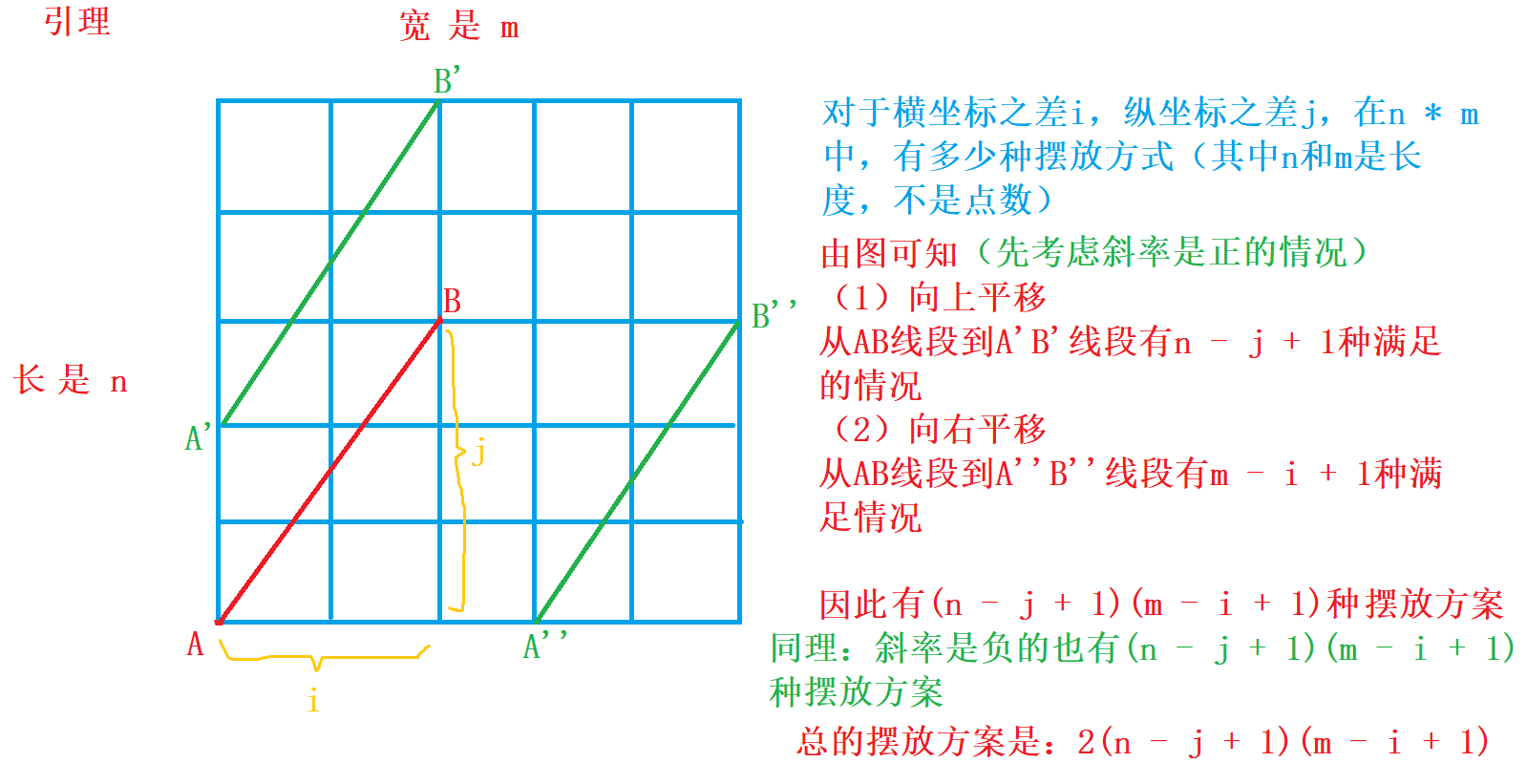
#### 引理$1$
<!-- ![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202311291611160.png) -->

![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202311291649456.png)


#### 引理$2$

如果　**左下角$(a,b)$**　和　**右上角$(c,d)$** 的点确定下来($a,b,c,d$都是整数)，则在线段$(a,b)->(c,d)$上，存在多少个整数位置的点$(x,y)$呢？
>**$Q$**:为啥要研究这个问题呢？因为这时产生的 **三点共线** 需要排除掉，这时无法构成三角形!

<font color='red' size=4><b>结论：</b></font>
整数位置上点的数量 $gcd(d-b,c-a)+1$个，如果不算两个端点，就是$gcd(d-b,c-a)-1$个。

**证明:**

<center><img src='https://cdn.acwing.com/media/article/image/2022/02/17/3138_48a3536f8f-%E4%B8%89%E8%A7%92%E5%BD%A2%E6%96%9C%E8%BE%B9%E7%82%B9%E4%B8%AA%E6%95%B0%E7%BB%93%E8%AE%BA%E8%A7%A3%E6%9E%901.png'></center>

对于斜边上的任何一点 $(x,y)$, 其满足：
$$\large \frac{y-b}{x-a}=\frac{d-b}{c-a} $$ 

注意：$a≤x≤c,b≤y≤d$

可知：$$\large \displaystyle y=\frac{d-b}{c-a}*(x-a)+b=\frac{\frac{d-b}{gcd(d-b,c-a)}}{\frac{c-a}{gcd(d-b,c-a)}}*(x-a)+b 
 \\
 \Rightarrow 
 \\
 y=\frac{d-b}{gcd(d-b,c-a)}*\frac{x-a}{\frac{c-a}{gcd(d-b,c-a)}}+b \ \ \  x  \in Z^+
$$

那么如果使得 $y∈Z^+$ 的话,必须使得 $\large \displaystyle \frac{c-a}{gcd(d-b,c-a)}|(x-a)$ $^{[1]}$，即：
$$\large x=\frac{c-a}{gcd(d-b,c-a)}*q+a$$

对于条件 $b≤y≤d$ 上述式子是由直线方程推出的，因此其在方程中等价于 $a≤x≤c$, 因此我们只需要考虑 $x$ 的范围限制即可:
$$\large a≤x=\frac{c-a}{gcd(d-b,c-a)}*q+a≤c  
$$

$$
\large \left\{\begin{matrix}
a-a \leq \frac{c-a}{gcd(d-b,c-a)}*q & \Rightarrow &0 \leq  \frac{c-a}{gcd(d-b,c-a)}*q & \ ①\\ 
\frac{c-a}{gcd(d-b,c-a)}*q \leq c-a & \Rightarrow & q \leq gcd(d-b,c-a)  & \ ②
\end{matrix}\right.
\\
\Rightarrow \\
 0 ≤ q ≤ gcd(d-b,c-a)
$$

$q$  可以取这个区间中的所有整数,即$[0,gcd(d-b,c-a)]$，数量=$gcd(d−b,c−a)+1$

然后我们分析对于区间中的任意一个点 $(x,y)$, 由于上面 $q$ 的范围可知 $a≤x≤c$, 因此均在斜边上不加上两个端点的话，就是 $gcd(d−b,c−a)−1$

> **解释**：$[1]$ 因为 $\frac{c-a}{gcd(d-b,c-a)}与\frac{d-b}{gcd(d-b,c-a)}$互质。


### 三、解题思路

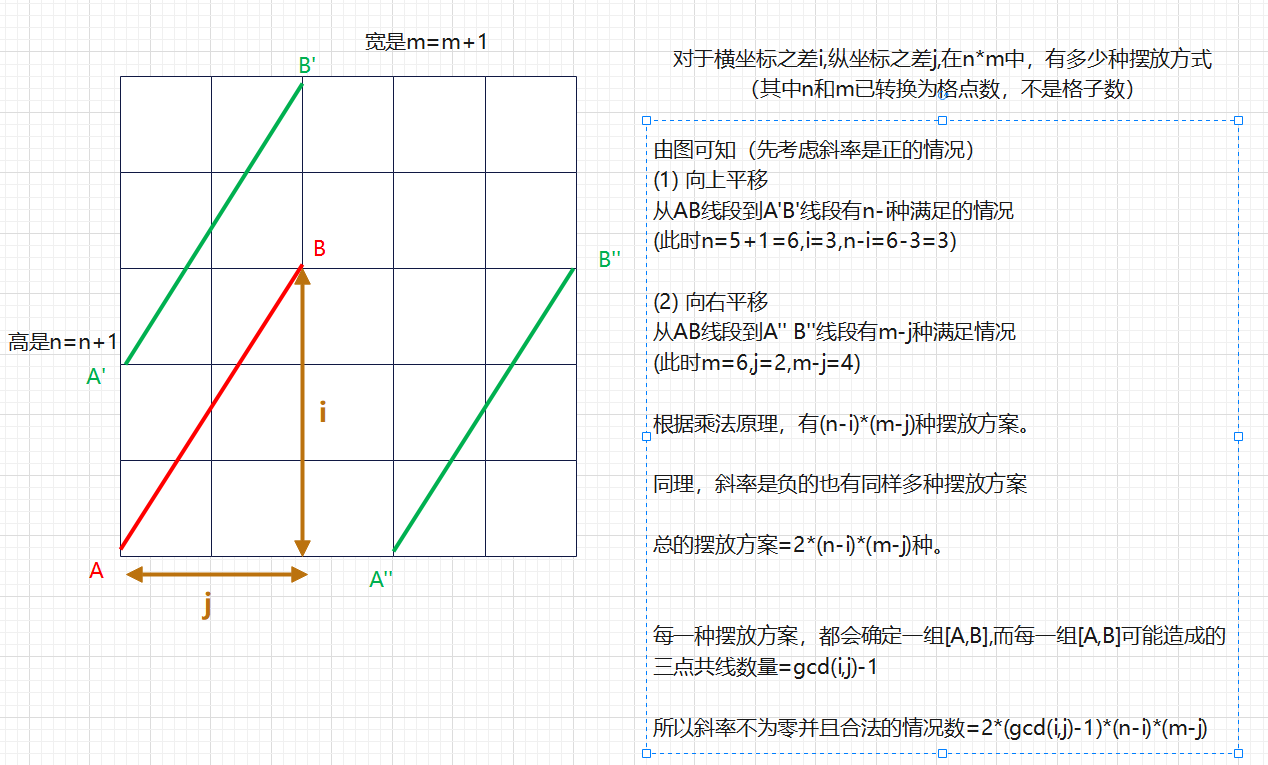
题目给定 长$n$，宽$m$的矩形，因此总端点数有$(n + 1) * (m + 1)$个，为编码方便，统一执行`m++,n++`,将**格子数转换成格点数**。

从总端点数选$3$个点的情况有$\large \displaystyle C_{n∗m}^3$种，再将不符合三角形规则的情况减去即可，即 **三角形的数目** = $\large \displaystyle C_{n∗m}^3$- **不满足要求的情况（三点共线）**

#### 不满足的情况(三点共线)

* ① **同一条横线**
  与$x$轴平行：$n\times C_m^3$

> **解释**：$m$个格点数中选择$3$个，一共有$C_m^3$种选法，同时，一共有$n$行，根据 **加法原理** ，就是 $n$个$C_m^3$相加，即$n \times C_m^3$

> **加法原理**:加法原理用于计算多个事件中至少发生一个的情况。可以理解为一个事件可以通过多种方式实现，每种方式有若干选择，最终的总选择数就是各种方式选择数的总和。区分乘法原理和加法原理的关键在于考虑的是事件的同时发生还是至少发生一个。
> 以本题为例，选择三个点，这三个点三点共线，如果是同一条横线，那么，如果发生在第$1$行,是$C_m^3$,如果发生在第$2$行，也是$C_m^3$,...,一件事说完就完事了，不是一个事情的多个步骤，**典型的加法原理**。

* ② **同一条竖线**
  与$y$轴平行：$m\times C_n^3$

* ③ **同一条斜线**
  **斜率为正**
    枚举左下角和右上角横纵坐标之差，计算在这两个点之间坐标是整数点的个数，可以构成这样两个点的方案是$(n−i)∗(m−j)$，两个点之间的整数点个数是$gcd(i,j)−1$，因此方案数:
    - $$(gcd(i,j)−1)∗(n−i)∗(m−j)$$
  - **斜率为负**
    - 与斜率为正相同。
     $$(gcd(i,j)−1)∗(n−i)∗(m−j)$$
  
  总数=- $$2*(gcd(i,j)−1)∗(n−i)∗(m−j)$$

#### 答案
  $$\large res=C_{(n+1)*(m+1)}^3-(n+1)*C_{m+1}^3-(m+1)*C_{n+1}^3-2*(gcd(i,j)−1)∗(n+1−i)∗(m+1−j) $$
由于提前$m++,n++$,所以可以简写为：
  $$\large res=C_{n*m}^3-n*C_{m}^3-m*C_{n}^3-2*(gcd(i,j)−1)∗(n−i)∗(m−j) $$


#### $Code$
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"

// C(n,3)计算公式
int C(int n) {
    return n * (n - 1) * (n - 2) / (3 * 2 * 1);
}

signed main() {
    int n, m;
    cin >> n >> m; // 行数,列数
    n++, m++;      // 将格子数转换成格点数,n->n+1,m->m+1

    int res = C(n * m) - n * C(m) - m * C(n);
    // 枚举所有高为i,宽为j的线段AB
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            res -= 2 * (__gcd(i, j) - 1) * (n - i) * (m - j);

    printf("%lld\n", res);
}

```
> 代码中$i,j$理解为 **左下角** 和 **右上角** 两个点的坐标差