python/TangDou/AcWing/SegmentTree/P2787.md

## [$P2787$ 语文$1$（$chin1$）- 理理思维](https://www.luogu.com.cn/problem/P2787)


### 题目背景

蒟蒻 $HansBug$ 在语文考场上，挠了无数次的头，可脑子里还是一片空白。

### 一、题目描述

考试开始了，可是蒟蒻 $HansBug$ 脑中还是一片空白。哦不！准确的说是乱七八糟的。现在首要任务就是帮蒟蒻 $HansBug$ 理理思维。假设 $HansBug$ 的思维是一长串字符串（字符串中包含且仅包含 $26$ 个字母），现在的你，有一张神奇的药方，上面依次包含了三种操作：

- 1、获取第 $x$ 到第 $y$ 个字符中字母 $k$ 出现了多少次

- 2、将第 $x$ 到第 $y$ 个字符全部赋值为字母 $k$

- 3、将第 $x$ 到第 $y$ 个字符按照 $\text{a} \sim \text{z}$ 的顺序排序


你欣喜若狂之时，可是他脑细胞和 $RP$ 已经因为之前过度紧张消耗殆尽，眼看试卷最后还有一篇八百字的作文呢，所以这个关键的任务就交给你啦！

#### 输入格式

第一行包含两个整数 $n,m$，分别表示 $HansBug$ 的思维所包含的字母个数和药方上操作个数。
第二行包含一个长度为 $n$ 的字符串，表示 $HansBug$ 的思维。

接下来 $m$ 行，每行表示一个操作，格式如下：

- `1 x y k` 表示将第 $x$ 到第 $y$ 个字符中 $k$ 出现的次数输出

- `2 x y k` 表示将第 $x$ 到第 $y$ 个字符全部替换为 $k$

- `3 x y` 表示将第 $x$ 到第 $y$ 个字符按照 $\text{a} \sim \text{z}$ 的顺序排序

#### 输出格式

输出为若干行，每行包含一个整数，依次为所有操作 $1$ 所得的结果。


#### 样例输入 #1

```
10 5
ABCDABCDCD
1 1 3 A
3 1 5
1 1 3 A
2 1 2 B
1 2 3 B
```

#### 样例输出 #1

```
1
2
2
```

#### 提示

样例说明：

 ![](https://cdn.luogu.com.cn/upload/pic/2231.png) 

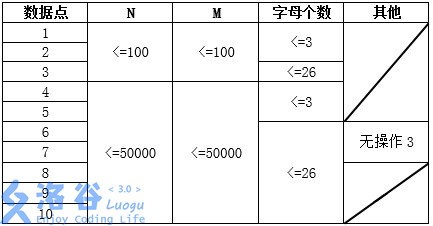
数据规模：

 ![](https://cdn.luogu.com.cn/upload/pic/2232.png) 

#### 此题目中大小写不敏感。

#### 新加了三组 hack 数据，不在上面的表格中，但保证 $1\le n,m \le 50000$。

### 二、线段树解法

这道题我的做法是线段树，由于只有$26$个字母，所以我们可以建 $26$ 个线段树。

对于操作 $1$ 我们维护一下区间和就可以了。

对于操作 $2$ 我们用 $lazy\_tag$ 就可以了

对于操作 $3$, 我们发现就是操作 $1$ 和操作 $2$ 的结合

值得一提的是，有两个剪枝优化能使程序快很多。

```cpp {.line-numbers}
int query(int u, int l, int r) {
    if (tr[u].sum == 0) return 0;                       // 整体加一块都是0，那你想查找子区间，也肯定是0，剪枝,不加这句，第12个测试点TLE
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum; // 如果完整命中, 返回现成的

    // 未能完整命中，有懒标记先下传懒标记，然后分裂
    if (tr[u].tag) pushdown(u);

    // 正常的查询
    if (tr[ls].r < l) return query(rs, l, r);
    if (tr[rs].l > r) return query(ls, l, r);
    return query(ls, l, r) + query(rs, l, r);
}

void modify(int u, int l, int r, int tag) {
    if (tr[u].tag == tag) return; // 剪枝,否则无法通过12测试点
    // 区间都修改为统一的值，如果上一次你修改成了1，本次还是修改成了1，那么只留同样的就可以了，不用再重新标识

    // 完整命中，修改自己的懒标记和统计信息
    if (tr[u].l >= l && tr[u].r <= r) {
        update(u, tag);
        return;
    }

    // 未能完整命中，有懒标记先下传懒标记，然后分裂
    if (tr[u].tag) pushdown(u);
    if (tr[ls].r >= l) modify(ls, l, r, tag);
    if (tr[rs].l <= r) modify(rs, l, r, tag);
    pushup(u);
}
```

这 $2$ 个剪枝虽然非常显然，但可以使程序快很多
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 1e5 + 10;

int n, m, f[26];
char a[N]; // 初始化输入的字符串

// 多棵线段树法
#define ls (u << 1)
#define rs (u << 1 | 1)
#define mid ((l + r) >> 1)
struct Tree {
    struct Node {
        int l, r, len; // 区间范围
        int sum;       // 区间和
        int tag;       // 懒标记
    } tr[N << 2];

    void pushup(int u) {
        tr[u].sum = tr[ls].sum + tr[rs].sum; // 汇总区间
    }

    // 修改u节点的懒标记和统计信息
    void change(int u, int tag) {
        tr[u].tag = tag;
        if (tr[u].tag == 1) tr[u].sum = tr[u].len;
        if (tr[u].tag == 0) tr[u].sum = 0;
    }

    void pushdown(int u) {
        if (~tr[u].tag) {
            // 向左儿子传递
            change(ls, tr[u].tag);
            // 向左儿子传递
            change(rs, tr[u].tag);
            // 终于完成向左右儿子传递懒标记的任务，将自己的懒标记清除
            tr[u].tag = -1;
        }
    }

    void build(int u, int l, int r) {
        tr[u].l = l, tr[u].r = r, tr[u].len = r - l + 1; // 整体区间[1,n]，管辖区间[l,r]
        tr[u].tag = -1;
        if (l == r) return;
        build(ls, l, mid);
        build(rs, mid + 1, r);
    }

    void modify(int u, int L, int R, int v) {
        if (tr[u].tag == v) return; // 剪枝,否则无法通过12测试点
        // 区间都修改为统一的值，如果上一次你修改成了1，本次还是修改成了1，那么只留同样的就可以了，不用再重新标识

        // 完整命中，修改自己的懒标记和统计信息
        int l = tr[u].l, r = tr[u].r;
        if (l > R || r < L) return;
        if (l >= L && r <= R) {
            change(u, v);
            return;
        }
        pushdown(u);
        modify(ls, L, R, v), modify(rs, L, R, v);
        pushup(u);
    }

    int query(int u, int L, int R) {
        if (tr[u].sum == 0) return 0; // 整体加一块都是0，那你想查找子区间，也肯定是0，剪枝,不加这句，第12个测试点TLE

        int l = tr[u].l, r = tr[u].r;
        if (l > R || r < L) return 0;
        if (l >= L && r <= R) return tr[u].sum; // 如果完整命中, 返回现成的

        pushdown(u);
        return query(ls, L, R) + query(rs, L, R);
    }
} T[92]; // A~Z:65+26=91,所以开92

int main() {
#ifndef ONLINE_JUDGE
    freopen("P2787.in", "r", stdin);
#endif
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);

    cin >> n >> m;                                                  // 字母个数，操作次数
    for (int i = 1; i <= n; i++) cin >> a[i], a[i] = toupper(a[i]); // 读入每个字符，并且转成大写

    for (char i = 'A'; i <= 'Z'; i++) T[i].build(1, 1, n); // 创建26个线段树
    for (int i = 1; i <= n; i++) T[a[i]].modify(1, i, i, 1);
    // 枚举字符串中每个字符，两个属性：哪根树，哪个位置，修改为1

    while (m--) {
        int op, l, r;
        char k;
        cin >> op >> l >> r;
        if (op == 1) {
            cin >> k;
            k = toupper(k);
            cout << T[k].query(1, l, r) << endl; // 查询第k棵线段树中[x,y]之间的区间和
        }
        if (op == 2) {
            cin >> k;
            k = toupper(k);
            for (char i = 'A'; i <= 'Z'; i++) // 枚举每棵线段树
                if (i == k)
                    T[i].modify(1, l, r, 1); // 修改的是第i根线段树，区间整体修改为1
                else
                    T[i].modify(1, l, r, 0); // 其它线段树，区间整体修改为0
        }

        if (op == 3) {
            for (char i = 'A'; i <= 'Z'; i++) {
                f[i] = T[i].query(1, l, r); // 将第i棵线段树中[x,y]的区间和保存起来，放到f[i]中
                T[i].modify(1, l, r, 0);    // 放完了就修改为0,表示清除掉懒标记
            }

            // 利用区间修改和桶，完成类似于排序的操作
            for (char i = 'A'; i <= 'Z'; i++)
                if (f[i]) T[i].modify(1, l, l + f[i] - 1, 1), l += f[i];
        }
    }
    return 0;
}
```
### 三、珂朵莉树

> - $ODT$卡$13$个测试点，无法优化解决


一看到区间推倒……推平操作就想到 **珂朵莉树**

区间推平直接$assign$，查询暴力，排序的话开一个桶统计，然后一个字母一个字母加就好了

```cpp {.line-numbers}
// 柯朵莉树，即使吸氧，也过不是最后一个测试点，TLE
#include <bits/stdc++.h>
using namespace std;
const int N = 5e4 + 5;

// 柯朵莉树模板
struct Node {
    int l, r;      // l和r表示这一段的起点和终点
    mutable int v; // v表示这一段上所有元素相同的值是多少,注意关键字 mutable,使得set中结构体属性可修改
    bool operator<(const Node &b) const {
        return l < b.l; // 规定按照每段的左端点排序
    }
};
set<Node> s; // 柯朵莉树的区间集合

// 分裂:[l,x-1],[x,r]
set<Node>::iterator split(int x) {
    auto it = s.lower_bound({x});
    if (it != s.end() && it->l == x) return it; // 一击命中
    it--;                                       // 没有找到就减1个继续找
    if (it->r < x) return s.end();              // 真的没找到,返回s.end()

    int l = it->l, r = it->r, v = it->v; // 没有被返回，说明找到了,记录下来，防止后面删除时被破坏
    s.erase(it);                         // 删除整个区间
    s.insert({l, x - 1, v});             //[l,x-1]拆分
    // insert函数返回pair，其中的first是新插入结点的迭代器
    return s.insert({x, r, v}).first; //[x,r]拆分
}

// 区间加
void add(int l, int r, int v) {
    // 必须先计算itr,后计算itl
    auto R = split(r + 1), L = split(l);
    for (auto it = L; it != R; it++) it->v += v;
}
// 区间赋值
void assign(int l, int r, int v) {
    auto R = split(r + 1), L = split(l);
    s.erase(L, R);       // 删除旧区间
    s.insert({l, r, v}); // 增加新区间
}

// 查询字符k出现的次数
int getcnt(int l, int r, char k) {
    auto R = split(r + 1), L = split(l);
    int res = 0;
    for (; L != R; L++) res += (L->v == k) ? L->r - L->l + 1 : 0; // 暴力统计值为k的个数
    return res;
}

int b[26];                  // 计数用的桶，共26个字符
void px(int l, int r) {     // 将区间[l,r]之间的字符进行排序
    memset(b, 0, sizeof b); // 多次使用，每次使用前清空

    auto R = split(r + 1), L = split(l);
    for (auto it = L; it != R; it++) b[it->v - 'A'] += it->r - it->l + 1; // 用桶来统计计数
    s.erase(L, R);                                                        // 将旧区间删除掉

    int pos = l;
    for (int i = 0; i < 26; i++) // 由小到大枚举每个字符A~Z，然后插入A的数量，B的数量，也就是完成了a~z的排序
        if (b[i]) {
            s.insert({pos, pos + b[i] - 1, i + 'A'});
            pos += b[i];
        }
}
// 学习到cin可以结合char[]进行操作，如果想把下标0的位置让出来，就直接cin>>ch+1
int main() {
#ifndef ONLINE_JUDGE
    freopen("P2787.in", "r", stdin);
#endif
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    int n, m;
    char x;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> x;
        if (x >= 'a') x -= 'a' - 'A'; // 本题输入不区分大小写，所以，输入的小写字母统一换成大写字母
        s.insert({i, i, x});
    }

    char k;
    while (m--) {
        int op, l, r;
        cin >> op >> l >> r;
        if (op != 3) {
            cin >> k;
            if (k >= 'a') k -= 'a' - 'A';
        }

        if (op == 1)
            printf("%d\n", getcnt(l, r, k)); // 查询k出现的次数
        else if (op == 2)
            assign(l, r, k); // 全部替换为k
        else
            px(l, r); // 按照a~z的顺序排序
    }
    return 0;
}
```