python/TangDou/AcWing/ChaFenYueShu/1170.md

## [$AcWing$ $1170$ 排队布局](https://www.acwing.com/problem/content/1172/)

### 一、题目描述
当排队等候喂食时，奶牛喜欢和它们的朋友站得靠近些。

农夫约翰有 $N$ 头奶牛，编号从 $1$ 到 $N$，沿一条直线站着等候喂食。

奶牛排在队伍中的顺序和它们的编号是相同的。

因为奶牛相当苗条，所以可能有两头或者更多奶牛站在同一位置上。

如果我们想象奶牛是站在一条数轴上的话，允许有两头或更多奶牛拥有相同的横坐标。

一些奶牛相互间存有好感，它们希望两者之间的距离 **不超过** 一个给定的数 $L$。

另一方面，一些奶牛相互间非常反感，它们希望两者间的距离 **不小于** 一个给定的数 $D$。

给出 $M_L$ 条关于两头奶牛间有好感的描述，再给出 $M_D$ 条关于两头奶牛间存有反感的描述。

你的工作是：
- ① 如果不存在满足要求的方案，输出$-1$
- ② 如果 $1$ 号奶牛和 $N$ 号奶牛间的距离可以任意大，输出$-2$
- ③ 计算出在满足所有要求的情况下，$1$ 号奶牛和 $N$ 号奶牛间可能的 **最大距离**

**输入格式**
第一行包含三个整数 $N$,$M_L$,$M_D$。

接下来 $M_L$ 行，每行包含三个正整数 $A,B,L$，表示奶牛 $A$ 和奶牛 $B$ **至多** 相隔 $L$ 的距离。

再接下来 $M_D$ 行，每行包含三个正整数 $A,B,D$，表示奶牛 $A$ 和奶牛 $B$ **至少** 相隔 $D$ 的距离。

**输出格式**
输出一个整数，如果不存在满足要求的方案，输出$-1$；如果 $1$ 号奶牛和 $N$ 号奶牛间的距离可以任意大，输出$-2$；否则，输出在满足所有要求的情况下，$1$ 号奶牛和 $N$ 号奶牛间可能的 **最大距离**。

**数据范围**
$2≤N≤1000,1≤M_L,M_D≤10^4,1≤L,D≤10^6$

**输入样例**：
```cpp {.line-numbers}
4 2 1
1 3 10
2 4 20
2 3 3
```

**输出样例**：
```cpp {.line-numbers}
27
```

### 二、题目解析

本题同样是 **差分约束** 的问题，要求$1$到$n$之间可能的 **最大距离**，这道题使我们更加深刻的理解了差分约束的思想。在[$AcWing$ $1169$ 糖果](https://www.acwing.com/problem/content/1171/) 里，仔细的讲解了差分约束的基本思想，以及 **不等式组**
- **求最大解需要求最短路**
- **求最小解需要求最长路**

这里不等式解的最大最小都是相对而言的。比如$a_2 <= a_1 + 1$,$a_3 <= a_2 + 1$，求最短路和最长路的建图如下图所示：

![](https://img-blog.csdnimg.cn/20201023192521343.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzMwMjc3MjM5,size_16,color_FFFFFF,t_70)

- 对于 **最短路** 而言，设起点$a_1 = 0$，求得$a_2$的最大值是$1$，$a_3$的最大值是$2$
- 对于 **最长路** 而言，设起点$a_3 = 0$，求得$a_2$的最小值是$-1$，$a_1$的最小值是$-2$
所以所谓的最值都是相对的，本题求$1$到$n$之间的 **最大距离** 很能够体现这种相对的关系。

下面梳理下 **已知的结论**：
- ① 对于同一个不等式组，最短路和最长路建图是完全不同的，边的大小互为相反数，方向相反
- ② 如果不等式组无解，即没有合法的一组解使得所有的不等式都成立，那么 **建立的最短路图中一定存在负环，建立的最长路的图中一定存在正环**。
- ③ 如果不等式组有解，**最短路求得的是最大解，最长路求得的是最小解**。

要求$1$到$n$之间的距离，不妨设$1$号点的坐标就是$0$，从$0$出发到达终点$n$，要想距离最大，则$n$号点的解就要最大，所以需要求 **最短路**。
> 当然如果将$n$的坐标设置为$0$，也可以通过求最长路来使得$1$到$n$之间的距离最大。
> **疑**:这句话我没有理解上去，不明白为什么

本题的约束条件有三个，
#### $a_{i-1} <= a_i$
> **解释**：农夫约翰有 $N$ 头奶牛，编号从 $1$ 到 $N$，沿一条直线站着等候喂食。
 
#### $a_i - a_j <= L$
> **解释**:两者之间的距离 **不超过** 一个给定的数 $L$。

#### $a_i - a_j >= D$
> **解释**:两者间的距离 **不小于** 一个给定的数 $D$。

暂且不去分析具体的约束条件，先讨论一个问题，**什么情况下起点到终点的距离可以无限大**。关于这个问题，很多博客仅仅给出了必要条件，比如说从起点到达不了终点，图中的两点间没有可达的路径，没有约束距离就无限大，但这仅仅是必要条件而非充分条件。比如下面的不等式组：

$$
\large \left\{\begin{matrix}
a_1 <= a_2 - 1 & \\ 
a_2 <= a_3 - 1 & 
\end{matrix}\right.
$$

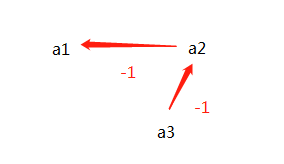
最短路建图如下：

![](https://img-blog.csdnimg.cn/20201023194218359.png)

从$a_3$是可以到达$a_1$的，图中没有孤立的点，$a_3 = 0$时，$a_1$就可以无限小，他们的距离就无限大。这个简单的例子可以看出，**差分约束的不等式组对应的图如果没有环，起点和终点的距离是可以无限大的**。

要想两点间距离有限，**需要图中有一个适当的环**，来约束解的范围。上图的不等式组可以推出$a_1 <= a_3 - 2$，那么我再加上一个不等式约束$a_1 >= a_3 - 4$,，就成功的将$a_1$到$a_3$之间的距离限制在$4$个单位以内了。对应图中的表现不过是$a_1$到$a_3$连一条边权为$4$的边，我们分析此时环的长度$4 - 1 - 1 = 2$是大于$0$的。所以我们可以得出下面的结论：

- ① **最短路的图中如果存在负环，差分约束问题无合法解**
- ② **最短路的图中如果存在正环，正环上任意两点间的距离都是有限的**
- ③ **最短路的图中不存在环,图中任意两点间的距离都可以是无限大的**

> 这个结论可以类比到最长路的图中。

**换一种表达形式的话就是如果要图中的两点间距离有限，需要存在正环，且这两个点都在环上。**

那么本题我们是否需要判断了负环还要判断正环呢？实际上是不需要的。

第一个约束条件$a_i >= a_{i-1}$，构建的最短路图中$a_n$可以到达$a_{n-1}$,$a_{n-1}$可以到达$a_{n-2}$,...。所以$a_n$可以到达每一点，包括$a_1$。我们先以$a_n$为起点，求一遍最短路，如果存在负环，则不等式组无解，如果不存在负环，那么不等式组肯定有解，下面要判断的就是$a_n - a_1$的结果是否可以无限大。在确定了不等式组有解的情况下，我们以$a_1$为起点再求一遍最短路，当然$a_1$不一定能够到达每一点，如果$a_1$到达不了$a_n$，说明不存在一个环，环上同时包含$a_1$到$a_n$。如果$a_1$出发可以到达$a_n$，则一定存在由$a_1、a_n$构成的正环。从$a_1$出发可以到达$a_n$，$a_n$出发可以到达$a_1$，这个条件保证了环的存在。第一次以$a_n$为起点求最短路时不存在负环，说明这个环一定不是负环，那么就是正环了（即使环的长度为$0$也是有解的）。根据我们上一段推出的结论可知，此时$a_1$和$a_n$之间的距离是有限的，并且第二次求最短路过程中$a_1$是起点，求得的$a_n$是最大值，所以此时的$a_n$就是我们要求的最大距离了。

**最后再总结下本题给我们的经验**:
- ① 最短路存在负环，差分约束问题无解
- ② 最短路存在正环，环上任意两点之间距离有限
- ③ 最短路不存在环，任意两点间距离可以是无穷大
---
- ④ 最长路存在正环，差分约束问题无解
- ⑤ 最长路存在负环，环上任意两点之间距离有限
- ⑥ 最长路不存在环，任意两点间距离可以是无穷大

### 三、实现代码
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;

const int N = 1010, M = 20010, INF = 0x3f3f3f3f;

int n, m1, m2;

int dist[N], cnt[N];
bool st[N];

int h[N], w[M], e[M], ne[M], idx;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

bool spfa(int sz) {
    // spfa要调用2次，所以每次调用要清空一下st,cnt,dist
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);
    memset(dist, 0x3f, sizeof dist); // 最短路，初始化为正无穷
    queue<int> q;

    // 前sz个节点入队列
    for (int i = 1; i <= sz; i++) {
        dist[i] = 0;
        q.push(i);
        st[i] = true;
    }

    while (q.size()) {
        int u = q.front();
        q.pop();
        st[u] = false;

        for (int i = h[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (dist[v] > dist[u] + w[i]) { // 最短路
                dist[v] = dist[u] + w[i];
                cnt[v] = cnt[u] + 1;
                if (cnt[v] >= n) return true; // 判负环
                if (!st[v]) {
                    q.push(v);
                    st[v] = true;
                }
            }
        }
    }
    return false;
}

int main() {
    scanf("%d%d%d", &n, &m1, &m2);
    memset(h, -1, sizeof h);

    while (m1--) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        // 表示奶牛 A 和奶牛 B 至多相隔 L 的距离。
        // b-a <=c  ==> b < a + c
        add(a, b, c);
    }

    while (m2--) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        // 表示奶牛 A 和奶牛 B 至少相隔 D 的距离。
        //  b - a >=c => a <= b - c
        add(b, a, -c);
    }

    // 奶牛排在队伍中的顺序和它们的编号是相同的
    for (int i = 1; i < n; i++) add(i + 1, i, 0); // x_{i+1} - x_i >= 0  => x_i <= x_{i+1}

    if (spfa(n))
        puts("-1"); // 从n出发找一下负环,如果负环存在则无解
    else {
        spfa(1); // 如果从1号节点出发，可以成功走到n号节点，则 dist[n]就不会是INF,如果是INF就说明没有走到过 n点。表示在不等式组中不存在 x_n,x_1之间的传递关联关系，即x_n可以随意
        if (dist[n] == INF)
            puts("-2");
        else
            printf("%d\n", dist[n]);
    }
    return 0;
}
```