python/TangDou/AcWing/BIT/LOJ10115.md

## [$LOJ \ 10115$. 「一本通 4.1 例 3」校门外的树](https://loj.ac/p/10115)

### 一、题目描述
校门外有很多树，学校决定在某个时刻在某一段种上一种树，保证任一时刻不会出现两段相同种类的树，现有两种操作：

- $K=1$，读入 $l,r$ 表示在 $l$ 到 $r$ 之间种上一种树，每次操作种的树的种类都不同；
- $K=2$，读入 $l,r$ 表示询问 $l$ 到 $r$ 之间有多少种树。
注意：每个位置都可以重复种树。

**输入格式**
第一行 $n,m$ 表示道路总长为 $n$，共有 $m$ 个操作；
接下来 $m$ 行为 $m$ 个操作。

**输出格式**
对于每个 $k=2$ 输出一个答案。


### 二、题目解析

开始怎么想都不知道怎么维护不同段中树的种类是否相同的情况，感觉这题有个思维技巧还是挺难想的，就是我们要开两个数组，$sum_1$分别维护左端点的数目，另一个数组$sum_2$维护右端点的数目。这样区间$[l,r]$的树的种类的数目就是$1-r$中左端点的数目减去$1-(l-1)$中右端点的数目，即表示为$sum_1[r]-sum_2[l-1]$。

![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/{year}/{month}/{md5}.{extName}/202308150818883.png)

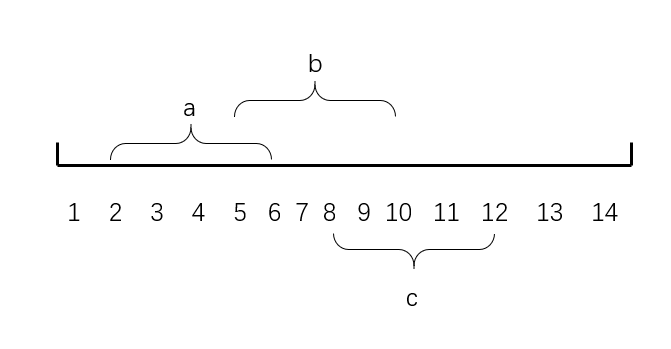
如图假如我们第一次在区间$a[2,6]$种上一种树，然后再在区间$b[5,10]$种上一种树，这时我们要统计区间$c[8,12]$中树的种类数目，我们就统计$[1,12]$中左端点的数目即 $sum_1[12]$等于$2$，说明有两种树可能在给定区间内，然后我们再求区间$[1,7]$中右端点的数目即$sum_2[7]=1$,表示有一种树完全在给定区间左边，并不是我们要求的，所以减去就好了，所以答案就为$sum_1[12]-sum_2[7]$了。

### $Code$
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
int const N = 50010;
int n, m;
// 树状数组模板
int c1[N], c2[N];

#define lowbit(x) (x & -x)
typedef long long LL;

void add(int c[], int x, int v) {
    while (x < N) c[x] += v, x += lowbit(x);
}

LL sum(int c[], int x) {
    LL res = 0;
    while (x) res += c[x], x -= lowbit(x);
    return res;
}
int main() {
#ifndef ONLINE_JUDGE
    freopen("LOJ10115.in", "r", stdin);
#endif
    int k, l, r;
    scanf("%d%d", &n, &m); // 第一行 n,m 表示道路总长为 n，共有 m 个操作；
    // n下面没有使用过。为什么呢？其实是n的上限N有用！我们就没有用到n,代码模板中也去掉了n的

    for (int i = 1; i <= m; i++) {
        scanf("%d%d%d", &k, &l, &r);
        if (k == 1)
            add(c1, l, 1), add(c2, r, 1); // c1记录左括号的个数，c2记录右括号的个数
        else
            printf("%d\n", sum(c1, r) - sum(c2, l - 1));
    }
    return 0;
}
```

### 三、线段树解法
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
int const N = 50010;
int n, m;

// 线段树+单点修改
#define mid ((l + r) >> 1)
#define ls (u << 1)
#define rs (u << 1 | 1)
struct Node {
    int l, r;
    int sum;
} tr[2][N << 2];

void pushup(int w, int u) {
    tr[w][u].sum = tr[w][ls].sum + tr[w][rs].sum;
}
void build(int w, int u, int l, int r) {
    tr[w][u].l = l, tr[w][u].r = r;
    if (l == r) return;
    build(w, ls, l, mid);
    build(w, rs, mid + 1, r);
}

void change(int w, int u, int x, int v) {
    int l = tr[w][u].l, r = tr[w][u].r;
    if (l == r) {
        tr[w][u].sum += v;
        return;
    }
    if (x <= mid)
        change(w, ls, x, v);
    else
        change(w, rs, x, v);
    pushup(w, u);
}

int query(int w, int u, int L, int R) {
    int l = tr[w][u].l, r = tr[w][u].r;
    if (l >= L && r <= R) return tr[w][u].sum;
    if (l > R || r < L) return 0;
    return query(w, ls, L, R) + query(w, rs, L, R);
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("LOJ10115.in", "r", stdin);
#endif
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    int op, l, r;
    cin >> n >> m; // 第一行 n,m 表示道路总长为 n，共有 m 个操作；
    // n下面没有使用过。为什么呢？其实是n的上限N有用！我们就没有用到n,代码模板中也去掉了n的
    build(0, 1, 1, n);
    build(1, 1, 1, n);

    while (m--) {
        cin >> op >> l >> r;
        if (op == 1)
            change(0, 1, l, 1), change(1, 1, r, 1);
        else
            printf("%d\n", query(0, 1, 1, r) - query(1, 1, 1, l - 1));
    }
    return 0;
}
```