python/TangDou/Topic/前缀和和差分洛谷题单总结.md

## 前缀和和差分洛谷题单总结

[参考文献](https://blog.csdn.net/piqihaoshaonian/article/details/127515000)

### 一、公式
#### 前缀和的公式
一维：$s[i] = a[i] + s[i-1]$

二维：$s[i][j] = a[i][j] + s[i-1] [j] + s[ i] [j-1] - s[i-1][j-1]$

#### 差分的公式
一维：$b[i] =s[i] - s[i-1]$

二维：$b[i] = s[i][j] - s[i-1][j]-s[i][j-1]+s[i-1][j-1]$

### 二、题单
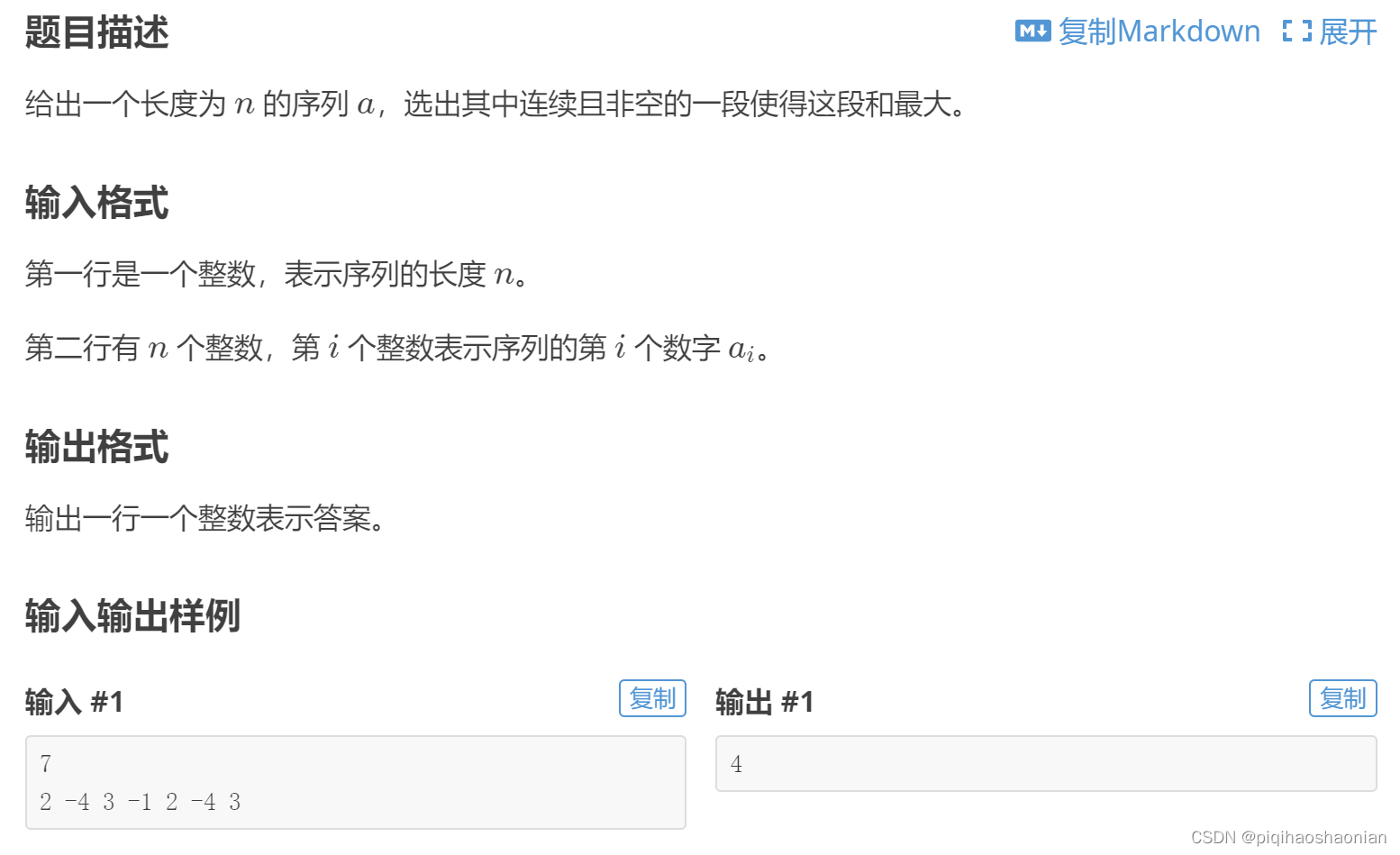
#### [$P1115$ 最大子段和](https://www.luogu.com.cn/problem/P1115)
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170827397.png)

**分析**
先求每个位置的前缀和（某个区间求和前缀和可以说是最快的），然后去找该位置前前缀和的最小值，如果要求一段和最大，就要用这段和减去前面最小的值。

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
const int INF = 0x3f3f3f3f;
int n, a[N], s[N], ans[N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i], s[i] = s[i - 1] + a[i]; // 前缀和

    int mi = 0;
    for (int i = 1; i <= n; i++) {
        ans[i] = s[i] - mi;
        mi = min(mi, s[i]);
    }
    int res = -INF;
    for (int i = 1; i <= n; i++) res = max(res, ans[i]);
    cout << res << endl;
    return 0;
}
```

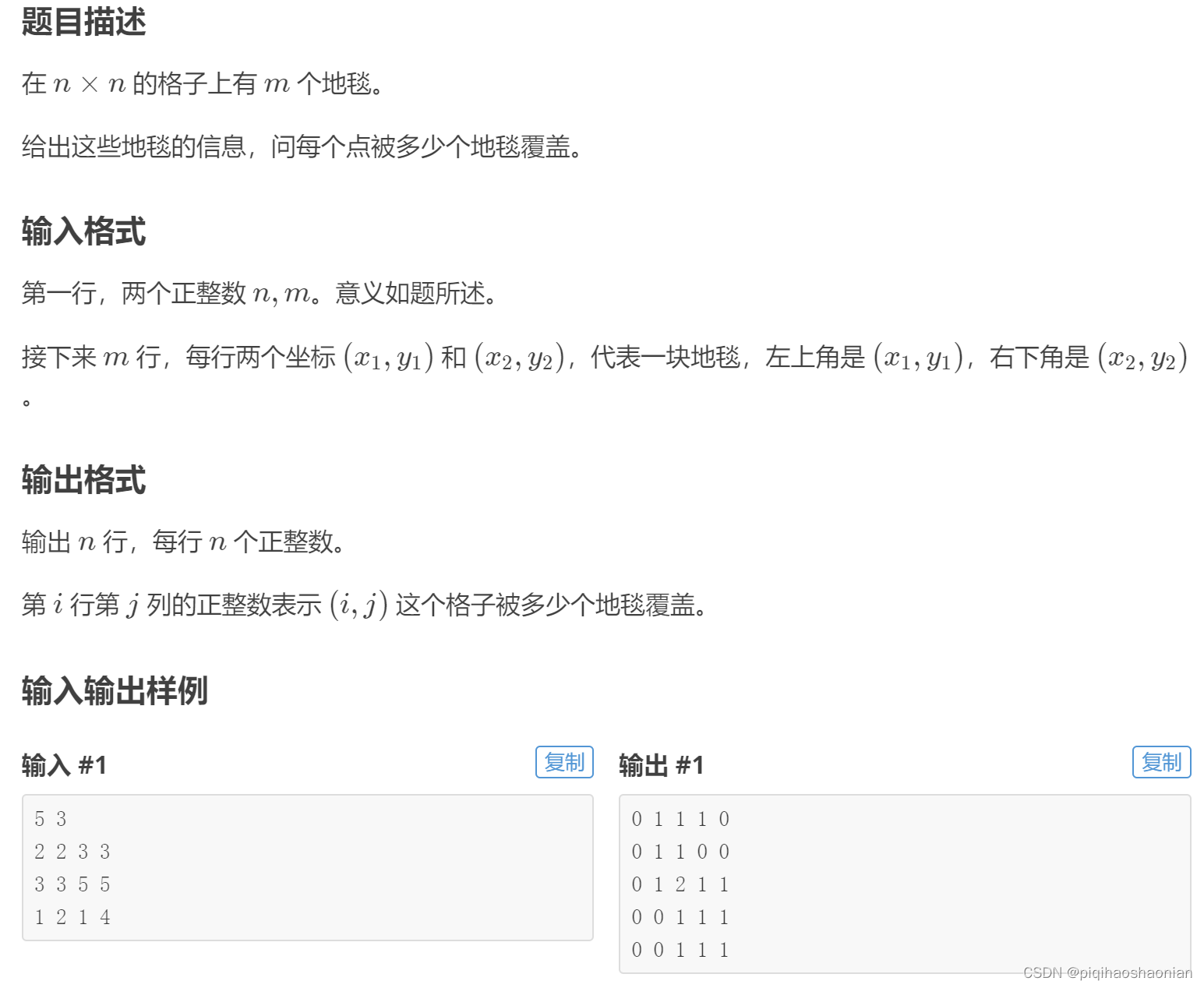
#### [$P3397$ 地毯](https://www.luogu.com.cn/problem/P3397)
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170847131.png)

**分析**
看到这里的时候，我就想到了一个矩阵的某个子矩阵进行加减，瞬间想到二维差分和二位前缀和,二位差分的公式为：

![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170848375.png)

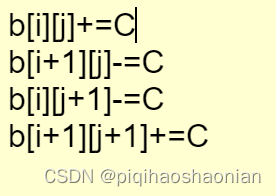
由差分算的二位前缀和公式：
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170849629.png)

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;

const int N = 1010;
int b[N][N], s[N][N];
int n, m;

int main() {
    cin >> n >> m;
    while (m--) {
        // 从0开始构建差分数组
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        b[x1][y1] += 1; // 进行子矩阵的加减，差分
        b[x2 + 1][y1] -= 1;
        b[x1][y2 + 1] -= 1;
        b[x2 + 1][y2 + 1] += 1;
    }
    // 还原为原始数组
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            s[i][j] = b[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1]; // 把之前的加减结果进行求和
            printf("%d ", s[i][j]);                                          // 注意输出格式，每个数带一个空格
        }
        printf("\n"); // 结束一行的输出输出一个换行符号
    }
    return 0;
}
```
### [$P1083$ [$NOIP2012$ 提高组] 借教室](https://www.luogu.com.cn/problem/P1083)
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170927931.png)

#### 暴力
还是先看暴力怎么做吧，对于$m$次借教室，我们可以每次把区间$s\sim t$的空教室数$r-=d$，当有一次$r<0$时，则当前这个人无法被满足，直接输出$-1$和当前这个人的号数，然后直接结束程序。如果$m$次借教室都操作完成后依然没有房间数$r<0$，则说明所有人都可以被满足，则输出$0$。

综合上述做法，得分$60$。

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
int n, m;
const int N = 1000010;
int r[N];
int main() {
    cin >> n >> m;
    // 每一天可租借教室数
    for (int i = 1; i <= n; i++) cin >> r[i];

    // 从哪天到哪天，借多少个
    for (int i = 1; i <= m; i++) {
        int d, s, t;
        cin >> d >> s >> t;
        // 从开始天到结束天
        for (int j = s; j <= t; j++) {
            r[j] -= d;      // 减去借走的教室数
            if (r[j] < 0) { // 小于0了！
                cout << -1 << endl
                     << i << endl;
                return 0;
            }
        }
    }

    cout << 0 << endl;
    return 0;
}
```
显然，这样做法的时间复杂度时$O(N*M)$的，无法通过此题，从而我们可以推知该题正确的时间复杂度应该是$log$级的。

#### 正解
既然时间复杂度时$log$级的，于是想到了二分。

再看到每个人借教室的时间可以看成一个区间，且该区间只会对其他在该区间要借教室的人产生影响，对于区间之外的借教室的人是不会产生影响的，于是又想到了差分。

差分序列：（可用于区间增减）记录相邻两个量的变化量，所以当在一段区间$[l,r]$上增加$a$时，只需要在$l$处加$a$，在$r+1$处$-a$即可。

对于为什么可以二分：如果一个人无法被满足，则他后面的人全都不能被满足；如果一个人可以被满足，则他前面的人都可以被满足,这恰恰吻合了我们二分的性质。

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;
#define int long long
#define endl "\n"
int n, m;                   // 天数和订单的数量
int r[N];                   // 第i天学校有r[i]个教室可借用
int d[N], s[N], t[N];       // 借的教室数目、从第s天借到t天
int b[N];                   // 差分数组
bool check(int x) {         // 判断能不能通过x个人
    memset(b, 0, sizeof b); // 每次判断都要先初始化差分数组
    int sum = 0;            // 记录需要借的教室数
    for (int i = 1; i <= x; i++) {
        b[s[i]] += d[i];     // 因为只会对在s~l之间要借用教室的人产生影响，所以可以差分
        b[t[i] + 1] -= d[i]; // 差分,注意:是t[i]+1，因为要包含t[i]这个点
    }
    for (int i = 1; i <= n; i++) {
        sum += b[i];                  // 因为cf是差分数组，所以sum就是在第i天的借教室的总数
        if (sum > r[i]) return false; // 不可行，如果要借的教室多于空的教室
    }
    return true; // 可行
}
signed main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> r[i];
    for (int i = 1; i <= m; i++) cin >> d[i] >> s[i] >> t[i];
    if (check(m)) {        // 如果全部满足
        cout << 0 << endl; // 输出0
        exit(0);           // 直接结束程序
    }
    int l = 1, r = m; // 二分左右区间
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid))  // 如果可行
            l = mid + 1; // 增多满足人数
        else             // 否则
            r = mid;     // 减少满足人数
    }
    cout << "-1" << endl
         << l; // 输出-1和需要修改的人
}
```

### [$P3406$ 海底高铁](https://www.luogu.com.cn/problem/P3406)
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202312170857701.png)

**分析**
① 每一段的最小费用加起来则总体费用最小。

② 这里的区间是线段而不是一个具体的数，所以我们需要以一个统一的标准进行区间段的区分：于是我们想到了以每个区间的左端点值进行整个线段的记录。

③ 节约时间可以对某段区间做同样的加减数的方法：想到的就是差分（当然有差分就会有由差分求前缀和）。

④ 最后用得到的线段数比较两种购买方案。


**注意**
当然代码中还有很多需要记录的细节！！！例如：线段数是站点数-1，同时差分和前缀和的循环最好是从1开始（涉及边界问题）