python/TangDou/Topic/【Floyd专题】.md

## 图论-多源最短路径（$Floyd$算法）

### 一、$Floyd$
$Floyd$算法是一次性求所有结点之间的最短距离，能处理负权边的图，程序比暴力的$DFS$更简单，但是复杂度是$O(n^3)$，只适合 $n < 200$的情况。
$Floyd$运用了 **动态规划** 的思想，求 $i 、 j$两点的最短距离，可分两种情况考虑，即经过图中某个点 $k$的路径和不经过点 $k$ 的路径，**取两者中的最短路径**。


- 判断负圈
眼尖的人儿可能发现邻接矩阵 $mp$ 中， $mp[i][i]$并没有赋初值$0$，而是 $inf$。并且计算后 $mp[i][i]$的值也不是 $0$，而是 $mp[i][i]=mp[i][u]+……+mp[v][i]$，即从外面绕一圈回来的最短路径，而这正 **用于判断负圈**，即 $mp[i][i]<0$。

相关变形结合题目讲，如：负圈、打印路径、最小环、传递闭包

记录坑点：**重复边**，保留最小的那个。


### 二、模板
```cpp {.line-numbers}
void floyd() {
	for (int k = 1; k <= n; k++)
		for (int i = 1; i <= n; i++)
			if (g[i][k] != inf)  //优化
				for (int j = 1; j <= n; j++)
					if (g[i][j] > g[i][k] + g[k][j])
						g[i][j] = g[i][k] + g[k][j];
}
```

### 三、判负环

#### [$POJ-3259$ $Wormholes$](https://link.juejin.cn/?target=https%3A%2F%2Fvjudge.net%2Fproblem%2FPOJ-3259)

**类型**
判负环

**题意**
- 正常路是$m$条双向正权边 
- 虫洞是$w$条单向负权边 
- 题目让判断是否有负权回路

**办法**
利用$Floyd$找两点间花费的最短时间，判断从起始位置到起始位置的最短时间是否为负值（判断负权环），若为负值，说明他通过虫洞回到起始位置时比自己最初离开起始位置的时间早。

**代码实现**:
在第二重循环，求完第$i$个结点后判断。$i$到$i$之间的最短距离是一个负值，说明存在一个经过它的负环。

```cpp {.line-numbers}
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int INF = 0x3f3f3f3f;

const int N = 502;
int n, m, w;
int g[N][N];

// floyd判断是否存在负圈
bool floyd() {
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            if (g[i][k] != INF) { // 优化
                for (int j = 1; j <= n; j++)
                    if (g[i][j] > g[i][k] + g[k][j])
                        g[i][j] = g[i][k] + g[k][j];
                if (g[i][i] < 0) return true; // 发现负圈
            }
    return false;
}
int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> n >> m >> w;
        memset(g, INF, sizeof g); // 初始化邻接矩阵

        // 双向正值边
        while (m--) {
            int a, b, c;
            cin >> a >> b >> c;
            // 注意坑：重边
            g[a][b] = g[b][a] = min(c, g[a][b]);
        }
        // 单向负值边
        while (w--) {
            int a, b, c;
            cin >> a >> b >> c;
            g[a][b] = -c; // 负值边
        }

        if (floyd())
            puts("YES");
        else
            puts("NO");
    }
    return 0;
}
```

### 四、记录最短路径并输出

$floyd$ 算法求最短路（边权可为负）很优美，四行代码就搞定了。今天做了一个题，可以用 $floyd$ 做，但是要最短路的路径。在网上搜了一阵，代码倒是有，但是没有解释，为何是这样的？于是，手推了一遍，写了这篇博客。

不像 $dijkstra$ 和 $spfa$，是一个点一个点加进去的，直接 $pre$ 数组往前倒，倒至起点就行了。$floyd$ 是基于动态规划，这怎么记录路径呢？

开一个 $path$数组，$path[i][j]$ 表示：更新从 $i$ 到 $j$ 的最短路径时，经过的一个中转点。

```cpp {.line-numbers}
void floyd() {
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (dis[i][j] > dis[i][k] + dis[k][j]) {
                    dis[i][j] = dis[i][k] + dis[k][j];
                    path[i][j] = k; //记录i->j是通过k转移的
                }
}
```
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401050754691.png)

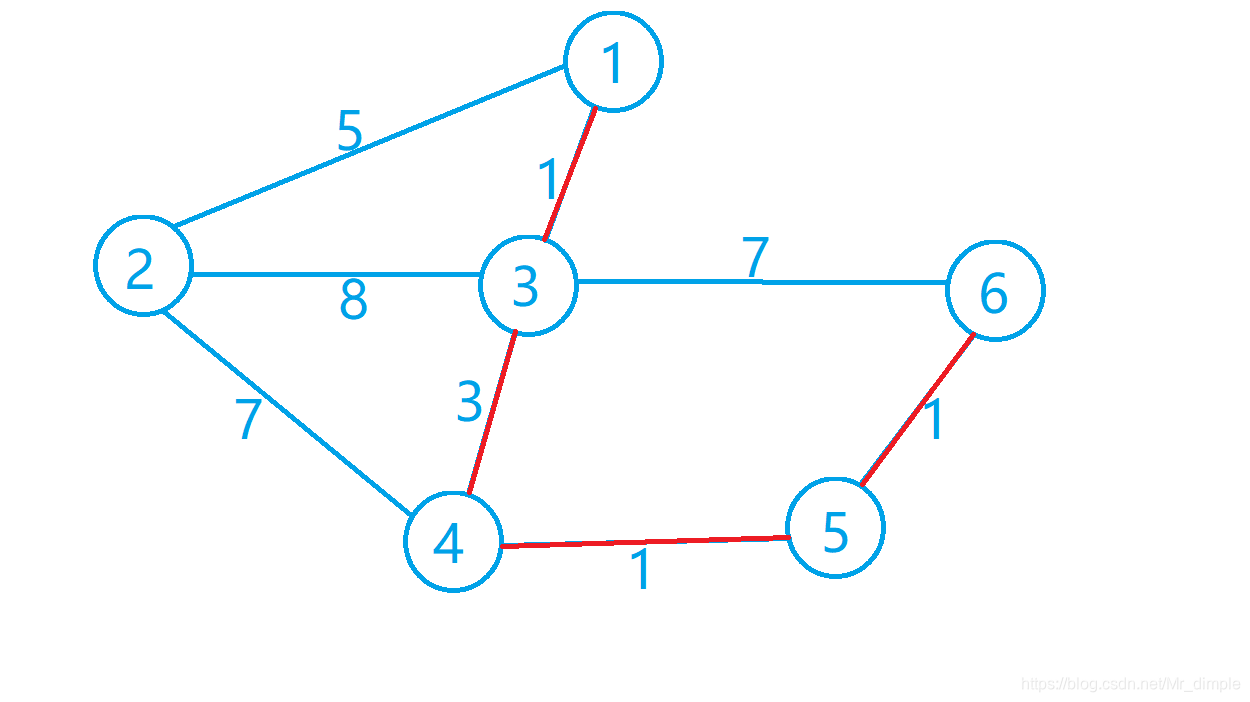
在这个图中，很容易看出，从 $1$ 到 $6$ 之间的最短路径是标红的那几条边。

二重循环所有点，输出 $path$ 数组：
```cpp {.line-numbers}
0 0 0 3 4 5
0 0 0 0 4 5
0 0 0 0 4 5
0 0 0 0 0 5
0 0 0 0 0 0
0 0 0 0 0 0
```
可以看出，$path[1][6]$ 是 $5$，$path[1][5]$ 是 $4$，$path[1][4]$ 是 $3$。那么，最终 $path[i][j]$ 中存的就是 **从$i$到$j$的最短路径中的靠近$j$的最后一个点**。

而我们最终输出路径的思路就是，不断分段最短路径！ 最后输出所有的点。
> **原理：由 $i$ 到 $j$ 的最短路径中的一点 $k$，将最短路径分段为从 $i$ 到 $k$ 的最短路径 和 从 $k$ 到 $j$ 的最短路径，最短路径就为从$i$到$k$的最短路径+从$k$到$j$的最短路径，一直分段，直到分到 $i$ 和 $j$ 为同一点，停止**

可能现在你有些迷糊，我们直接看代码吧！

```cpp {.line-numbers}
void print(int i, int j) { // path[i][j]:从i到j最短路径中经过的一点k
    if (i == j) return;    // 分段到同一点，递归结束
    if (path[i][j] == 0)   // i和j直接相连，就是i到j最短路径不经过任何点
        cout << i << " " << j << endl; 
    else {
        print(i, path[i][j]); // 分段输出从i到k的最短路径
        // 输出从i到k最短路径中的所有点（一定都在从i到j的最短路径中）
        print(path[i][j], j); // 分段输出从k到j的最短路径
        // 输出从j到k最短路径中的所有的点
    }
}
```
就是一个 **递归** 的过程。

我们用上面的图模拟一下：
首先，从 $1$ 到 $6$ 的最短路径，$path[1][6]$中存的是：该最短路径中的最后一个节点 $5$，即，$k = 5$。

那么，递归（分段） 到，从 $1$到$5$的最短路 和 从$5$到$6$的最短路。
- 从$1$到$5$的最短路，$path[1][5]=4$，则又分段为从$1$到$4$的最短路和从$4$到$5$的最短路。
- 从$1$到$4$的最短路，$path[1][4]=3$，则又分段为从$1$到$3$的最短路和从$3$到$4$的最短路。
- $path[1][3]=0$！如图，$1$和$3$直接相连！那么$1$和$3$都是最短路中的点，输出就行了！

**回溯**：
- 从$3$到$4$的最短路，$path[3][4]=0$！$3$和$4$直接相连，$3$和$4$都是最短路中的点，输出！
- 从$4$到$5$的最短路，$path[4][5]=0$！$4$和$5$直接相连，$4$和$5$都是最短路中的点，输出！
- 从$5$到$6$的最短路，$path[5][6]=0$！$5$和$6$直接相连，$5$和$6$都是最短路中的点，输出！

所以，最终输出的就是：
```cpp {.line-numbers}
1 3
3 4
4 5
5 6
```
依次连接就是从$1$到$6$的最短路径了！

**总体代码**
```cpp {.line-numbers}
void floyd() {
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (dis[i][j] > dis[i][k] + dis[k][j]) {
                    dis[i][j] = dis[i][k] + dis[k][j];
                    path[i][j] = k;
                }
}
void print(int i, int j) {
    if (i == j) return;
    if (path[i][j] == 0)
        cout << i << " " << j << endl;
    else {
        print(i, path[i][j]);
        print(path[i][j], j);
    }
}

int main() {
    ··· //一顿初始化，输入数据

    floyd();
    print(1, n); // 输出从1到n的最短路径中的所有点（边）

    return 0;
}

```
**练习题**：



#### [$HDU-1385$ $Minimum$ $Transport$ $Cost$](http://acm.hdu.edu.cn/showproblem.php?pid=1385)

**类型**
打印路径

**题意**
给你所有城市到其他城市的道路成本和经过每个城市的城市税，给你很多组城市，要求你找出每组城市间的最低运输成本并且输出路径，**如果有多条路径则输出字典序最小的那条路径**。 **注意**，起点城市和终点城市不需要收城市税(中间点才收税,也就是插值的$k$收税)。

**分析**
输出路径，多个答案则输出字典序最小的，无法到达输出$-1$。
读入邻接表， $w[]$记录每个城市额外费用， $path[][]$记录路径，$floyd()$里维护即可。然后处理下输出(比较恶心)。

> **解释**：`int path[N][N]; `
$i \rightarrow j$ 可能存在多条路线，我要找最短的。如果有多条最短的，我要字典序最小的。现在路线唯一了吧！比如这条路线最终是
$i \rightarrow a \rightarrow b \rightarrow c \rightarrow d \rightarrow j$,则$path[i][j]=a$,也就是第一个后继节点。

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;

const int N = 1003;
int g[N][N];    // 邻接矩阵
int n;          // n个点
int w[N];       // 额外费用
int path[N][N]; // i->j 可能存在多条路线，我要找最短的。如果有多条最短的，我要字典序最小的。现在路线唯一了吧！比如这条路线最终是
// i->a->b->c->d->j,则path[i][j]=a,也就是第一个后继节点。
void floyd() {
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            if (g[i][k] != INF) // floyd优化
                for (int j = 1; j <= n; j++) {
                    if (g[i][j] > g[i][k] + g[k][j] + w[k]) { // w[k]:点权
                        g[i][j] = g[i][k] + g[k][j] + w[k];   // k的加入，使得i->j的路径变短
                        path[i][j] = path[i][k];              // 如果i->k->j使得i->j更近，那么根据定义path[i][j]就是这条最短路径中距离i最近的那个点，而这个点由于是出现在i->k的必经之路上，而且是i->k的首席弟子，所以，也必然是i->j的首席弟子。
                    }
                    // 处理字典序
                    if (g[i][j] == g[i][k] + g[k][j] + w[k]) {                // 如果存在多条最短路径，也就是，除了k还有其它k1,k2使得i->j距离一样小
                        if (path[i][j] > path[i][k]) path[i][j] = path[i][k]; // 字典序，谁更小就留下谁
                    }
                }
}
int main() {
    while (cin >> n && n) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                path[i][j] = j;                   // 路径初始化,记录整条路径上，离i节点最近的，最短路径上的下一个点，只有i->j时，下一个点可不就是j
                cin >> g[i][j];                   // 不管是不是有边，都先录进来
                if (g[i][j] == -1) g[i][j] = INF; // 如果题目中给出的是无边，那么设置为正无穷。此时，有些记录的path[i][j]就是没用的，但没事，后面会被其它代码替换掉path[i][j]。
            }
        }
        for (int i = 1; i <= n; i++) cin >> w[i]; // 读入点权

        // 多源最短路径
        floyd();

        // 处理询问
        int x, y;
        while (cin >> x >> y) {
            if (x == -1 && y == -1) break;
            printf("From %d to %d :\n", x, y);
            printf("Path: %d", x);
            int u = x, v = y;
            // 理解路径思路:
            // (1) 从起点x出发,用循环打印路径,最后一个打印的肯定是y
            // (2) 从起点x出发,第二个点应该是离x最近的，并且是最短路径上的那个点,这个点就是path[x][y]!
            // path[x][y]：从起点x出发，到终点y有多条最短路径，我们选择字典序最小的那条最短路径，然后path[x][y]就是从x出发，离x最近的这条最短路径上的点。
            while (x != y) {
                printf("-->%d", path[x][y]); // 输出距离x最近的那个点
                x = path[x][y];              // 更换x概念，向y逼近，让循环跑起来
            }

            puts("");
            if (g[u][v] < INF)
                printf("Total cost : %d\n", g[u][v]);
            else
                puts("-1");
            puts("");
        }
    }
    return 0;
}
```
**$TODO$**
据说可以使用$Dijkstra$算法解决，有空可以试试: **[链接](https://blog.csdn.net/K_R_forever/article/details/80525757)**



https://juejin.cn/post/6935691567696969764