huanghai
/
python
1
0
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity
You can not select more than 25 topics Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
Branches Tags
${ item.name }
Create tag ${ searchTerm }
Create branch ${ searchTerm }
from 'main'
${ noResults }
python/TangDou/Topic/鸽巢原理.md

463 lines
18 KiB
Raw Permalink Normal View History Unescape

'commit'
2 years ago
## 抽屉原理,鸽巢原理
### 一、鸽巢原理
别名：鸽笼原理。狄利克雷抽屉原理。
最简单的一种形式：有$m + 1$只鸽子，$m$个笼子，那么至少有一个笼子有至少两只鸽子。当然，换个角度来说：有$m − 1$只鸽子，$m$个笼子，那么至少有一个笼子是空的。
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202311240947996.png)
**初级加强**：有$m$个笼子，$k ∗ m + 1$只鸽子，那么至少有一个笼子有至少$k+1$只鸽子。
**高级加强**：
设$q_1,q_2,...,q_n$是正整数，如果有：
$$S_2=q_1+q_2+...+q_n-n+1$$
只鸽子需要放进$n$个笼子，那么或者第一个笼子至少有$q_1$只鸽子，或者第二个笼子至少有$q_2$只鸽子，...,或者第$q_n$个鸽笼至少有$q_n$只鸽子。
**反证法**
假设每个笼子里的鸽子数量都比题目要求的目标结果少一只：
即第 $i$ 个笼中最多有 $q_i−1$ 只鸽子，那么总共最多有：
$$S_1=(q_1−1)+(q_2−1)+⋯+(q_n−1)=q_1+q_2+⋯+q_n−n$$
此时发现$S_2=S_1+1$,也就是还有一只鸽子没有笼子，因此矛盾，所以假设错误，至少有一个笼子$i$,满足有$q_i$只鸽子。
### 二、 简单应用
（1）从一副纸牌（排除大小王）中随机抽取 $5$ 张纸牌，则至少存在两张牌的花色一致。
>**注意**:此时的 **鸽** 与 **笼** 分别指什么？
**鸽**：$5$ 张纸牌的各自花色，**笼**：$4$种花色；
（2）三个人分四块蛋糕，本着公平的原则，一定有一个人会分得 $2$ 块蛋糕；
（3）五个蛋糕要放在两个盒子里，则存在一个盒子存放的蛋糕数量至少为$3$.
$(5−1)2+1$（$5-1$：表示减去余出来的一个鸽子）
### 三、高级加强
任意给 $m$ 个整数$a_1,a_2,a_3,...,a_m$。
**求证**：必存在整数 $s,t(0≤s＜t≤m)$,使得 $m$ 整除 $a_{s+1}+a_{s+2}+…+a_t$。
> **解释**:就是在序列$a_1，a_2，……，a_m$中存在连续的$a_x$，使得这些$a$的和能够被$m$整除。
**证明**：
考虑$m$个和
$$\large a_1,a_1+a_2,a_1+a_2+a_3,……,a_1+a_2+a_3+...+a_m$$
如果这些和当中的 **任意一个可被$m$整除**，那么结论就成立。
那如果没有任意一个可以被$m$整除呢？
假设这些和中的每一个除以$m$都有一个非零余数，余数等于$1,2，……，m-1$ 中的一个数。因为有$m$个和，而只有$m-1$个余数，所以必然有两个和除以$m$有相同的余数。因此，存在整数 $s$和 $t$，$s<t$，使得$a_1+a_2+...+a_s$ 和 $a_1+a_2+...+a_t$除以$m$有相同的余数$r$：
$$
\large \left\{\begin{matrix}
a_1+a_2+...+a_s=b*m+r & \\
a_1+a_2+...+a_t=c*m+r &
\end{matrix}\right.
$$
二式相减，发现$a_{s+1}+a_{s+2}+……+a_t=(c-b)*m$，从而 $a_{s+1}+a_{s+2}+……+a_t$ 能够被$m$整除,证毕。
> **举栗子**：设$m=7$，且
> 整数为: $a[]=\{2,4,6,3,5,5,6\}$
> 前缀和: $s[]=\{2,6,12,15,20,25,31\}$
> 这些整数被$7$除时余数分别为
> $r[]=\{2,6,5,1,6,4,3\}$。有两个等于$6$的余数(位置是$2$和$5$)，这意味着结论：
> 从$2+1=3$开始，到$5$结束，有$a[3]+a[4]+a[5]=6+3+5=14$ 可被$7$整除。
### 四、鸽巢原理的应用
#### 1、练习题
一位洛谷$oier$要用$12$周的时间准备 $CTSC$,为了练习，他每天至少要刷一题，因为题目有难度，他每星期刷题无法超过$13$题。请你证明：存在连续的若干天期间，这位$oier$恰好刷了$11$题。
**证明**：
1.我们可以令$a_1$ 表示第一天所刷的题数，$a_2$ 表示前两天所刷的题数，$a_3$表示前三天所刷的题数.之后以此类推
2.而题目说，由于每天都要 **至少** 刷$1$题，所以数列
$$a_1<a_2<a_3<...<a_{84}$$
另有$a_1 >=1$.又每周最多刷$13$题，故$a_{84}< = 13 ∗ 12 = 156$。
因此又有：
$1 < = a_1 < a_2 < a_3 < . . . < a_{84} < = 156$
同理，
$a_1+11,a_2+11,a_3+11,...,a_{84} +11$同样是一个严格递增序列。范围：
$1+11 < = a_1+11 < a_2+11 < a_3+11 < . . . < a_{84}+11 < = 156+11$
$12<=a_1+11 < a_2+11 < a_3+11 < . . . < a_{84}+11<=167$
我们把两个序列合起来看：
$a_1 ,a_2,a_3,...,a_{84},a_1+11,a_2+11,a_3+11,...,a_{84} +11$
一共$168$个数。其中每一个数都是$1$到$167$之间的一个整数。
根据鸽巢原理可得，其中必有两个数相等！！！
同时$a_1,a_2,a_3,...,,a_{84}$中必然无相等的两个数，
而$a_1+11,a_2+11,a_3+11,...,a_{84} +11$中也是一样没有相等的两个数，那么，必然存在一个$x$和$y$,使得
$$\large a_x=a_y+11$$
从而得出结论：这个$oier$在第$y+1,y+2,y+3,...,x$天内一共刷了$11$道题。
#### 2、练习题
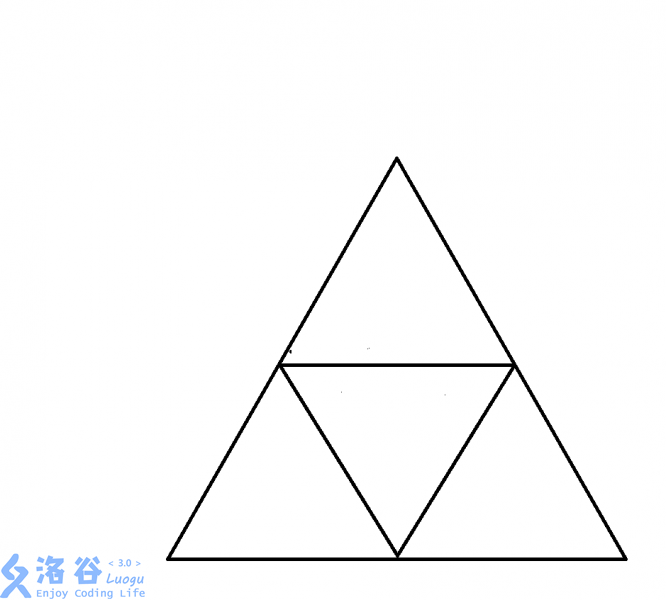
证明：在边长为$2$的等边三角形 **内部** 放上$5$个点。则至少存在两个点，他们之间的距离小于等于$1$.
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202311241310117.png)
我们先画出一个边长为$2$的等边三角形。
然后把三条边中点两两相连。就形成了这张图。
那么根据鸽巢原理，必然有两个点在一个边长为$1$的小三角形里。
而我们知道，边长为$1$的等边三角形里处处距离都小于等于$1$,于是问题就解决了
> $5$个鸽子，$4$个笼子。
#### 3、练习题
已知$n+1$个正整数，它们全都小于或等于$2n$，**证明当中一定有两个数是互质的**。
要证明这个问题，我们就要利用一个互质的特性：**两个相邻整数互质**。
有了这个突破口，于是我们可以构造$n$个鸽巢，每一个里依次放入
$1,2,3,4,...,2n$
这$2n$个数中的两个数。
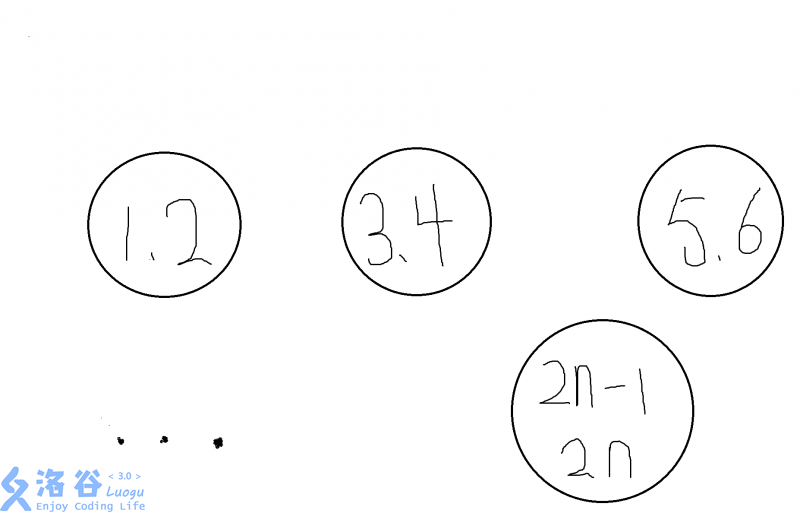
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202311241316080.png)
也就是说，我们要在这其中取出$n + 1$个数。
根据鸽巢原理，无论如何，我们都会抽空一个鸽巢。
一个鸽巢中的两个数肯定互质，所以问题就解决了。
> **扒栗史**：匈牙利大数学家厄杜斯($PaulErdous$,$1913 - 1996$) 向当年年仅$11$岁的波萨($LouisPósa$)提出这个问题，而小波萨思考了不足半分钟便能给出正确的答案。
> **冷笑话**：
> 山东高考$2017$年有$54$万人。而人的头发大约有$8−12$万根。那么必然有两人的头发数量相同。
#### 4、练习题
$NOIP$ 提高组 初赛 问题求解 习题集 $2010$ 第$3$题
记$T$为一队列，初始时为空，现有$n$个 **总和** 不超过$32$的正整数依次入列。如果无论这些数具体为何值，**都能找到一种出队的方式** ，使得存在某个时刻队列$T$中的数之和恰好为$9$，那么$n$的最小值是___________。
答案：
$18$
**题解**：
题意有些难懂：是指在数字尽可能取小，$n$尽可能长的情况下，符合题意的最大$n$值。
位置 `1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17`
数值 `1 1 1 1 1 1 1 1 (10) 1 1 1 1 1 1 1 1`
前缀和`1 2 3 4 5 6 7 8 18 19 20 21 22 23 24 25 26`
位置$9$取值是$10$的原因是，**起刁难作用**，让数组元素前缀和尽量的达不到$9$.
又因为，总的前缀和是$32$,故位置$9$的 **最小取值** 是$10$.
位置$10$开始，都用尽可能小的正数，故$1$最理想。
可以设置数据到数组的第$17$位元素，此时还是无法打成某段前缀和是$9$.
和是$32$,前$17$位已经用去了$26$，还剩下$6$,故第$18$位可以获得的数据是$1,2,3,4,5,6$
若第$18$位数值是$1$,
位置`10 11 12 13 14 15 16 17 18`
数值`1 1 1 1 1 1 1 1 1`
位置$10$到位置$18$可以构成和值为`1+1+1+1+1+1+1+1+1=9`.
若第$18$位数值是$2$,
位置`11 12 13 14 15 16 17 18`
数值`1 1 1 1 1 1 1 2`
位置$11$到位置$18$可以构成和值为`1+1+1+1+1+1+1+2=9`.
若第$18$位数值是$3$,
位置`12 13 14 15 16 17 18`
数值`1 1 1 1 1 1 3`
位置$11$到位置$18$可以构成和值为`1+1+1+1+1+1+3=9`.
若第$18$位数值是$4$,
位置`13 14 15 16 17 18`
数值`1 1 1 1 1 4`
位置$11$到位置$18$可以构成和值为`1+1+1+1+1+4=9`.
若第$18$位数值是$5$,
位置`14 15 16 17 18`
数值`1 1 1 1 5`
位置$11$到位置$18$可以构成和值为`1+1+1+1+5=9`.
若第$18$位数值是$6$,
位置`15 16 17 18`
数值`1 1 1 6`
位置$11$到位置$18$可以构成和值为`1+1+1+6=9`.
很明显，在极端条件下，符合题意的$n$值，是$18$.
#### 5、练习题
从整数$1,2,...,200$中选出$101$个整数。
**求证**：在所选的这些整数之间存在两个这样的整数，其中的一个可被另一个整除。
首先要先知道这点：任一整数都可以写成的$2^k*a$形式，其中$k>=0\&\&a$是奇数。
对于$1$到$200$之间的一个整数，$a$是$100$个数$1,3,5，...，199$中的一个。因此，在所选的$101$个整数中存在两个整数，当写成上述形式时这两个数具有相同的$a$值。令这两个数是$2^r*a$和$2^s*a$，如果$r<s$,那么第二个数就能被第一个数整除。反之亦然。
注意，从$1,2，...，200$中可以选择$100$个数，使得其中没有一个能被另一个数整除（比如，这$100$个整数是$101,102，...，119,200$）
### 五、$Ramsey$定理
> **扒栗史**：此定理由$Frank$ $Plumpton$ $Ramsey$（弗兰克·普伦普顿·拉姆齐，$1903−1930$）提出.
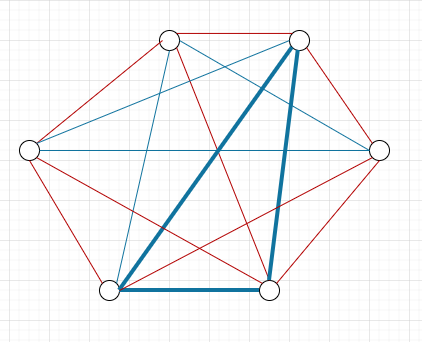
此定理有一个广为流传的例子：$6$ 个人中至少存在$3$人相互认识或者相互不认识。
**转换**：该定理等价于证明这$6$个顶点的完全图的边，用红、蓝二色任意着色，必然至少存在一个红色边三角形，或蓝色边三角形
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202311241334465.png)
### 六、与编程结合的题目
**[$HDU$ $1808$ $Halloween$ $treats$](https://acm.hdu.edu.cn/showproblem.php?pid=1808)**
**题目大意**：
给你两个整数$C$和$N$，再给你$N$个正数的序列，从中找到若干数，使得其和刚好是 $C$ 的倍数。输出这些数的序号。
我们知道$C<=N$的，故我们可以用鸽巢原理去做，
**思路**：
$Sum[i]$为序列中前 $i$ 项的和。则有两种可能：
1.若有 $Sum[i]$ 是 $C$ 的倍数，则直接输出前 $i$ 项。
2.如果没有任何的 $Sum[i]$ 是 $C$ 的倍数，则计算 $ri = Sum[i] \% C$。根据鸽巢原理，肯定有 $Sum[i] \% C == Sum[j] \% C，j<i$。则第 $j +1$项到第 $i$ 项数的和即为 $C$ 的倍数。
这题说，要是没答案就输出 `no sweets` ，想想，这有可能吗？
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100;
int sum[N], mod[N];
int main() {
ios::sync_with_stdio(false);
int c, n;
while (cin >> c >> n, c + n) {
memset(mod, -1, sizeof mod);
memset(sum, 0, sizeof sum);
mod[0] = 0;
int s = 0, t = 0;
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
sum[i] = (sum[i - 1] + x) % c; // 前缀和 %c
if (sum[i] == 0) {
t = i;
continue;
}
if (mod[sum[i]] == -1)
mod[sum[i]] = i; // 首次出现这个余数
else { // 多次出现此余数
s = mod[sum[i]]; // 开始位置
t = i; // 结束位置
}
}
for (int i = s + 1; i <= t; i++)
cout << i << (i != t ? " " : "\n");
}
}
```
**[$HDU$ $1205$ 吃糖果](http://acm.hdu.edu.cn/showproblem.php?pid=1205)**
**方法**：隔板法求解
找出数量最多的一种糖果，把数量$n$看成$n$个隔板，隔成$n$个空间（隔板以右为一空间），其他糖果数量总和记为数值$s$。
（1）若$s<n-1$，把$s$个糖果放到隔板之间，$n$个隔板不够放，至少一个空间内没有糖果，因为两个隔板为同一种糖果，不符合题意，无解。
（2）若$s>=n-1​$，有解。
推导之后发现：当总数-最大值>=最大值-1时，就满足有解条件。
**注意事项**：
（1）用数组存放时，数组要开大，$n<=1000000$，数组要$a[1000000]$；
（2）把$t,n$等变量定义成`long long`类型（$int$类型的话为$WA$）。
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1000010;
int a[N];
signed main() {
int T;
cin >> T;
while (T--) {
int n, sum, mx;
cin >> n;
sum = 0, mx = 0;
for (int j = 0; j < n; j++) {
cin >> a[j];
sum += a[j];
mx = mx < a[j] ? a[j] : mx;
}
if ((sum - mx) >= (mx - 1))
puts("Yes");
else
puts("No");
}
}
```
**[$HDU$ $5917$ $Instability$](http://acm.hdu.edu.cn/showproblem.php?pid=5917)**
> 前导知识：
> **[离散数学 --- 图论基础 --- 子图和补图，握手定理](https://blog.csdn.net/qq_51947882/article/details/126751352)**
>
**题意**：给出一个图，求稳定子图的个数。稳定子图定义为包含三元环子图或者三个点独立集子图的图。
**题解**：
$Ramsey$定理的通俗表述： $6$ 个人中至少存在$3$人相互认识或者相互不认识。所以对于大于$6$的子集都是满足条件的，组合数算一下就好，对于小于$6$的子集，最多是$n$的5次方，直接暴力。
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
const int M = 1e2 + 7;
const int P = 1e9 + 7;
int T, n, m, cas = 1;
int g[M][M];
int fac[M];
// 快速幂
int qmi(int a, int b) {
int res = 1;
a %= P;
while (b) {
if (b & 1) res = res * a % P;
b >>= 1;
a = a * a % P;
}
return res;
}
/*
Q:什么是费马小定理?
答：费马小定理是一个关于模运算的定理，它陈述了如果p是一个质数，而a是任意整数且不是p的倍数，
那么a^(p-1) 与 1 (mod p) 同余。
Q:费马小定理是怎么求逆元的？
答：当p是质数时，我们分离一项出来
a * a^(p−2) ≡ 1 (mod p)
对比逆元的方程式，可以很容易得到，a关于p的逆元就是 a^(p −2),而a^(p-2)可以用快速幂求得
Q:组合数公式C(n,m)=n!/(m!*(n-m)!) ，由于需要取模，同时存在除法，所以可以考虑是否可以用费马小定理求除法逆元？
答：是可以的，原因：因为模mod=1e9+7是质数，并且，题目中的数据范围n<=50,是不可能是mod的倍数的，所以符合费马小定理
的要求，可以用费马小定理来求除法逆元。
*/
int C(int n, int m) {
/*
fac[n]: n!
qmi(fac[m], P - 2) : 费马小定理的结果 (m!)^(p-2),这样，把除m!取模 转化为乘 (m!)^(p-2)后取模
qmi(fac[n - m], P - 2) :同上
*/
return fac[n] * qmi(fac[m], P - 2) % P * qmi(fac[n - m], P - 2) % P;
}
int judge3(int i, int j, int k) { // 判断三点之间满不满足不稳定点集
if (g[i][j] && g[i][k] && g[j][k]) return 1; // 三点之间相连
if (!g[i][j] && !g[i][k] && !g[j][k]) return 1; // 三点之间不互连
return 0;
}
int judge4(int i, int j, int k, int l) {
if (judge3(i, j, k) || judge3(i, j, l) || judge3(j, k, l) || judge3(i, k, l)) return 1;
// 表示4个点中有三个点为不稳定点集就行,为什么呢？
// 因为时题目要求的，不稳定点集为3个点。
return 0;
}
int judge5(int i, int j, int k, int l, int o) {
// 表示5个点中有4个点满足就行
if (judge4(i, j, k, l) || judge4(i, j, k, o) || judge4(i, j, l, o) || judge4(j, k, l, o)
|| judge4(i, k, l, o)) return 1;
return 0;
}
void solve() {
cin >> n >> m; // n个顶点,m条边
memset(g, 0, sizeof g); // 初始化地图
while (m--) {
int a, b;
cin >> a >> b;
g[a][b] = g[b][a] = 1; // 无向图
}
int ans = 0;
if (n >= 6) {
ans = qmi(2, n);
// ① 多项式定理C(n,0)+C(n,1)+...+C(n,n)=2^n
// ② 也可以这样来思考，一个也不要，要1个，要2个，要3个，...,要n个
// C(n,k)(k>=6)表示，从n个中取k个出来，总存在一个不稳定点集的个数（三点之间互联或三点之间不连）
for (int i = 0; i < 6; i++) /// 减去前5个
ans = (ans - C(n, i) + P) % P;
}
if (n >= 3) { // 枚举任意3个
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++)
for (int k = j + 1; k <= n; k++)
if (judge3(i, j, k)) ans = (ans + 1) % P;
}
if (n >= 4) { // 暴力取4个
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++)
for (int k = j + 1; k <= n; k++)
for (int l = k + 1; l <= n; l++)
if (judge4(i, j, k, l)) ans = (ans + 1) % P;
}
if (n >= 5) { // 暴力取5个
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++)
for (int k = j + 1; k <= n; k++)
for (int l = k + 1; l <= n; l++)
for (int o = l + 1; o <= n; o++)
if (judge5(i, j, k, l, o)) ans = (ans + 1) % P;
}
printf("Case #%lld: %lld\n", cas++, ans);
}
signed main() {
// 加快读入
ios::sync_with_stdio(false), cin.tie(0);
// 预处理阶乘数组（同步取模）
fac[0] = 1, fac[1] = 1;
for (int i = 2; i < M; i++) fac[i] = fac[i - 1] * i % P;
cin >> T;
while (T--) solve();
}
```
https://blog.csdn.net/LJD201724114126/article/details/84547302