|
|
|
|
|
|
|
|
|
|
|
## 巧用隔板法快速攻破排列组合难题
|
|
|
|
|
|
|
|
|
|
|
|
**问题**:如果让你把$7$个大小相同的橘子分给$4$个小朋友,要求每个小朋友至少分到$1$个橘子,问一共有多少种不同的分法?
|
|
|
|
|
|
|
|
|
|
|
|
看完问题后,你能快速得出答案吗?如果难倒你的话,那就说明你对排列组合中的隔板法还不太了解哦!
|
|
|
|
|
|
|
|
|
|
|
|
<center><img src='https://pic3.zhimg.com/80/v2-245ea34fddd3c999f668eef8b68e4e0e_1440w.webp'></center>
|
|
|
|
|
|
|
|
|
|
|
|
**首先,让我们一起来正确认识一下隔板法**
|
|
|
|
|
|
|
|
|
|
|
|
隔板法主要针对的是 **相同元素** 的不同分堆问题。我们也可以把它理解为:
|
|
|
|
|
|
|
|
|
|
|
|
如果把$n$个相同的元素分给$m$个不同的对象,每个对象 **至少有一个** ,**问有多少种不同的分法的问题**。其基本公式为:
|
|
|
|
|
|
$$\large C_{n-1}^{m-1}$$
|
|
|
|
|
|
|
|
|
|
|
|
**然后,再来看一下隔板法都有哪些题型特征**
|
|
|
|
|
|
|
|
|
|
|
|
隔板法一共有三种题型:**①标准型、②多分型、③少分型**,后两种都需要基于 **标准型** 来解题,具体要怎么操作呢?下面我们再来通过$3$个例题分别介绍一下隔板法的三种题型特征及应用,接着往下看
|
|
|
|
|
|
<center><img src='https://pic2.zhimg.com/v2-8d1871f1b8b4c562d301b4572a79b7e5_b.webp'></center>
|
|
|
|
|
|
|
|
|
|
|
|
#### 1、标准型
|
|
|
|
|
|
标准型需要同时具备的$3$个要求:
|
|
|
|
|
|
* 被分配的$n$个元素无差别
|
|
|
|
|
|
* 这$n$个元素分给$m$个不同对象
|
|
|
|
|
|
* 每个对象至少分 **一个** 元素
|
|
|
|
|
|
|
|
|
|
|
|
<center><img src='https://pic2.zhimg.com/80/v2-331e2de48f14d04389c7947ca5e3619d_1440w.webp'></center>
|
|
|
|
|
|
|
|
|
|
|
|
**【解析】正确答案为$C$。**
|
|
|
|
|
|
|
|
|
|
|
|
【解题思路】本题中相同的元素是$6$本相同的书,故$n=6$;放进$4$个抽屉,即将书分成$4$堆,故$m=4$;每个抽屉至少放$1$本书,故本题为隔板法中的标准题型。
|
|
|
|
|
|
|
|
|
|
|
|
【解题方法】把$6$本书排成一排,因为书是相同的,不存在排列顺序问题。要把这$6$本书分成$4$堆,只要在这$6$本书形成的空隙中插入$3$个隔板即可。$6$本书排成一排,形成了$7$个空。但是,因为要求每个抽屉至少放$1$本书,所以最前面的空和最后一个空是不能插板的,则只能在中间形成的$5$个空中插入$3$个隔板,即从$5$个空中选择$3$个空插入隔板,代入公式:
|
|
|
|
|
|
<center><img src='https://pic1.zhimg.com/80/v2-5ba7bf9f7add0fd56372474c63596060_1440w.webp'></center>
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 2、多分型
|
|
|
|
|
|
多分型需要同时具备的$3$个要求:
|
|
|
|
|
|
* 被分配的$n$个元素无差别
|
|
|
|
|
|
* 这$n$个元素分给$m$个不同的对象
|
|
|
|
|
|
* 每个对象至少分$x$个元素
|
|
|
|
|
|
|
|
|
|
|
|
<center><img src='https://pic4.zhimg.com/80/v2-7a5a09f2f317c97d06d7d34b17fdd57b_1440w.webp'></center>
|
|
|
|
|
|
|
|
|
|
|
|
**【解析】正确答案为$D$。**
|
|
|
|
|
|
|
|
|
|
|
|
【解题思路】此题中没有要求至少发$1$份,而是要求至少发$9$份的,因此需要将其 **转化** 为标准型的隔板模型,方法就是 **先每个部门分$x-1$个元素,剩下的元素就转化为每个部门至少分一个元素了**。
|
|
|
|
|
|
|
|
|
|
|
|
【解题方法】假设三个部门分别为$A、B、C$,每个部门可以先分$8$份,然后再把剩下的$6$份发给$3$个部门,保证每个部门发$1$份,**代入公式**:
|
|
|
|
|
|
|
|
|
|
|
|
<center><img src='https://pic2.zhimg.com/80/v2-c98fb6ab48df65214626b43914de67c9_1440w.webp'></center>
|
|
|
|
|
|
|
|
|
|
|
|
#### $3$、少分型
|
|
|
|
|
|
少分型需要同时具备的$3$个要求:
|
|
|
|
|
|
* 被分配的$n$个元素无差别
|
|
|
|
|
|
* 这$n$个元素被分给$m$个不同的对象
|
|
|
|
|
|
* 被任意分给这$m$个不同的对象
|
|
|
|
|
|
|
|
|
|
|
|
<center><img src='https://pic2.zhimg.com/80/v2-08be951c208da9a8c560d86c353aa8d1_1440w.webp'></center>
|
|
|
|
|
|
|
|
|
|
|
|
【**解析**】正确答案为$B$。
|
|
|
|
|
|
|
|
|
|
|
|
【**解题思路**】这道题中说每个盒子可以为空,就意味着有的盒子可以分$0$个元素,因此可以采用 **先借后还** 的思路,先向每一个盒子借一个元素,总共就会有$n$个元素了,由于借了一个元素,接下来在分的时候,每个盒子则 **至少需要分一个**,这样就 **转化** 成了 **标准的隔板模型**。
|
|
|
|
|
|
|
|
|
|
|
|
【**解题方法**】在分之前先向每个盒子借$3$个小球,总共就会有$23$个小球,接下来分的时候需要再给每个盒子一个小球,就变成每个盒子至少分一个小球了,有多少种分法,代入公式:
|
|
|
|
|
|
<center><img src='https://pic2.zhimg.com/80/v2-847624b34f207f6ec7e6d3f556a75511_1440w.webp'></center>
|
|
|
|
|
|
|
|
|
|
|
|
以上就是今天所讲的排列组合之隔板法的运用了,希望大家理解并能熟练运用!
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【**上文解锁**】一共有$20$种不同的分法,你做对了吗?
|
|
|
|
|
|
【**解析**】此题为隔板法的标准型,因为相同的元素是$7$个大小相同的橘子,故$n=7$;给$4$个小朋友,故$m=4$;所以只要在这$7$个橘子$6$个空之间插入$3$个隔板即可,代入公式:
|
|
|
|
|
|
|
|
|
|
|
|
<center><img src='https://pic3.zhimg.com/80/v2-c78295406b71842e6df90f4b1458e082_1440w.webp'></center>
|
|
|
|
|
|
|
|
|
|
|
|
### 回到本题
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
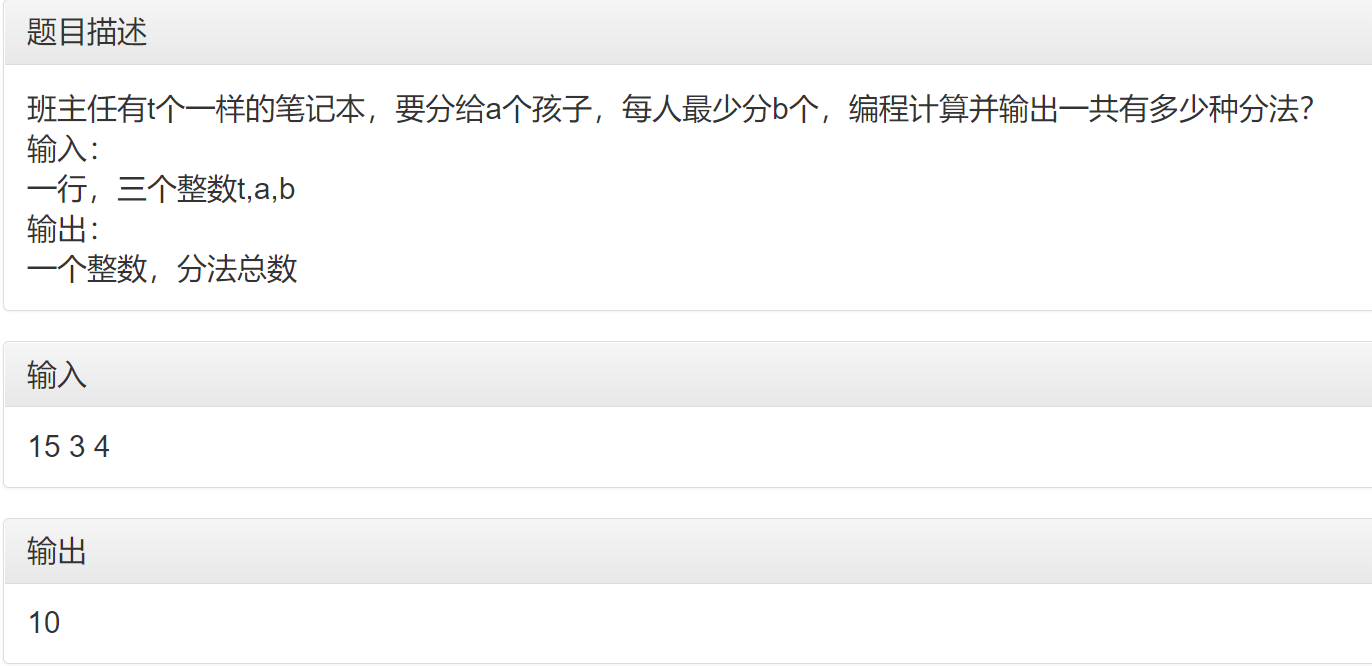
$15$个笔记本,分给$3$个小朋友,每人最少分$4$个,属于【多分型】,先每人分$3$个,预处理一下:
|
|
|
|
|
|
$$\large 15-3*3=6$$
|
|
|
|
|
|
|
|
|
|
|
|
$$\LARGE ○ ○ ○ ○ ○ ○$$
|
|
|
|
|
|
|
|
|
|
|
|
属于在$5$个有用的 **空格** 中选择$2$个,即
|
|
|
|
|
|
|
|
|
|
|
|
$$\large C_5^2=\frac{5\times 4}{ 2 \times 1}=10$$
|