python/TangDou/Topic/扩展欧拉定理.md

## [指数循环节&欧拉降幂](https://blog.csdn.net/acdreamers/article/details/8236942)

### 一、问题
比如计算 $$\large A^B \ \% \ C$$

其中$1 \leq B \leq 10^{20000000}$ 和 $1 \leq C \leq 10^6$

$b$过大，使用暴力和快速幂是无法求解的。

### 二、扩展欧拉定理公式
- ① 当$B \geq \phi(C)$时：
$$\large A^B \% C = A^{B \% \phi(C)+\phi(C)} \% C $$
> 这是广义降幂公式，不要求$A$与$C$互质！

- ② 当$B<φ(C)$时，就没有降幂的必要了
  

### 三、练习题

**[$P5091$ 【模板】扩展欧拉定理](https://www.luogu.com.cn/problem/P5091)**

**题意**：
给定$A$,$B$和$C$的值，求$A^B \ mod \ C$的值。其中$1 \leq A,C \leq 10^9,1 \leq B \leq 10 ^{1000000}$。

**特点**
欧拉降幂，模板题

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
const int N = 2000010;

// 求单个数字的欧拉函数
int phi(int x) {
    int res = x;
    for (int i = 2; i <= x / i; i++)
        if (x % i == 0) {
            res = res / i * (i - 1);
            while (x % i == 0) x /= i;
        }
    if (x > 1) res = res / x * (x - 1);
    return res;
}

// 快速幂
int qmi(int a, int b, int p) {
    int res = 1;
    a %= p;
    while (b) {
        if (b & 1) res = res * a % p;
        b >>= 1;
        a = a * a % p;
    }
    return res;
}

signed main() {
    int a, c;
    cin >> a >> c;
    int p = phi(c);

    // 将非数字字符，比如空格读没
    char ch;
    ch = getchar();
    while (ch < '0' || ch > '9') ch = getchar();

    // 当是数字字符时，一直读入
    int b = 0;
    while (ch >= '0' && ch <= '9') {
        b = b * 10 + ch - '0';
        if (b >= p) // 检查b是否大于等于phi(c)
            b = b % p + p;
        // 继续读入下一个字符
        ch = getchar();
    }
    printf("%lld\n", qmi(a, b, c)); // 按快速幂来计算就行了
}
```

**[$HDU2837$ $Calculation$](https://acm.hdu.edu.cn/showproblem.php?pid=2837)**

**题意**：$f(0) = 1$ $and$ $0^0=1$. $f(n) = (n\%10)^{f(n/10)}$ 求$f(n)\%m$。

就递归加指数循环节，
$$\large f(n)\%m = (n\%10)^{f(n/10)\% \phi(m)+ \phi(m)}\%m$$

然后继续计算一下指数部分：

$f \large (n/10)\%\phi(m)=(n/10\%10)^{f(n/10/10)\%\phi(\phi(m))+\phi(\phi(m))}\%\phi(m)$

一层层递归，直到$n==0$的话，此时$0^0=1$，就返回$1\%$当前要$mod$的那个数了，

我们设当前$dfs$到的层中表达式为$f(x)$，当前的$\phi$为$\phi(y)$,
我们需要判断$f(x)$是不是大于$phi(y)$,如果大于则用扩展欧拉定理进行进步化化简，否则直接计算。

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"

// 求单个数字的欧拉函数
int phi(int x) {
    int res = x;
    for (int i = 2; i <= x / i; i++)
        if (x % i == 0) {
            res = res / i * (i - 1);
            while (x % i == 0) x /= i;
        }
    if (x > 1) res = res / x * (x - 1);
    return res;
}

// 快速幂
int qmi(int a, int b, int p) {
    int res = 1;
    a %= p;
    while (b) {
        if (b & 1) res = res * a % p;
        b >>= 1;
        a = a * a % p;
    }
    return res;
}

// a^b 与 c 谁大谁小？
// 返回 a^x<=c的第一个a^x,其中x ∈ [1,b]
// 如果跑完b，还是 a^b <=c, 就返回 a^b
int check(int a, int b, int c) {
    int res = 1;
    while (b--) {
        res *= a;
        if (res >= c) return res;
    }
    return res;
}

int dfs(int a, int c) {
    if (a == 0) return 1;
    int p = phi(c);

    // f(n/10)
    int x = dfs(a / 10, p);
    int y = check(a % 10, x, c);
    if (y >= c) {
        int res = qmi(a % 10, x + p, c);
        if (res == 0) res += c;
        return res;
    } else
        return y;
}

signed main() {
    int T;
    cin >> T;
    while (T--) {
        int a, c;
        cin >> a >> c;
        cout << dfs(a, c) % c << endl;
    }
}
```
> <font color='red' size=4><b>注：这个代码没看懂，$TODO$，待续</b></font> 


[$HDU4335$ $What$ $is$ $N?$](https://acm.hdu.edu.cn/showproblem.php?pid=4335)

题意：给定$3$个整数$b,p,M$，其中$0 \leq b <p,1 \leq p \leq 10^5 $和$1 \leq M \leq 2^{64}-1$，求满足下面两个条件的$n$ 的个数。

![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202311151419918.jpeg)

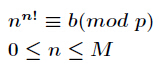
**分析**：
由$$\large n ^{n! \% \phi(p)+\phi(p)} \% p \equiv b$$

所以这样就容易多了，注意有个特判。


BZOJ3884: 上帝与集合的正确用法
https://www.cnblogs.com/jiecaoer/p/11442358.html

TODO 挖坑等填
https://www.cnblogs.com/LMCC1108/p/11252888.html