python/TangDou/Mkx/错排公式.md

## 错排公式
http://t.zoukankan.com/lemonbiscuit-p-7776135.html

错排问题最早被　**尼古拉·伯努利和欧拉**　研究，因此历史上也称为伯努利-欧拉的装错信封的问题。这个问题有许多具体的版本，如在写信时将$n$封信装到$n$个不同的信封里，有多少种全部装错信封的情况？又比如四人各写一张贺年卡互相赠送，有多少种赠送方法？自己写的贺年卡不能送给自己，所以也是典型的错排问题。

**举例**：

① 十本不同的书放在书架，现重新摆放，使得每本书都不在原来的位置上，有几种摆法？
② 一个人给十个同学写信，但他把所有的信都装错了信封，问共有多少种错误的方式？

[神、上帝以及老天爷](http://acm.hdu.edu.cn/showproblem.php?pid=2048)
<center><img src='https://upload-images.jianshu.io/upload_images/17434829-e3aceb62ac90ee17.png?imageMogr2/auto-orient/strip|imageView2/2/w/883/format/webp'></center>

###　解题思路
做这道题刚开始没有什么头绪，后来上网查了一下才发现原来有一个错排公式，也就是元素都不在对应原来位置的方法数。公式为：
$$\large f(n) = (n-1) \times (f(n-2) + f(n-1))$$

**推导过程**：

对递归公式进行解释：

$n$个不同的元素的一个错排公式可以分作两步完成：

第一步：假设我们错排第一个元素，那么它可以从$2\sim n$的位置任意选择其中的一个，一共是有$n-1$种选择。

第二步：错排其余$n-1$个元素，也是需要分情况和种类的。因为这需要看第一步的结果，如果第一个元素落在第$k$个位置上，第二步就需要把$k$号元素进行错排，$k$号元素错排位置的不同将导致不同的情况会发生：
* 假设$k$号元素正好落在了第一个元素的位置，那么就可以将第一个元素和第$k$个元素完全剔除出去，因为相当于只是他们两者互换了位置，其他元素暂时还没有发生变动。留下来的$n-2$元素进行错排的话，那么我们就可以得到了$f(n-2)$种的错排方式。
  

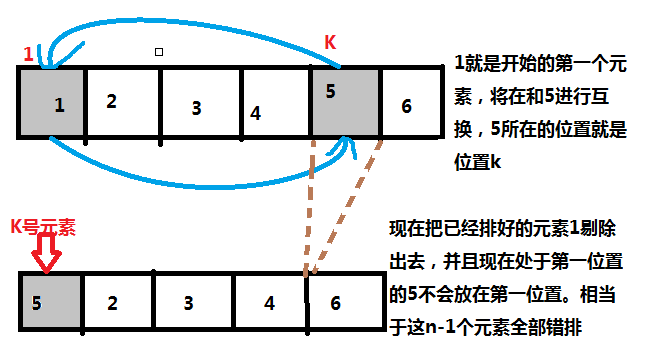
* 若$k$号元素不排到第一个元素的位置，我们可以暂时将现在排在$k$号位置的第一个元素剔除出去，剩下来的就只包含$k$号元素和原来$n-2$个的元素了。这时，我们可以将原来的第一个元素的位置看做是现在$k$号元素的原本位置，因为$k$号元素不能够放在原来的位置上，所以就相当于是原来的$n-2$个元素和$k$共计$n-1$个元素进行完全的错排,那么一共就有$f(n-1)$种方法。

第二种情况希望大家仔细理解！配一张图便于理解

![](http://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/2022/12/1375c9ead1d7dd634893247aee7445ec.png)

那么，我们有根据加法原理，完成第二步有$f(n-2)+f(n-1)$种方法。

根据乘法原理得到:
$$\large f(n)=(n-1)\times (f(n-1)+f(n-2))$$
递推关系解释完毕。


有了**错排公式**，这道题就很容易解决了，总的排列方法数有$n$的**阶乘**个，而全部错排的方法数有 $(n-1)\times (f(n-1) + f(n-2))$个，最后直接把**错排方法数除以总的排列数**，然后注意输出格式就可以了。

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
typedef long long LL;
LL f[N], sum;
// f(n)=(n-1)*(f(n-1)+f(n-2))
int main() {
    int m;
    scanf("%d", &m);

    while (m--) {
        int n;
        scanf("%d", &n);
        // base case
        sum = 1;
        f[1] = 0, f[2] = 1;

        //递推出错排次数
        for (int i = 3; i <= n; i++)
            f[i] = (i - 1) * (f[i - 1] + f[i - 2]);

        //总次数
        for (int i = 1; i <= n; i++) sum = sum * i;

        //比率
        printf("%.2lf%%\n", (double)f[n] / sum * 100);
    }
    return 0;
}
```


[不容易系列之(4)——考新郎](http://acm.hdu.edu.cn/showproblem.php?pid=2049)
<center><img src='https://upload-images.jianshu.io/upload_images/17434829-611e0b0ac9a6bb8c.png?imageMogr2/auto-orient/strip|imageView2/2/w/784/format/webp'></center>

<center><img src='https://www.freesion.com/images/724/f8c6d34224f1e2f2d8d13dfa9f729634.JPEG'></center>

将总数为$n$个人的一队人，将选错新娘的放在一起则构成一个 **全错排列**，将选对的$n-m$个新郎放在一起成为一个排列，则可能出现的总数为正确的排列情况*全错排的情况

复习一下组合数公式：

$$\large C_a^b=\frac{a!}{b!\times (a-b)!}$$

```cpp {.line-numbers}
#include <iostream>
using namespace std;
typedef long long LL;

LL C(int a, int b) {
    LL sum1 = 1, sum2 = 1;
    for (int i = b + 1; i <= a; i++) sum1 *= i;
    for (int i = 1; i <= a - b; i++) sum2 *= i;
    return sum1 / sum2;
}
int main() {
    LL f[21] = {0, 0, 1}; //这个初始化很牛B的样子,放过头雁打二雁，而且f[1]=0,f[2]=1
    //错排公式,预处理
    for (int i = 3; i < 21; i++) f[i] = (i - 1) * (f[i - 1] + f[i - 2]);

    int T;
    cin >> T;
    while (T--) {
        int n, m;
        cin >> n >> m;
        cout << C(n, m) * f[m] << endl;
    }
    return 0;
}
```