|
|
|
|
|
# $stack$
|
|
|
|
|
|
|
|
|
|
|
|
### 题目描述
|
|
|
|
|
|
小 $\mathcal{L}$ 有一个栈和一个队列,现在队列中有 $n$ 个**不同**元素,每次可以选择两种操作:
|
|
|
|
|
|
|
|
|
|
|
|
1. 把队头的元素放到栈顶(如果队列为空则不能进行该操作)
|
|
|
|
|
|
2. 把栈顶元素放入输出数组(如果栈为空则不能进行该操作)
|
|
|
|
|
|
|
|
|
|
|
|
现在总共要进行 $2n$ 次操作,故输出数组长度必然为 $n$。
|
|
|
|
|
|
|
|
|
|
|
|
小 $\mathcal{L}$ 有强迫症,所以输出数组的第一个位置的元素有必须是自己喜欢的。
|
|
|
|
|
|
|
|
|
|
|
|
现在给出队列($a_1\sim a_n$ 其中 $a_1$ 为队头)中的元素的属性($a_i$ 为 $1$ 则表示该元素小 $\mathcal{L}$ 喜欢,为 $0$ 则不喜欢),您需要求出符合小 $\mathcal{L}$ 要求的不同的出栈入栈方式的个数,因为结果很大,所以您只需要给出结果 $\bmod 998244353$ 后的结果即可。
|
|
|
|
|
|
|
|
|
|
|
|
### 输入格式
|
|
|
|
|
|
|
|
|
|
|
|
输入包含两行。
|
|
|
|
|
|
|
|
|
|
|
|
第一行输入一个正整数 $n$。
|
|
|
|
|
|
|
|
|
|
|
|
第二行输入 $n$ 个正整数 $a_1,a_2,...,a_n$。
|
|
|
|
|
|
|
|
|
|
|
|
### 输出格式
|
|
|
|
|
|
|
|
|
|
|
|
输出一个正整数表示答案。
|
|
|
|
|
|
|
|
|
|
|
|
### 数据范围
|
|
|
|
|
|
|
|
|
|
|
|
对于 $20\%$ 的数据 $n\leq 10$。
|
|
|
|
|
|
|
|
|
|
|
|
对于 $40\%$ 的数组 $n\leq 2333$。
|
|
|
|
|
|
|
|
|
|
|
|
对于另外 $20\%$ 的数据仅存在 $a_1$ 的值为 $1$。
|
|
|
|
|
|
|
|
|
|
|
|
对于另外 $20\%$ 的数据仅存在唯一的 $i$,使得 $a_i=1$。
|
|
|
|
|
|
|
|
|
|
|
|
对于 $100\%$ 的数据 $n\leq1\times 10^6$,$a_i\in\{0,1\}$。
|
|
|
|
|
|
|
|
|
|
|
|
<div style="page-break-after: always"></div>
|
|
|
|
|
|
|
|
|
|
|
|
### 题解
|
|
|
|
|
|
首先对于任意一个最终的输出数组可以通过反推,得到一个唯一的操作序列,所以说合法的操作序列与输出数组是一一对应的,也就是说输出数组的种类数等价于合法的操作序列数。所以只需要考虑合法的方案数即可。
|
|
|
|
|
|
|
|
|
|
|
|
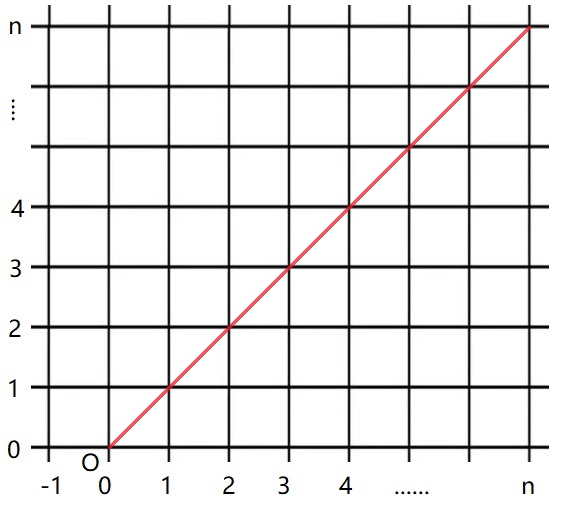
考虑一个合法的输出时如何产生的,因为开头必须为 $1$,所以可以先指定开头的元素,那么要将这个元素前面的元素都先放入栈中,这个元素才能作为第一个。假设这个元素为第 $i$ 个,那么 $1\sim i-1$ 在栈中,$i+1\sim n$ 在队列中。也就是说问题变成了一个栈中已经存在一定元素出出栈序列数。考虑一个经典的转化,出栈数计数这类问题可以放到方格图中,如下
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中经典的 $n$ 不同元素出栈序列问题是从 $(0,0)$ 出发到 $(n,n)$,但是不能到红线上方的区域的方案数。也就是将入栈等同于向右走,出栈等同于向上走,因为要保证在任意一个出栈操作前已经有入栈的个数必须大于出栈的个数所以存在红线的限制。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
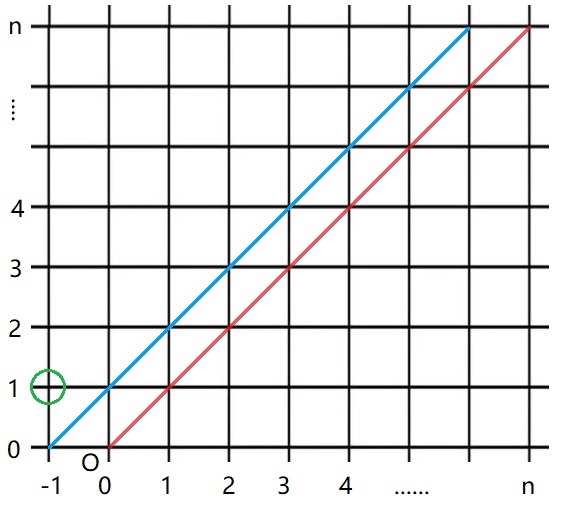
要解决这个问题。可以发现对于任意的越过红线的方案都会经过蓝线,所以考虑那些不合法的方案,也就是必定经过蓝线的方案。找到起点 $(0,0)$ 关于蓝线的对称点 $(-1,1)$,可以发现从 $(-1,1)$ 除法的每一条到 $(n,n)$ 的路径都会经过蓝线,再将所有这些路径以第一次经过蓝线上的点为界限将前面按蓝线对称,这样起点又边了 $(0,0)$,并且不难发现这些方案与那些不合法方案是一一对应的(不理解的话可以自己画几条路径,总能找到为一条从 $(-1,1)$ 出发的路径按上述方法与之对应)
|
|
|
|
|
|
|
|
|
|
|
|
于是可以得出 $f(n)={2n\choose n}-{2n\choose n-1}=\frac{2n\choose n}{n+1}$,也就是著名的 **卡特兰数**。
|
|
|
|
|
|
|
|
|
|
|
|
现在相当于起点位置变成了 $(i-1,0)$ 终点变成了 $(n-1,n-1)$,做法仍然类似,找到起点关于蓝线对称的点,计算其到终点的方案数便是不合法的方案数。对称后点的坐标为 $(-1,i)$,所以答案就是 ${2n-i-1\choose n-1}-{2n-i-1\choose n}$。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 参考代码
|
|
|
|
|
|
|
|
|
|
|
|
```c++{.line-numbers}
|
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
|
|
|
const int maxn = 1e6 + 10;
|
|
|
|
|
|
const int mod = 998244353;
|
|
|
|
|
|
int n, f[maxn];
|
|
|
|
|
|
int fac[maxn << 1];
|
|
|
|
|
|
int inv[maxn << 1];
|
|
|
|
|
|
int qmi(int a, int b, int mod) {
|
|
|
|
|
|
a %= mod;
|
|
|
|
|
|
if (!a) {
|
|
|
|
|
|
return 0;
|
|
|
|
|
|
}
|
|
|
|
|
|
int result = 1;
|
|
|
|
|
|
for (; b; a = 1ll * a * a % mod, b >>= 1) {
|
|
|
|
|
|
if (b& 1) {
|
|
|
|
|
|
result = 1ll * result * a % mod;
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
return result;
|
|
|
|
|
|
}
|
|
|
|
|
|
int C(const int n, const int m) {
|
|
|
|
|
|
if (n < m) {
|
|
|
|
|
|
return 0;
|
|
|
|
|
|
}
|
|
|
|
|
|
return 1ll * fac[n] * inv[m] % mod * inv[n - m] % mod;
|
|
|
|
|
|
}
|
|
|
|
|
|
int cal(int a, int b) {
|
|
|
|
|
|
return(1ll * C(a + 2 * b, b) - C(a + 2 * b, b - 1) + mod) % mod;
|
|
|
|
|
|
}
|
|
|
|
|
|
void init(const int n) {
|
|
|
|
|
|
fac[0] = 1;
|
|
|
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
|
|
|
fac[i] = 1ll * fac[i - 1] * i % mod;
|
|
|
|
|
|
}
|
|
|
|
|
|
inv[n] = qmi(fac[n], mod - 2, mod);
|
|
|
|
|
|
for (int i = n - 1; i >= 0; i--) {
|
|
|
|
|
|
inv[i] = inv[i + 1] * (i + 1ll) % mod;
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
|
|
|
freopen("stack.in", "r", stdin);
|
|
|
|
|
|
freopen("stack.out", "w", stdout);
|
|
|
|
|
|
scanf("%d", &n);
|
|
|
|
|
|
init(n << 1);
|
|
|
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
|
|
|
scanf("%d", &f[i]);
|
|
|
|
|
|
}
|
|
|
|
|
|
int ans = 0;
|
|
|
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
|
|
|
if (f[i]) {
|
|
|
|
|
|
ans = (ans + cal(i - 1, n - i)) % mod;
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
cout << ans << endl;
|
|
|
|
|
|
return 0;
|
|
|
|
|
|
}
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
<div style="page-break-after: always"></div>
|