|
|
|
|
|
## [$AcWing$ $1135$. 新年好](https://www.acwing.com/problem/content/1137/)
|
|
|
|
|
|
|
|
|
|
|
|
### 一、题目描述
|
|
|
|
|
|
重庆城里有 $n$ 个车站,$m$ 条 **双向** 公路连接其中的某些车站。
|
|
|
|
|
|
|
|
|
|
|
|
每两个车站 **最多** 用一条公路连接,从任何一个车站出发都可以经过一条或者多条公路到达其他车站,但不同的路径需要花费的时间可能不同。
|
|
|
|
|
|
|
|
|
|
|
|
在一条路径上花费的时间等于路径上所有公路需要的时间之和。
|
|
|
|
|
|
|
|
|
|
|
|
佳佳的家在车站 $1$,他有五个亲戚,分别住在车站 $a,b,c,d,e$。
|
|
|
|
|
|
|
|
|
|
|
|
过年了,他需要从自己的家出发,拜访每个亲戚(顺序任意),给他们送去节日的祝福。
|
|
|
|
|
|
|
|
|
|
|
|
怎样走,**才需要最少的时间**?
|
|
|
|
|
|
|
|
|
|
|
|
**输入格式**
|
|
|
|
|
|
第一行:包含两个整数 $n,m$,分别表示车站数目和公路数目。
|
|
|
|
|
|
|
|
|
|
|
|
第二行:包含五个整数 $a,b,c,d,e$,分别表示五个亲戚所在车站编号。
|
|
|
|
|
|
|
|
|
|
|
|
以下 $m$ 行,每行三个整数 $x,y,t$,表示公路连接的两个车站编号和时间。
|
|
|
|
|
|
|
|
|
|
|
|
**输出格式**
|
|
|
|
|
|
输出仅一行,包含一个整数 T,表示最少的总时间。
|
|
|
|
|
|
|
|
|
|
|
|
**数据范围**
|
|
|
|
|
|
$1≤n≤50000,1≤m≤10^5,1<a,b,c,d,e≤n,1≤x,y≤n,1≤t≤100$
|
|
|
|
|
|
|
|
|
|
|
|
**输入样例**:
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
6 6
|
|
|
|
|
|
2 3 4 5 6
|
|
|
|
|
|
1 2 8
|
|
|
|
|
|
2 3 3
|
|
|
|
|
|
3 4 4
|
|
|
|
|
|
4 5 5
|
|
|
|
|
|
5 6 2
|
|
|
|
|
|
1 6 7
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
输出样例:
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
21
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
### 二、解题思路
|
|
|
|
|
|
|
|
|
|
|
|
#### 1. 梳理概念
|
|
|
|
|
|
**车站**: $1,2,3,4,5,6,7,...,50000$,最多可能$50000$个
|
|
|
|
|
|
<font color='red' size=4><b>这个数量挺大</b></font>
|
|
|
|
|
|
|
|
|
|
|
|
**亲戚个数**:$5$个,分别住 $a,b,c,d,e$号车站
|
|
|
|
|
|
<font color='red' size=4><b>这个数量挺小,看来可以利用一下</b></font>
|
|
|
|
|
|
|
|
|
|
|
|
**亲戚家与车站关联关系**
|
|
|
|
|
|
$id[1]=8$ 表示第$1$个亲戚家住在$8$号车站附近,记录每个亲戚与车站的关系
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 2、思考过程
|
|
|
|
|
|
① 必须由佳佳的家出发,也就是出发点肯定是$1$号车站
|
|
|
|
|
|
② 现在想求佳佳去$5$个亲戚家,每一家都需要走到,不能漏掉任何一家,但顺序可以任意。这里要用一个关系数组$id[]$来把亲戚家的编号与车站号挂接一下。
|
|
|
|
|
|
③ 看到是最短路径问题,而且权值是正整数,考虑$Dijkstra$。
|
|
|
|
|
|
④ 但$Dijkstra$只能是单源最短路径求解,比如佳佳去二姨家,最短路径是多少。佳佳去三舅家,最短路径是多少。本题不是问某一家,问的是佳佳全去到,总的路径和最短是多少,这样的话,直接使用$Dijkstra$就无效了。
|
|
|
|
|
|
⑤ 继续思考:因为亲戚家只有$5$个,可以从这里下手,通过全排列的办法,枚举出所有的可能顺序,此时,计算次数=$5*4*3*2*1=120$次。
|
|
|
|
|
|
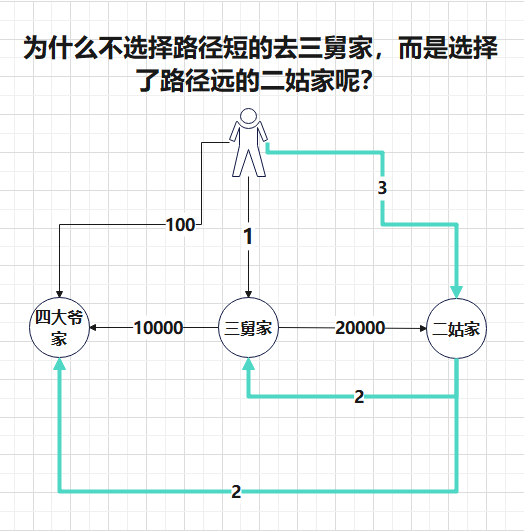
⑥ 跑多次$Dijkstra$是在干什么呢?就是在分别以二姨,三舅,四大爷家为出发点,分别计算出到其它亲戚家的最短距离,如果我们把顺序分别枚举出来,每次查一下已经预处理出来的两个亲戚家的最短距离,再加在一起,不就是可以进行$PK$最小值了吗?
|
|
|
|
|
|
|
|
|
|
|
|
至此,整体思路完成。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 3.编码步骤
|
|
|
|
|
|
|
|
|
|
|
|
* **$6$次最短路**
|
|
|
|
|
|
分别以佳佳家、五个亲戚家为出发点($id[i]~ i\in[0,5]$),求$6$次最短路,相当于打表,一会要查
|
|
|
|
|
|
|
|
|
|
|
|
* **求全排列**
|
|
|
|
|
|
因为佳佳所有的亲戚都要拜访到,现在不知道的是什么样顺序拜访才是时间最少的。 把所有可能顺序都 **枚举** 出来,通过查表,找出两个亲戚家之间的最小时间,累加结果的和,再$PK$最小就是答案
|
|
|
|
|
|
|
|
|
|
|
|
#### 4.实现细节
|
|
|
|
|
|
通过前面的$6$次打表预处理,可以求出$6$个$dist$数组,当我们需要查找 $1->5$的最短路径时,直接查$dist[1][5]$
|
|
|
|
|
|
|
|
|
|
|
|
$dist[i][j]$:从$i$号亲戚家(不是$i$号车站)出发,到达每个车站站点的 **最短距离**
|
|
|
|
|
|
|
|
|
|
|
|
<font color='red' size=4><b>注意:</b></font>
|
|
|
|
|
|
这两个维度在概念上这所以存在差异,本质上是为了防止$MLE$:
|
|
|
|
|
|
如果第一维也是车站站点的话,就是$50000*50000$的二维矩阵,$≈2.5e9$,大的吓人。因为我们只关心从这$6$个位置出发的所有最短距离,所以第一维开成$0$~$5$。现在的空间占用是 $50000*6=300000$,也就是$3e5$
|
|
|
|
|
|
|
|
|
|
|
|
$\large Code$
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
using namespace std;
|
|
|
|
|
|
|
|
|
|
|
|
typedef pair<int, int> PII;
|
|
|
|
|
|
|
|
|
|
|
|
const int N = 50010; // 车站数目
|
|
|
|
|
|
const int M = N << 1 << 1; // 公路数目,一般来说,N个节点,通常是2*N条边,如果是无向图,再乘2
|
|
|
|
|
|
const int INF = 0x3f3f3f3f;
|
|
|
|
|
|
|
|
|
|
|
|
int n, m; // 车站数目,公路数目
|
|
|
|
|
|
|
|
|
|
|
|
// 存图
|
|
|
|
|
|
int h[N], e[M], w[M], ne[M], idx;
|
|
|
|
|
|
void add(int a, int b, int c) {
|
|
|
|
|
|
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
|
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
|
|
int dis[6][N];
|
|
|
|
|
|
int id[6]; // 0号索引:佳佳的家,其它5个亲戚,分别下标为1~5,值为所在的车站编号
|
|
|
|
|
|
|
|
|
|
|
|
/*
|
|
|
|
|
|
1、用在Dijkstra中判断量不是出过队列,多次调用Dijkstra需要在函数体内进行状态重置
|
|
|
|
|
|
2、在dfs求全排列时,需要清空后记录在此路线上此 亲戚号 是不是走过了
|
|
|
|
|
|
*/
|
|
|
|
|
|
bool st[N];
|
|
|
|
|
|
|
|
|
|
|
|
/*
|
|
|
|
|
|
S:出发车站编号
|
|
|
|
|
|
dis[]:是全局变量dis[6][N]的某一个二维,其实是一个一维数组
|
|
|
|
|
|
C++的特点:如果数组做参数传递的话,将直接修改原地址的数据
|
|
|
|
|
|
此数组传值方式可以让我们深入理解C++的二维数组本质:就是多个一维数组,给数组头就可以顺序找到其它相关数据
|
|
|
|
|
|
计算的结果:获取到S出发到其它各个站点的最短距离,记录到dis[S][站点号]中
|
|
|
|
|
|
*/
|
|
|
|
|
|
void dijkstra(int S, int dis[]) {
|
|
|
|
|
|
dis[S] = 0;
|
|
|
|
|
|
memset(st, false, sizeof st);
|
|
|
|
|
|
priority_queue<PII, vector<PII>, greater<PII>> q;
|
|
|
|
|
|
q.push({0, S});
|
|
|
|
|
|
|
|
|
|
|
|
while (q.size()) {
|
|
|
|
|
|
auto t = q.top();
|
|
|
|
|
|
q.pop();
|
|
|
|
|
|
int u = t.second;
|
|
|
|
|
|
if (st[u]) continue;
|
|
|
|
|
|
st[u] = true;
|
|
|
|
|
|
for (int i = h[u]; ~i; i = ne[i]) {
|
|
|
|
|
|
int v = e[i];
|
|
|
|
|
|
if (dis[v] > dis[u] + w[i]) {
|
|
|
|
|
|
dis[v] = dis[u] + w[i];
|
|
|
|
|
|
q.push({dis[v], v});
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
|
|
int ans = INF; // 预求最小先设最大
|
|
|
|
|
|
|
|
|
|
|
|
// u:第几个亲戚
|
|
|
|
|
|
// pre:前序站点
|
|
|
|
|
|
// sum:按此路径走的总距离和
|
|
|
|
|
|
void dfs(int u, int pre, int sum) {
|
|
|
|
|
|
if (u == 6) { // 如果安排完所有亲戚的拜访顺序,就是得到了一组解,尝试更新最小值
|
|
|
|
|
|
ans = min(ans, sum);
|
|
|
|
|
|
return;
|
|
|
|
|
|
}
|
|
|
|
|
|
for (int i = 1; i <= 5; i++) // 在当前位置上,枚举每个可能出现在亲戚站点
|
|
|
|
|
|
if (!st[i]) { // 如果这个亲戚没走过
|
|
|
|
|
|
st[i] = true; // 走它
|
|
|
|
|
|
// 本位置填充完,下一个位置,需要传递前序是i,走过的路径和是sum+dis[pre][id[i]].因为提前打好表了,所以肯定是最小值,直接用就行了
|
|
|
|
|
|
// 需要注意的是一维是 6的上限,也就是 佳佳家+五个亲戚 ,而不是 车站号(佳佳家+五个亲戚) !因为这样的话,数据就很大,数组开起来麻烦,可能会MLE
|
|
|
|
|
|
// 要注意学习使用小的数据标号进行事情描述的思想
|
|
|
|
|
|
dfs(u + 1, i, sum + dis[pre][id[i]]);
|
|
|
|
|
|
st[i] = false; // 回溯
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
|
|
int main() {
|
|
|
|
|
|
scanf("%d %d", &n, &m); // 车站数目和公路数目
|
|
|
|
|
|
|
|
|
|
|
|
id[0] = 1; // 佳佳是0,id[0]=1,表示佳佳家在1号车站
|
|
|
|
|
|
for (int i = 1; i <= 5; i++) scanf("%d", &id[i]); // 五个亲戚所在车站编号,比如id[1]=2,描述1号亲戚在2号车站
|
|
|
|
|
|
|
|
|
|
|
|
// 建图完成后,图中的节点其实是 车站的站点编号,而不是亲戚编号
|
|
|
|
|
|
memset(h, -1, sizeof h); // 为了存图,需要初始化邻接表
|
|
|
|
|
|
|
|
|
|
|
|
while (m--) { // 建图
|
|
|
|
|
|
int a, b, c;
|
|
|
|
|
|
scanf("%d %d %d", &a, &b, &c); // a号车站到b号车站,需要走的时间是c
|
|
|
|
|
|
add(a, b, c), add(b, a, c); // 无向图,双向建边
|
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
|
|
// 计算从某个亲戚所在的车站出发,到达其它几个点的最短路径
|
|
|
|
|
|
// 因为这样会产生多组最短距离,需要一个二维的数组进行存储
|
|
|
|
|
|
memset(dis, 0x3f, sizeof dis);
|
|
|
|
|
|
for (int i = 0; i < 6; i++) dijkstra(id[i], dis[i]);
|
|
|
|
|
|
// 枚举每个亲戚所在的车站站点,多次Dijkstra,分别计算出以id[i]这个车站出发,到达其它点的最短距离,相当于打表
|
|
|
|
|
|
// 将结果距离保存到给定的二维数组dis的第二维中去,第一维是指从哪个车站点出发的意思
|
|
|
|
|
|
|
|
|
|
|
|
// dfs还要用这个st数组做其它用途,所以,需要再次的清空
|
|
|
|
|
|
memset(st, 0, sizeof st);
|
|
|
|
|
|
|
|
|
|
|
|
// 1:准备走第一家亲戚(具体是a,b,c,d,e哪一家随意都可以)
|
|
|
|
|
|
// 0:前序是佳佳自己家,他自己家的序号是0号
|
|
|
|
|
|
// 0:已经走过的最短距离和是0
|
|
|
|
|
|
dfs(1, 0, 0);
|
|
|
|
|
|
|
|
|
|
|
|
// 输出结果
|
|
|
|
|
|
printf("%d\n", ans);
|
|
|
|
|
|
return 0;
|
|
|
|
|
|
}
|
|
|
|
|
|
```
|