python/TangDou/AcWing/Tree/1075.md

##[$AcWing$ $1075$. 数字转换](https://www.acwing.com/problem/content/1077/)

### 一、题目描述
如果一个数 $x$ 的约数之和 $y$（不包括他本身）比他本身小，那么 $x$ 可以变成 $y$，$y$ 也可以变成 $x$。

例如，$4$ 可以变为 $3$，$1$ 可以变为 $7$。

限定所有数字变换在不超过 $n$ 的正整数范围内进行，**求不断进行数字变换且不出现重复数字的最多变换步数**。

**输入格式**
输入一个正整数 $n$。

**输出格式**
输出不断进行数字变换且不出现重复数字的最多变换步数。

**数据范围**
$1≤n≤50000$

**输入样例：**
```cpp {.line-numbers}
7
```

**输出样例：**
```cpp {.line-numbers}
3
```

**样例解释**
一种方案为：$4→3→1→7$。

### 二、筛法求约数和
**[求约数和的三重境界](https://www.cnblogs.com/littlehb/p/16650465.html)**

**普通筛法求约数和【类似于埃筛】**
```cpp {.line-numbers}
for (int i = 1; i <= n; i++)        //i是因数
    for (int j = 2; j <= n / i; j++)//j代表i的放大倍数
        sum[i * j] += i;            //i*j的约数和+i
```

### 三、建图
以 `n = 8` 为例建有向图，采用从 **约数和** 到 **原数** 方向建图。

**$Q:$为什么不创建双向边?**
$A$:小的数字往大的数字上连一条就够了,搜了根，这个树的直径就找出来了，没有反向搜的必要,维持一定的顺序就可以不用建双向边。

原本是要建双向边的，但是因为我每次$dfs$都是从根节点开始的，所以可以建有向边，因为有根树的直径一定会经过根节点。原本求树的直径要建无向边是因为不确定该点一定是根节点。 

**$Q$:为什么从小的数字往大的数字上连边就可以了，而从大的数字连边往小得数字连边就不行?**
$A$:一个数可能是多个数的约数之和,同时满足$sum[i]<i$。

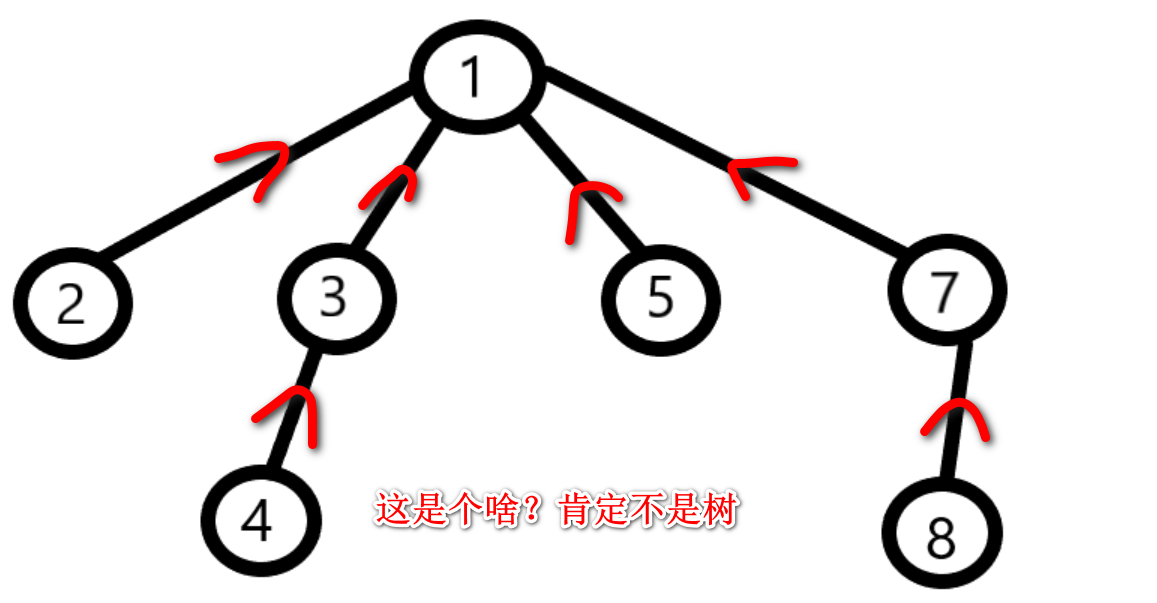
尝试一下反向建边，看看这是个啥:

![2.png](https://cdn.acwing.com/media/article/image/2022/09/03/64630_21e661462b-2.png) 


建好图后，本题就 **等价于** 找出一个森林中，**直径最长** 的树，并求出该树的 **直径**

**$Q$:建好的图中，是一棵树吗?**
**答**：不一定是树。比如$6$，它的约数和也是$6=1+2+3$，$sum[6]=6$,所以它是没有从约数和到自己的边的，而且，它也不是其它数字的约数和！它是一个孤立的点，性格比较怪异~,我们可以理解为创建的并不是一棵树，而是一个森林，森林中的某些树，可能也只有一个根节点。

![1.png](https://cdn.acwing.com/media/article/image/2022/09/03/64630_1e7119052b-1.png) 


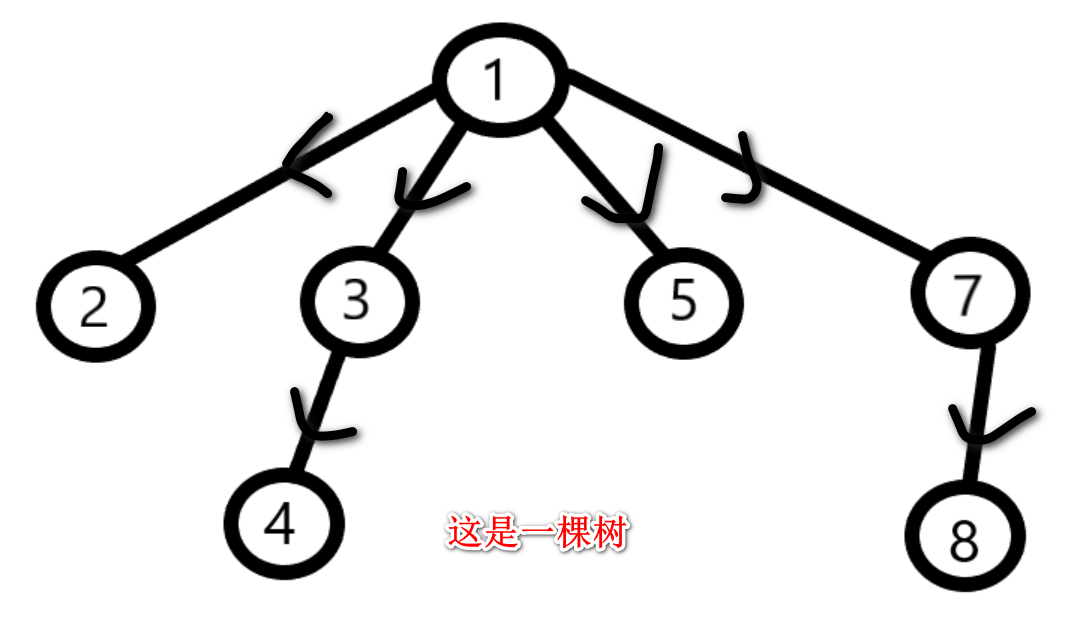
**$Q:$ 从$1$为根的树，为什么就是直径最长的树呢？**
看一下上面的图，只要想：任何的不包括$1$的中间环节加个$1$都不会矛盾的，反而能使结果加$1$，变得更好，所以找以$1$为根就可。这里没有给出严谨的数学证明，但对于小朋友而言，直白是不是更好理解？

### 四、算法步骤
① 预处理约数和
② 理解题意，手绘出图示关系。然后，创建以$1$为根的有向图。
③ 在图中，以$1$为根开始$dfs$，找出以$1$为根的子树中最长直径就是答案。

### 五、构建有向图求直径

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
const int N = 50010, M = N << 1;

int n;
int sum[N];
int d1[N], d2[N],  res;

// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

// 求树的直径模板
void dfs(int u) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        dfs(j);

        if (d1[j] + 1 >= d1[u]) {
            d2[u] = d1[u];
            d1[u] = d1[j] + 1;
        } else if (d1[j] + 1 > d2[u])
            d2[u] = d1[j] + 1;
    }
    res = max(res, d1[u] + d2[u]);
}

int main() {
    // 初始化
    memset(h, -1, sizeof h);
    cin >> n;

    // 筛法求约数和
    for (int i = 1; i <= n; i++)         // i是因数
        for (int j = 2; j <= n / i; j++) // j代表i的放大倍数 n/i不会溢出
            sum[i * j] += i;             // i*j的约数和+i

    for (int i = 1; i <= n; i++)
        // 当约数和小于原数，添加一条由约数和到原数的边，有向边.小数->大数存在边
        // 无环:目标是原数，一个原数不可能存在多个不同的约数和
        // 所以，这是一棵树
        if (sum[i] < i) add(sum[i], i);

    // 万物初始总有起点，1就是起点
    dfs(1);

    // 输出
    cout << res << endl;

    return 0;
}

```

### 六、理解与感悟
* $dfs$写法最好写成$void$返回，不要采用$int$方式，这样码风统一。此时，采用类似于记忆化的办法，利用数组$d1[N],d2[N]$来记录每个$u$结点最长距离和最短距离。~~采用$int$返回值时，还需要返回$d1$,太麻烦了~~。