python/TangDou/AcWing/StateCompression/292.md

##[$AcWing$ $292$. 炮兵阵地](https://www.acwing.com/problem/content/294/)

### 一、题目描述
司令部的将军们打算在 $N×M$ 的网格地图上部署他们的炮兵部队。

一个 $N×M$ 的地图由 $N$ 行 $M$ 列组成，地图的每一格可能是山地（用 $H$ 表示），也可能是平原（用 $P$ 表示），如下图。

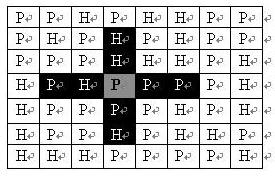
在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

![](https://www.acwing.com/media/article/image/2019/02/16/19_d512cdba31-1185_1.jpg)


如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。

**从图上可见炮兵的攻击范围不受地形的影响**。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（**保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内**），在整个地图区域内 **最多能够摆放多少我军的炮兵部队**。

**输入格式**
第一行包含两个由空格分割开的正整数，分别表示 $N$ 和 $M$；

接下来的 $N$ 行，每一行含有连续的 $M$ 个字符($P$ 或者 $H$)，中间没有空格。按顺序表示地图中每一行的数据。

**输出格式**
仅一行，包含一个整数 $K$，表示最多能摆放的炮兵部队的数量。

**数据范围**

$N≤100,M≤10$

**输入样例**：
```cpp {.line-numbers}
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
```

**输出样例**：
```cpp {.line-numbers}
6
```

### 二、题目解析

关于如何对状态进行 **二进制压缩**，在 **[玉米田【线性状压DP】](https://www.cnblogs.com/littlehb/p/15755261.html)** 有详细提及

关于如何**不同层不同合法状态判断**，在 **[小国王【线性状压DP】](https://www.cnblogs.com/littlehb/p/15752053.html)** 有详细提及

以上两点在本篇博客中不会再重复提及

观察到数据范围 $0<N≤100,0<M≤10$
故我们可以把 **行** 作为动态规划的阶段，然后对于第 **i** 行的摆放状态进行 **状态压缩**

这就变成了一道标准的 **线性状压DP**

因此在这两题里，我们只需压缩存储 **当前层的状态** ，然后枚举 **合法的上个阶段** 的状态进行 **转移** 即可


但是本题不同于 **小国王** 和 **玉米田**，这两题中棋子的 **攻击距离** 只有$1$,  玉米田比小国王麻烦些的是因为它有些玉米地是不育的，需要处理。


但是本题的棋子攻击范围是 $2$，我们只压缩当前层一层状态后进行转移，是不能保证该次转移是 **合法的**

即不能排除第 $i−2$ 层摆放的棋子可以攻击到第 $i$ 层棋子的 **不合法** 情况

而解决该问题的手段就是：**压缩存储两层的信息**，然后枚举合法的第 $i−2$ 层状态进行转移即可

#### 闫氏$DP$分析法

**状态表示**
- 集合 $f_{i,j,k}$: 考虑前 $i$ 层，且第 $i$ 层状态是 $j$，第 $i−1$ 层状态是 $k$ 的方案
- 属性 $f_{i,j,k}$: 该方案能够放置棋子的最大个数

**状态计算**—$f_{i,j,k}$:
$f_{i,j,k}$=$max(f_{i−1,k,pre}+cnt_j)$

其中$pre$是枚举的能够与 $k$ 和 $j$ 合法存在于三行中的所有状态

**初始状态**：$f_{0,0,0}$

**目标状态**：$f_{n,j,k}$(其中$j,k$枚举的是所有合法的相邻状态)
对于本题来说，直接开所有的状态空间，空间复杂度是 $O(N×2^M×2^M)$ 是会爆内存的

第一维上限是行数：$100$
第二维的状态是$2^M$，就是$2^{10}=1024$
第三维的状态是$2^M$，就是$2^{10}=1024$
所以三维数组的空间上限就是$100*1024*1024$,整数一个数位占$8$个$byte$，所以空间就是$8*100*1024*1024/1024/1024=800MB$，而本题要求最大空间上限$64MB$,所以开这么大的数组会$MLE$，需要在空间上进行优化。我们联想到其实第$i$层的情况只与第$i-1$层相关，所以可以使用滚动数组来优化。

果然，直接提交原始版本，系统提示： `Memory Limit Exceeded`

然后也可以预处理出来 **相邻行之间的合法转移**，也能避免掉一些不必要的不合法状态的枚举

### 三、朴素版本（$MLE$）
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 110;
const int M = 1 << 10;
int n, m; // n行m列，n<=100,m<=10,注意：状态压缩DP对列的长度很敏感，太大不行
int g[N]; // 记录每一列的山地情况，是一个二进制标识转化后的十进制数，最大就是全都是1，也就是2^m-1
int cnt[M];
int f[N][M][M];
vector<int> st;
vector<int> head[M];

// 检查一个状态是不是合法状态[同一行必须隔两个及两个以上才是安全的]
bool check(int x) {
    return !(x & x >> 1 || x & x >> 2);
}

// 统计某个状态中数字1的数量
int count(int s) {
    int res = 0;
    for (int i = 0; i < m; i++) // 遍历每一列
        if (s >> i & 1) res++;  // 如果此个位置数字是1，那么总的数量++
    return res;
}

int main() {
    // 输入
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++)       // n行
        for (int j = 1; j <= m; j++) { // m列
            char c;
            scanf(" %c", &c);                   // 注意scanf输入char的时候，前面要加一个空格
            if (c == 'H') g[i] += 1 << (j - 1); // 山地上不能够部署炮兵部队
        }
    // 1、预处理所有合法状态[单行合法即可]
    for (int i = 0; i < 1 << m; i++)
        if (check(i)) st.push_back(i), cnt[i] = count(i); // 预算出每个状态i里有多少个数位是1

    // 2、找出所有合法状态的合法转移[行间状态兼容检测]
    for (int a : st)
        for (int b : st)
            if (!(a & b)) // 上下行间不能存在同列的1
                head[a].push_back(b);
    // 3、dp
    for (int i = 1; i <= n; i++)      // 枚举每一行
        for (int a : st) {            // 枚举i行的每个状态
            if (g[i] & a) continue;   // 按i这样摆，确实是本行内不冲突，但如果准备放大炮的位置是高地，是不行的。
            for (int b : head[a])     // 枚举第i-1行的每个可能状态,b肯定与a不冲突
                for (int c : head[b]) // 枚举第i-2行的每个可能状态,c肯定是与b不冲突的
                    if (!(a & c))     // 如果c也与a不冲突的话,才是三行间完全兼容的方案
                        f[i][a][b] = max(f[i][a][b], f[i - 1][b][c] + cnt[a]);
        }

    // 4、枚举最终的状态最大值
    int res = 0;
    for (int a : st)
        for (int b : head[a])
            res = max(res, f[n][a][b]);

    // 5、输出
    printf("%d\n", res);
    return 0;
}
```
### 四、滚动数组优化版本
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 110;
const int M = 1 << 10;
int n, m;
int g[N];
int cnt[M];
int f[2][M][M];
vector<int> st;
vector<int> head[M];

bool check(int x) {
    return !(x & x >> 1 || x & x >> 2);
}

int count(int x) {
    int res = 0;
    while (x) {
        x = x & (x - 1);
        res++;
    }
    return res;
}

int main() {
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) {
            char c;
            scanf(" %c", &c);
            if (c == 'H') g[i] += 1 << (j - 1);
        }

    for (int i = 0; i < 1 << m; i++)
        if (check(i)) st.push_back(i), cnt[i] = count(i);

    for (int a : st)
        for (int b : st)
            if (!(a & b))
                head[a].push_back(b);

    for (int i = 1; i <= n; i++)
        for (int a : st) {
            if (g[i] & a) continue;
            for (int b : head[a])
                for (int c : head[b])
                    if (!(a & c))
                        f[i & 1][a][b] = max(f[i & 1][a][b], f[i - 1 & 1][b][c] + cnt[a]);
        }

    int res = 0;
    for (int a : st)
        for (int b : head[a])
            res = max(res, f[n & 1][a][b]);

    printf("%d\n", res);
    return 0;
}
```