python/TangDou/AcWing/SegmentTree/248.md

##[$AcWing$ $248$. 窗内的星星](https://www.acwing.com/problem/content/description/250/)

[洛谷题解](https://www.luogu.com.cn/problem/P1502)

### 一、题目描述
在一个天空中有很多星星（看作平面直角坐标系），已知每颗星星的坐标和亮度（都是整数）。

求用宽为 $W$、高为 $H$ 的矩形窗口（$W,H$ 为正整数） **能圈住的星星的亮度总和最大是多少**。（矩形边界上的星星不算）

**输入格式**
输入包含多组测试用例。

每个用例的第一行包含 $3$ 个整数：$n，W，H$，表示星星的数量，矩形窗口的宽和高。

然后是 $n$ 行，每行有 $3$ 个整数：$x，y，c，$ 表示每个星星的位置 $(x，y)$ 和亮度。

没有两颗星星在同一点上。

**输出格式**
每个测试用例输出一个亮度总和最大值。

每个结果占一行。

**数据范围**
$1≤n≤10000,\\
1≤W,H≤1000000,\\
0≤x,y<2^{31}$

**输入样例：**
```cpp {.line-numbers}
3 5 4
1 2 3
2 3 2
6 3 1

3 5 4
1 2 3
2 3 2
5 3 1
```

**输出样例：**
```cpp {.line-numbers}
5
6
```

### 二、解题思路
考虑把「**星星在窗子所在的矩形中**」转化为「**窗子的右上角在星星上面 $H$，右边 $W$ 的矩形中**」。这样就可以把整个问题转化为找一个点使得覆盖该点的矩形最多。

<center><img src='https://img2020.cnblogs.com/blog/1839956/202110/1839956-20211022113058631-151960196.png'></center>

（如图，矩形框住了两个星星）

现在考虑窗户边框的限制。

<center><img src='https://img2020.cnblogs.com/blog/1839956/202110/1839956-20211022113036159-344786121.png'></center>

如图，虽然窗户的右上角不能落在黑框上，只能落在黑框里，但将黑框的长和宽的两端都减小一个 $eps$（极小值）得到红框后，窗户的右上角就可以落在红框里的任何一个地方了。

但是如果减小 $eps$，星星所对应的矩形的坐标就变成了实数。

这时出现了一种方法，将矩形的长宽在两端都减小 $0.5$，然后把坐标轴向上平移、向右平移 $0.5$ 个单位。最后生成的矩形左下角是 $(x,y)$，右上角是 $x+W−1,y+H−1$。

这样做为什么是正确的呢？长宽减小的数值需要保证原本有交的矩形仍然有交。由于星星的坐标是整数，所以极限情况（可能会在矩形缩小后没有交的情况）如下图：

<center><img src='https://img2020.cnblogs.com/blog/1839956/202110/1839956-20211022113323427-1881509972.png'></center>

在减小 $0.5$ 之后仍然有交（只不过在对 $line$ 进行排序的时候需要把 $l$ 为正的排在前面）。而两端减小 $0.5$，合起来就是 $1$，这导致生成的矩形在平移坐标轴之后的坐标可以是整数。

所以这其实是一个很巧妙的方法，很多题解没说清楚。


于是我们可以将每个星星都扩展成一个矩形，这时我们注意到，若两个矩形之间有交集，他们便可以放在同一个窗户中。

如下图：

<center><img src='https://cdn.luogu.com.cn/upload/image_hosting/p295zpbp.png'></center>

图中灰色的部分就是两个星星构成的矩形的交集，只要窗户的右上角端点在灰色区域内，就能同时框住两个星星。

此时我们可以将问题转化为：平面上有若干个矩形，每个矩形都带有一个权值，求在哪个坐标上权值的总和最大。

接下来我们就可以使用扫描线来解决这个问题了，若当前星星的亮度值为$c$ ,则矩形的入边的权值设为 $1$ ，出边为 $-1$ ，此时我们只要求扫描线上的区间最大值即可得出答案，区间查询可以使用 `lazy_tag` 的方式实现。


**代码实现上的一些小细节：**

* 在对 $x$ 坐标进行升序排序时，将 $val$ 值按降序排序，这样才能处理两个矩形贴合的情况。
* 观察到 $0 \leq x_i,y_i \leq 2^{31}$, 所以我们需要将坐标进行离散化处理。



### 三、问题集
请问一下 样例中第二个答案是$6$也就是三个星星都能框进去 而数据是这样的:
```cpp {.line-numbers}
3 5 4
1 2 3
2 3 2
5 3 1
```
最左边的点是($1,2$)最右边的点是($5,3$)
那么想要把这两个同时框进去不是需要至少宽度是$6$嘛也就是从$0$框到$6$
可样例中宽度是$5$ 那么应该会有一个点卡在边界上那么不就不能算是有贡献了嘛?

**$yxc$回复：**
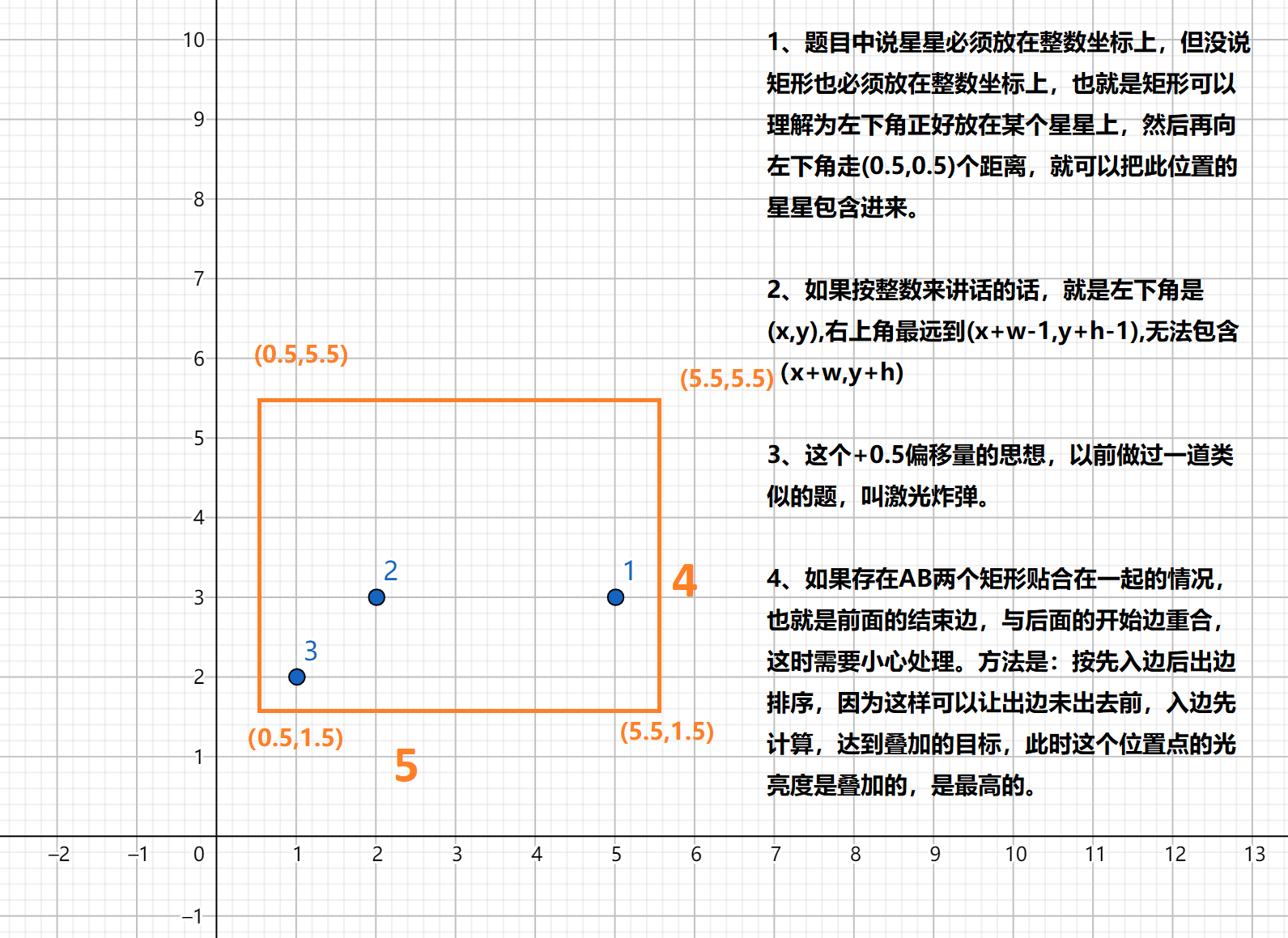
从$0.5$到$5.5$的框就可以啦，所以宽度是$5$的话可以同时包含$(1, 2)$和$(5, 3)$
它只是要求星星在整点上,但是我框的矩形顶点是不用在整点上的,所以我们可以平移$0.5$这样就能多框一段了。

![](http://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/2022/12/426de2cba8a28915673f776c6bdc8974.png)

### 四、实现代码
```cpp {.line-numbers}
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <vector>

using namespace std;
typedef long long LL;
const int N = 10010;

//在对 x 坐标进行升序排序时，将 k 值按降序排序，这样才能处理两个矩形贴合的情况
struct Seg {
    LL x, y1, y2, c;
    bool operator<(const Seg &t) const {
        if (x == t.x) return c > t.c; // 1在前，-1在后，先处理入边再处理出边
        return x < t.x;
    }
} seg[N << 1];

struct Node {
    int l, r;
    int maxc, add;
} tr[N << 3];

int n, w, h;
vector<LL> ys;

void pushup(int u) {
    tr[u].maxc = max(tr[u << 1].maxc, tr[u << 1 | 1].maxc);
}

void build(int u, int l, int r) {
    tr[u] = {l, r, 0, 0};
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
}

void pushdown(int u) {
    if (tr[u].add) {
        tr[u << 1].maxc += tr[u].add;
        tr[u << 1].add += tr[u].add;
        tr[u << 1 | 1].maxc += tr[u].add;
        tr[u << 1 | 1].add += tr[u].add;
        tr[u].add = 0;
    }
}

void modify(int u, int l, int r, int c) {
    if (l <= tr[u].l && tr[u].r <= r) {
        tr[u].maxc += c;
        tr[u].add += c;
        return;
    }

    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    if (l <= mid) modify(u << 1, l, r, c);
    if (r > mid) modify(u << 1 | 1, l, r, c);

    pushup(u);
}

int find(LL x) {
    return lower_bound(ys.begin(), ys.end(), x) - ys.begin();
}

int main() {
    //加快读入
    ios::sync_with_stdio(false), cin.tie(0);

    while (cin >> n >> w >> h) {
        ys.clear();
        for (int i = 1; i <= n; i++) {
            LL x, y;
            int c;
            cin >> x >> y >> c;
            //区别在这里！
            /*
            需配合：
            if (x == t.x) return c > t.c; // 1在前，-1在后，先处理入边再处理出边
            */
            seg[2 * i - 1] = {x, y, y + h - 1, c};
            //此处,x+w-1,注意：多减了一个1~
            seg[2 * i] = {x + w - 1, y, y + h - 1, -c};
            ys.push_back(y), ys.push_back(y + h - 1);
        }

        sort(ys.begin(), ys.end());
        ys.erase(unique(ys.begin(), ys.end()), ys.end());

        sort(seg + 1, seg + 1 + 2 * n);

        build(1, 0, ys.size() - 1);

        int res = 0;
        for (int i = 1; i <= 2 * n; i++) {
            res = max(res, tr[1].maxc);
            modify(1, find(seg[i].y1), find(seg[i].y2), seg[i].c);
        }
        printf("%d\n", res);
    }
    return 0;
}
```