python/TangDou/AcWing/PrefixAndDifference/一维差分和二维差分.md

### [$AcWing$ $797$. 差分](https://www.acwing.com/problem/content/799/)

定义：$b[i]=a[i]-a[i-1]$,称$b$数组是$a$数组的差分数组。

举个栗子：

$a=[0,1,2,3,4,5]$

$b=[0,1,1,1,1,1]$ 

为啥呢？
$a[5]-a[4]=b[5]$
$a[4]-a[3]=b[4]$
$a[3]-a[2]=b[3]$
$a[2]-a[1]=b[2]$
$a[1]-a[0]=b[1]$

算一下，就是$b=[1,1,1,1,1]$

把上面五个式子左边加在一起，右边也加在一起，两边还应该相等。就是：
$a[5]-a[4]+a[4]-a[3]+a[3]-a[2]+a[2]-a[1]+a[1]-a[0]=b[5]+b[4]+b[3]+b[2]+b[1]$

$a[5]=b[1]+b[2]+b[3]+b[4]+b[5]$

太奇妙了！<font color='red'>**$a$数组是$b$数组的一维前缀和数组！**</font>

**小结：**
(1)、$a$数组中，每个数字**后面减前面得到的数字填入$b$数组**，$b$数组就叫$a$数组的差分数组。

(2)、同时，$a$数组就是$b$数组的前缀和数组。

(3)、**通过“叠加”差分数组，就可以还原出“原数组”的每一个数字！**

(4)、**前缀和与差分互为逆运算，有原数组可以计算出差分数组；有差分数组，也可以还原成原数组。**

#### 2、一维差分作用

使用场景：

 **在某个区间$[l,r]$的多次操作都加上（或减去）一个数$x$时，一维差分可以大大提高运算速度。**

举个栗子：

<center><img src='https://img2020.cnblogs.com/blog/8562/202109/8562-20210907140423790-882246210.png'></center>

总结公式：

```c++
void insert(int l,int r,int c){
    b[l]+=c;
    b[r+1]-=c;
}
```

我们利用刚才的结论:**通过“叠加”差分数组，就可以还原出“原数组”的每一个数字！**!这玩意就整一回合适吗？不合适，还不够费功夫的呢！生成一维差分也就算了，从一维差分数组还原回原数组就需要$n$次运算，整不好还赔了呢！但如果是多次区间加减运算，就合适了！


#### 3、一维差分应用
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 100010;
int n, m;
int a[N], b[N];

/**
 * 功能：差分计算
 * @param l 左边界
 * @param r 右边界
 * @param c 值
 */
void insert(int l, int r, int c) {
    b[l] += c;
    b[r + 1] -= c;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        insert(i, i, a[i]);
        //或者 b[i]=a[i]-a[i-1];
  }

    while (m--) {
        int l, r, c;
        cin >> l >> r >> c;
        insert(l, r, c);
    }

    for (int i = 1; i <= n; i++)
        a[i] = a[i - 1] + b[i], printf("%d ", a[i]);
    return 0;
}
```


### [$AcWing$ $798$. 差分矩阵](https://www.acwing.com/problem/content/800/)

#### 1、二维差分定义
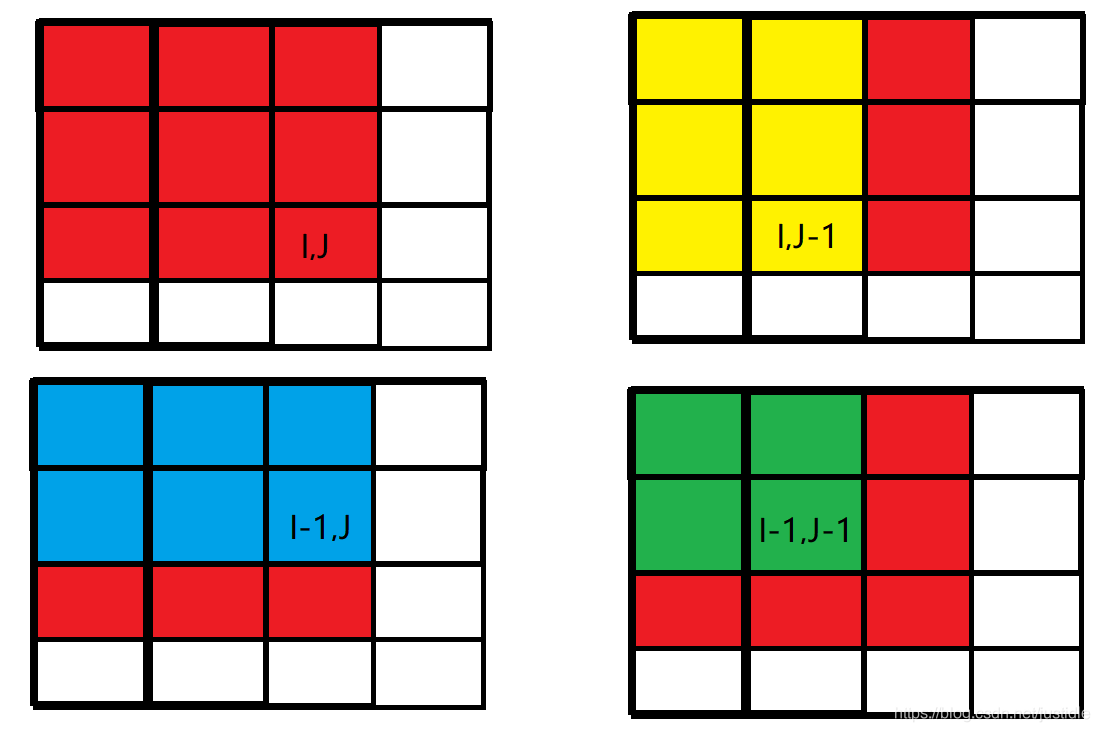
我们有一个矩阵，如下图所示。
![](https://img2020.cnblogs.com/blog/8562/202109/8562-20210907141102465-1061848020.png)

根据二维前缀和表示的是右上角矩形的和，由于差分只涉及前面相邻的数（由一维可以推出），并且由前面范围的数相加得到这个位置的数。那么类比二维前缀和和一维差分，可以简单推测出

**二维差分的公式**
$b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]$


**如何从差分矩阵得到原矩阵呢？**[就是二维前缀和公式]
$a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j]$

**举个栗子**
比如，我们有一个矩阵 a，如下所示：
```c++
1 2 4 3
5 1 2 4
6 3 5 9
```
那么对应的二维差分矩阵 b 如下：
```c++
1  1  2 -1
4 -5 -1  3
1  1  1  2
```
#### 2、二维差分用途
和一维差分的用途基本一致，在一个二维矩阵中，有多块区间需要增加或减少一个数值，多次操作后求最终的矩阵内容。如果按照传统办法，就是二层循环，复杂度很高，如果预处理出一个二维的差分矩阵，以后的多轮操作都转为了4次加加减减操作，可以视为$O(1)$级别的时间复杂度，运算效率将得到极大提高。

#### 3、二维差分构建
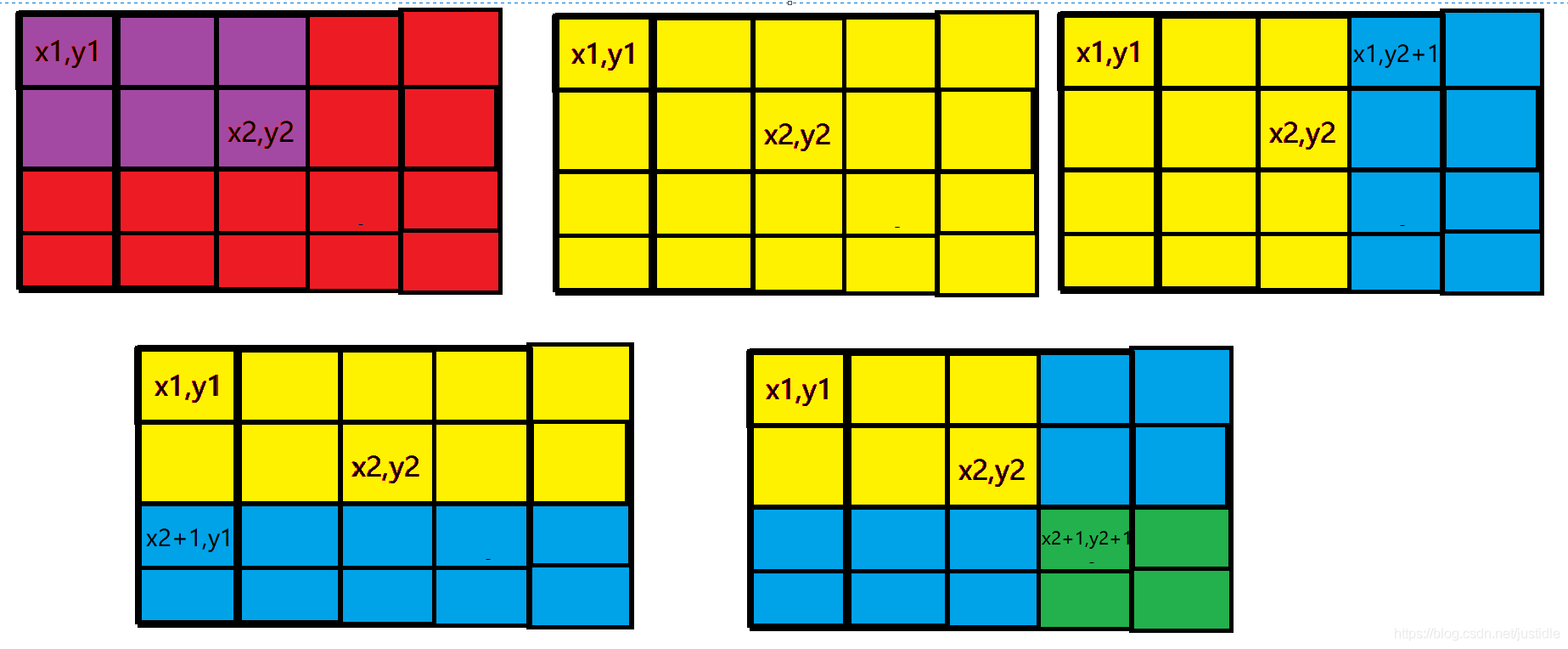
如果我们要在左上角是 `(x1,y1)`，右下角是 `(x2,y2)` 的矩形区间每个值都 `+c`，如下图所示
![1.png](https://cdn.acwing.com/media/article/image/2021/04/07/64630_88b316d097-1.png) 
在我们要的区间开始位置`（x1,y1）`处 `+c`，根据前缀和的性质，那么它影响的就是整个黄色部分，多影响了两个蓝色部分，所以在两个蓝色部分 `-c` 消除 `+c` 的影响，而两个蓝色部分重叠的绿色部分多了个 `-c` 的影响，所以绿色部分 `+c` 消除影响。所以对应的计算方法如下：
```
void insert(int x1, int y1, int x2, int y2, int c){
    b[x1][y1] += c;             //开始位置增加C
    b[x2 + 1][y1] -= c;         //见上面的图，把第二行的蓝色区域减去C
    b[x1][y2 + 1] -= c;         //见上面的图，把第一行的蓝色区域减去C
    b[x2 + 1][y2 + 1] += c;     //交叉位置被减了两次，需要补回来。
}
```
#### 4、二维差分应用

```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
int a[N][N], b[N][N];
int n, m, q;

/**
 * 功能：二维差分构建
 * @param x1 左上角横坐标
 * @param y1 左上角纵坐标
 * @param x2 右下角横坐标
 * @param y2 右下角纵坐标
 * @param c  值
 */
void insert(int x1, int y1, int x2, int y2, int c) {
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main() {
    cin >> n >> m >> q;
    //读入并构建
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j], insert(i, j, i, j, a[i][j]);

    //q次区域变化
    while (q--) {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }
    
    //还原二维数组
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {//二维前缀和公式
            a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];
            printf("%d ", a[i][j]);
        }
        printf("\n");
    }
    return 0;
}
```