|
|
|
|
|
### 一、一维前缀和
|
|
|
|
|
|
|
|
|
|
|
|
场景模拟:
|
|
|
|
|
|
|
|
|
|
|
|
老师让 **班长糖豆** 帮着计算一下全班同学语文考试的总分,老师负责读每个同学的分数,糖豆负责计算。
|
|
|
|
|
|
|
|
|
|
|
|
老师:“第一名,张三 $100$分”, 糖豆记录如下:$100$分
|
|
|
|
|
|
老师:“第二名,李四 $99$分”, 糖豆 **擦去** $100$,修改为:$199$分
|
|
|
|
|
|
老师:“第三名,王五 $98$分”, 糖豆 **擦去** $199$,修改为:$297$分
|
|
|
|
|
|
...
|
|
|
|
|
|
老师:“第四十五名,赵九 $60$分”, 糖豆 **擦去** $4179$,修改为:$4239$分
|
|
|
|
|
|
|
|
|
|
|
|
完事了,糖豆汇报总分:“$4239$分!任务结束!”
|
|
|
|
|
|
|
|
|
|
|
|
老师想了一想,问了一句:“那前十名共多少分?”
|
|
|
|
|
|
|
|
|
|
|
|
糖豆有点懵,因为把前十位的结果已经擦去啦!只能让老师从第一名开始到第十名再读一次。^_^
|
|
|
|
|
|
|
|
|
|
|
|
老师又想问:"那前二十名共多少分?"
|
|
|
|
|
|
|
|
|
|
|
|
糖豆彻底懵了,只能让老师从第一名开始到第二十名再读一次。^_^
|
|
|
|
|
|
|
|
|
|
|
|
老师也疯了!!!
|
|
|
|
|
|
|
|
|
|
|
|
看来这个办法不太行,老师的需求总变化!
|
|
|
|
|
|
|
|
|
|
|
|
那有什么办法呢??糖豆会有办法的:
|
|
|
|
|
|
|
|
|
|
|
|
<font color='red'>记录前$i$个同学的分数总和!不擦!</font>
|
|
|
|
|
|
|
|
|
|
|
|
来吧,老师,你说你想要啥?
|
|
|
|
|
|
|
|
|
|
|
|
我想要前$20$名的分数总和!没问题,我记的就是这个,给你!
|
|
|
|
|
|
|
|
|
|
|
|
我想要$20$至$30$名的分数总和!啊???还想这么要?怎么办呢?
|
|
|
|
|
|
|
|
|
|
|
|
我们用数学的公式来描述一下,这样方便说明:
|
|
|
|
|
|
|
|
|
|
|
|
$a[i]$代表$i$号同学分数,$s[i]$代表$i$号同学及他以前的所有同学的分数总和。
|
|
|
|
|
|
|
|
|
|
|
|
那么有下面的关系式:
|
|
|
|
|
|
$s[i-1]=a[1]+a[2]+a[3]+...+a[i-1]$ ①
|
|
|
|
|
|
|
|
|
|
|
|
$s[i]=\ \ \ \ \ \ \ a[1]+a[2]+a[3]+...+a[i-1]+a[i]$ ②
|
|
|
|
|
|
|
|
|
|
|
|
将①式代入②式,得到
|
|
|
|
|
|
$s[i]=s[i-1]+a[i]$ ③
|
|
|
|
|
|
|
|
|
|
|
|
如果记录了这个$s[i]$,就能回答好多的问题:
|
|
|
|
|
|
|
|
|
|
|
|
1、第$5$名同学的分数是多少?
|
|
|
|
|
|
答:$s[5]-s[4]$ ,为啥呢?因为③式的变形 $a[i]=s[i]-s[i-1]$
|
|
|
|
|
|
|
|
|
|
|
|
2、第$1$名到第$10$名同学的分数和是多少?
|
|
|
|
|
|
答:$s[10]$ 为啥呢?因为前缀和定义就是从`1`到`i`的数据和嘛。
|
|
|
|
|
|
|
|
|
|
|
|
3、第$5$名到第$10$名同学的分数和是多少?
|
|
|
|
|
|
答:$s[10]-s[4]$
|
|
|
|
|
|
|
|
|
|
|
|
为啥呢?
|
|
|
|
|
|
其实我们想求的是:$a[5]+a[6]+a[7]+a[8]+a[9]+a[10]$
|
|
|
|
|
|
我们使用$s[i]$来构建上面的式子:
|
|
|
|
|
|
|
|
|
|
|
|
$s[4]=a[1]+a[2]+a[3]+a[4]$ ①
|
|
|
|
|
|
|
|
|
|
|
|
$s[10]=a[1]+a[2]+a[3]+a[4]+a[5]+...+a[10]$ ②
|
|
|
|
|
|
|
|
|
|
|
|
将①式代入②式,就是$s[10]=s[4]+a[5]+a[6]+a[7]+a[8]+a[9]+a[10]$
|
|
|
|
|
|
|
|
|
|
|
|
移项得到:$s[10]-s[4]=a[5]+a[6]+a[7]+a[8]+a[9]+a[10]$
|
|
|
|
|
|
|
|
|
|
|
|
<font color='red'>注意:
|
|
|
|
|
|
前缀和一般从数下标$1$开始,这是因为它的定义是$s[i]=s[i-1]+a[i]$,如果$i$从$0$开始,$s$数组下标就会出现负数,这样还需一堆$if$判断,麻烦,所以,一般为了代码简单,我们都把$a[0]=0$,通常在全局变量区域里定义$a$数组,这样连$a[0]=0$也省略了,$s[0]$其实也是定义在全局变量区域的,所以$s[0]=0$,这样操作代码就简单了。
|
|
|
|
|
|
</font>
|
|
|
|
|
|
|
|
|
|
|
|
#### 1. 使用场景
|
|
|
|
|
|
给定一个原始数组,后面需要多次查询某一个的数值和,比如 $1$ $2$ $3$ $4$ $6$ $3$ $7$ $8$ $9$ $10$,$10$个数字,需要问$N$次,每次问从`x`到`y`的位置,相加的和是几。
|
|
|
|
|
|
|
|
|
|
|
|
如果按普通想法,就是每问一次就计算一次,不利用以前的结果。这样假设每次的`l`到`r`的距离是`m`,很显然,共需要`m*N`次操作,如果使用了前缀和的预处理,计算一次前缀和,就是`N`次运算,得到一个结果数组`s[N]`,以后每次查询都是 $s[r]-s[l-1]$,就是一次运算,快了很多。
|
|
|
|
|
|
|
|
|
|
|
|
####[$AcWing$ $795$. 前缀和](https://www.acwing.com/problem/content/797/)
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
|
|
|
|
|
|
using namespace std;
|
|
|
|
|
|
const int N = 100010;
|
|
|
|
|
|
int q[N];
|
|
|
|
|
|
int s[N];
|
|
|
|
|
|
|
|
|
|
|
|
//一维前缀和
|
|
|
|
|
|
int main() {
|
|
|
|
|
|
int n, m;
|
|
|
|
|
|
cin >> n >> m;
|
|
|
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
|
|
|
cin >> q[i];
|
|
|
|
|
|
s[i] = s[i - 1] + q[i];
|
|
|
|
|
|
}
|
|
|
|
|
|
while (m--) {
|
|
|
|
|
|
int l, r;
|
|
|
|
|
|
cin >> l >> r;
|
|
|
|
|
|
printf("%d\n", s[r] - s[l - 1]);
|
|
|
|
|
|
}
|
|
|
|
|
|
return 0;
|
|
|
|
|
|
}
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
###[$AcWing$ $796$. 子矩阵的和](https://www.acwing.com/problem/content/798/)
|
|
|
|
|
|
|
|
|
|
|
|
**什么是二维前缀和?**
|
|
|
|
|
|
|
|
|
|
|
|
`a[N][M]`假设为原数组,`s[N][M]`为二维前缀和数组,`s[i][j]`的意义是:原数组前`i`行,前`j`列的数组元素值的和。
|
|
|
|
|
|
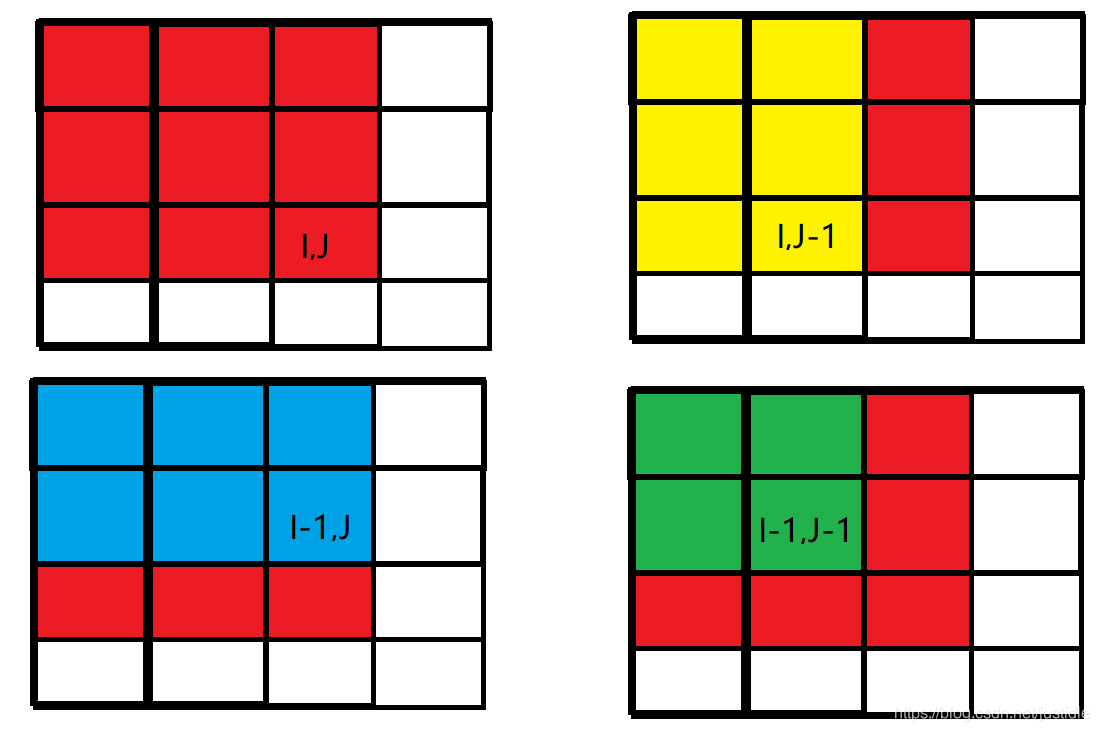
说白了,就是`1->i`行,`1->j`列的所有元素值的和,就是左上角的格子内容和:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
本质上和一维前缀和是一个意思,一维是第`1`个元素到第`n`个元素的累加和,二维是从左上角到`(i,j)`的累加和。
|
|
|
|
|
|
|
|
|
|
|
|
#### 1、公式的推导
|
|
|
|
|
|
$s[3][3]=a[1][1]+a[1][2]+a[1][3]$
|
|
|
|
|
|
$\ \ \ \ \ \ \ \ \ \ +a[2][1]+a[2][2]+a[2][3]$
|
|
|
|
|
|
$\ \ \ \ \ \ \ \ \ \ +a[3][1]+a[3][2]+a[3][3]$
|
|
|
|
|
|
|
|
|
|
|
|
$s[3][2]=a[1][1]+a[1][2]$
|
|
|
|
|
|
$\ \ \ \ \ \ \ \ \ \ +a[2][1]+a[2][2]$
|
|
|
|
|
|
$\ \ \ \ \ \ \ \ \ \ +a[3][1]+a[3][2]$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
$s[2][3]=a[1][1]+a[1][2]+a[1][3]$
|
|
|
|
|
|
$\ \ \ \ \ \ \ \ \ \ +a[2][1]+a[2][2]+a[2][3]$
|
|
|
|
|
|
|
|
|
|
|
|
$s[2][2]=a[1][1]+a[1][2]$
|
|
|
|
|
|
$\ \ \ \ \ \ \ \ \ \ +a[2][1]+a[2][2]$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
观察上面4个式子,我们想要计算$s[3][3]$,还不想用笨办法,一个个用$a[i][j]$来累加出来,就可以利用已经算出来的结果值进行运算获得!
|
|
|
|
|
|
|
|
|
|
|
|
$s[3][3]=s[3][2]+s[2][3]-s[2][2]+a[3][3]$
|
|
|
|
|
|
|
|
|
|
|
|
抽象一下,就是:(如果感觉看代数式子不好理解,就用上面图理解就行啦!)
|
|
|
|
|
|
|
|
|
|
|
|
$s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]$
|
|
|
|
|
|
|
|
|
|
|
|
#### 2、计算子区域的前缀和
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 3、C++ 代码
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
|
|
|
|
|
|
using namespace std;
|
|
|
|
|
|
const int N = 1010;
|
|
|
|
|
|
int a[N][N];
|
|
|
|
|
|
int s[N][N];
|
|
|
|
|
|
|
|
|
|
|
|
int main() {
|
|
|
|
|
|
int n, m, q;
|
|
|
|
|
|
cin >> n >> m >> q;
|
|
|
|
|
|
for (int i = 1; i <= n; i++)
|
|
|
|
|
|
for (int j = 1; j <= m; j++) {
|
|
|
|
|
|
cin >> a[i][j];
|
|
|
|
|
|
s[i][j] = s[i - 1][j] + s[i][j - 1] + a[i][j] - s[i - 1][j - 1];
|
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
|
|
while (q--) {
|
|
|
|
|
|
int x1, y1, x2, y2;
|
|
|
|
|
|
cin >> x1 >> y1 >> x2 >> y2;
|
|
|
|
|
|
printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
|
|
|
|
|
|
}
|
|
|
|
|
|
return 0;
|
|
|
|
|
|
}
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
#### 练习题
|
|
|
|
|
|
**[(一维前缀和) 洛谷 $P1614$ 爱与愁的心痛](https://blog.csdn.net/m0_50683128/article/details/110673195)**
|
|
|
|
|
|
|
|
|
|
|
|
**[前缀和和差分洛谷题单总结](https://blog.csdn.net/piqihaoshaonian/article/details/127515000)**
|