|
|
|
|
|
##[$AcWing$ $841$. 字符串哈希](https://www.acwing.com/problem/content/843/)
|
|
|
|
|
|
|
|
|
|
|
|
### 一、题目描述
|
|
|
|
|
|
|
|
|
|
|
|
给定一个长度为 $n$ 的字符串,再给定 $m$ 个询问,每个询问包含四个整数 $l_1,r_1,l_2,r_2$,请你判断 $[l_1,r_1]$ 和 $[l_2,r_2]$ 这两个区间所包含的字符串子串是否完全相同。
|
|
|
|
|
|
|
|
|
|
|
|
字符串中只包含大小写英文字母和数字。
|
|
|
|
|
|
|
|
|
|
|
|
**输入格式**
|
|
|
|
|
|
第一行包含整数 $n$ 和 $m$,表示字符串长度和询问次数。
|
|
|
|
|
|
|
|
|
|
|
|
第二行包含一个长度为 $n$ 的字符串,字符串中只包含大小写英文字母和数字。
|
|
|
|
|
|
|
|
|
|
|
|
接下来 $m$ 行,每行包含四个整数 $l_1,r_1,l_2,r_2$,表示一次询问所涉及的两个区间。
|
|
|
|
|
|
|
|
|
|
|
|
注意,字符串的位置从 $1$ 开始编号。
|
|
|
|
|
|
|
|
|
|
|
|
**输出格式**
|
|
|
|
|
|
对于每个询问输出一个结果,如果两个字符串子串完全相同则输出 `Yes`,否则输出 `No`。
|
|
|
|
|
|
|
|
|
|
|
|
每个结果占一行。
|
|
|
|
|
|
|
|
|
|
|
|
**数据范围**
|
|
|
|
|
|
$1≤n,m≤10^5$
|
|
|
|
|
|
|
|
|
|
|
|
**输入样例:**
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
8 3
|
|
|
|
|
|
aabbaabb
|
|
|
|
|
|
1 3 5 7
|
|
|
|
|
|
1 3 6 8
|
|
|
|
|
|
1 2 1 2
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
**输出样例:**
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
Yes
|
|
|
|
|
|
No
|
|
|
|
|
|
Yes
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
### 二、算法思路
|
|
|
|
|
|
字符串哈希 $O(n+m)$
|
|
|
|
|
|
|
|
|
|
|
|
全称 **字符串前缀哈希法**,把字符串变成一个$p$进制数字(哈希值),实现不同的字符串映射到不同的数字。并且,用$h[N]$记录字符串前$N$个字符的$Hash$值,类似于前缀和。
|
|
|
|
|
|
|
|
|
|
|
|
作用就是把$O(N)$的时间复杂度降为$O(1)$。比如本题就是对比任意两段内字符串是不是相同,正常就是类似于一个循环长度次的$substr$,其实用$hash$差就能一步搞定!
|
|
|
|
|
|
|
|
|
|
|
|
**举个栗子**:
|
|
|
|
|
|
```c++
|
|
|
|
|
|
str="ABCABCDEYXCACWING";
|
|
|
|
|
|
h[0]=0;
|
|
|
|
|
|
h[1]="A"的Hash值;
|
|
|
|
|
|
h[2]="AB"的Hash值;
|
|
|
|
|
|
h[3]="ABC"的Hash值;
|
|
|
|
|
|
h[4]="ABCA"的Hash值;
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
对形如$X_1X_2X_3...X_{n-1}X_n$的字符串,采用字符 $ASCII$码乘上$P$次方来计算哈希值。
|
|
|
|
|
|
|
|
|
|
|
|
映射公式:$(X_1 \times P^{n-1} +X_2 \times P^{n-2}+...+X_{n-1}\times P^1 + X_n \times P^0) mod \ Q$
|
|
|
|
|
|
|
|
|
|
|
|
比如:字符串$ABCD$,$P=131$
|
|
|
|
|
|
那么$h[4]=65*131^3+66*131^2+67*131^1+68*131^0$
|
|
|
|
|
|
|
|
|
|
|
|
而$AB$,$P=131$
|
|
|
|
|
|
说是$h[2]=65*131^1+66*131^0$
|
|
|
|
|
|
|
|
|
|
|
|
我们想要求"$CD$"的$HASH$值,怎么求呢?
|
|
|
|
|
|
就是 $h[4]-h[2]*131^2$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 注意
|
|
|
|
|
|
|
|
|
|
|
|
1. 任意字符不可以映射成$0$,否则会出现不同的字符串都映射成$0$的情况,比如$A$,$AA$,$AAA$皆为$0$
|
|
|
|
|
|
|
|
|
|
|
|
2. 冲突问题:通过巧妙设置$P$($131$或$13331$) ,$Q$($2^{64}$)的值,一般可以**理解为不产生冲突**(玄学)。
|
|
|
|
|
|
|
|
|
|
|
|
$Q=2^{64}$这个取模动作在代码中没有出现过,这是因为采用了$unsinged \ long\ long $,它本身就是$2^{64}$,如果超过了这个数字,就直接自动溢出,起到了取模的作用。
|
|
|
|
|
|
|
|
|
|
|
|
问题是比较不同区间的子串是否相同,就转化为对应的哈希值是否相同。
|
|
|
|
|
|
|
|
|
|
|
|
求一个字符串的哈希值就类似于构建一维前缀和,求一个字符串的子串哈希值就相当于一维前缀和应用:
|
|
|
|
|
|
|
|
|
|
|
|
构建: $h[i]=h[i-1] \times P+s[i-1] \ \ \ i∈[1,n]$ $h$为前缀和数组,$s[i-1]$为字符串数组此位置字符对应的$ASCII$码。
|
|
|
|
|
|
|
|
|
|
|
|
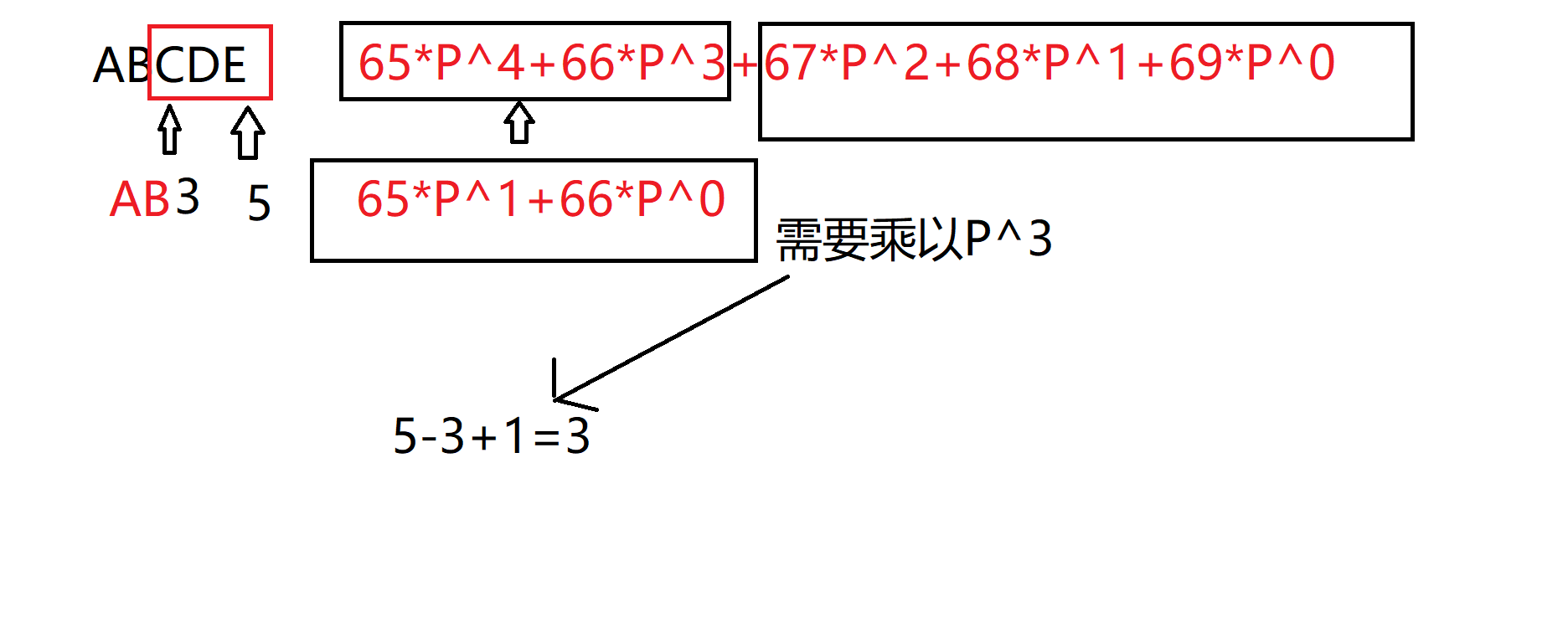
应用: 查询$l,r$之间部分字符串的$hash=h[r]−h[l−1]×P^{r−l+1}$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
### 三、实现代码
|
|
|
|
|
|
```cpp {.line-numbers}
|
|
|
|
|
|
#include <bits/stdc++.h>
|
|
|
|
|
|
|
|
|
|
|
|
using namespace std;
|
|
|
|
|
|
typedef unsigned long long ULL;
|
|
|
|
|
|
|
|
|
|
|
|
const int N = 100010;
|
|
|
|
|
|
const int P = 131;
|
|
|
|
|
|
int n, m;
|
|
|
|
|
|
string str;
|
|
|
|
|
|
ULL h[N], p[N];
|
|
|
|
|
|
ULL get(int l, int r) {
|
|
|
|
|
|
return h[r] - h[l - 1] * p[r - l + 1];
|
|
|
|
|
|
}
|
|
|
|
|
|
int main() {
|
|
|
|
|
|
cin >> n >> m >> str;
|
|
|
|
|
|
p[0] = 1; // p^0=1,初始化
|
|
|
|
|
|
for (int i = 1; i <= n; i++) {
|
|
|
|
|
|
p[i] = p[i - 1] * P; // 基数
|
|
|
|
|
|
h[i] = h[i - 1] * P + str[i - 1]; // 前缀和
|
|
|
|
|
|
}
|
|
|
|
|
|
while (m--) {
|
|
|
|
|
|
int l1, r1, l2, r2;
|
|
|
|
|
|
cin >> l1 >> r1 >> l2 >> r2;
|
|
|
|
|
|
if (get(l1, r1) == get(l2, r2))
|
|
|
|
|
|
puts("Yes");
|
|
|
|
|
|
else
|
|
|
|
|
|
puts("No");
|
|
|
|
|
|
}
|
|
|
|
|
|
return 0;
|
|
|
|
|
|
}
|
|
|
|
|
|
```
|