python/TangDou/AcWing/GraphDfs/846.md

##[$AcWing$ $846$. 树的重心](https://www.acwing.com/problem/content/848/)

### 一、题目描述
给定一颗树，树中包含 $n$ 个结点（编号 $1∼n$）和 $n−1$ 条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

**输入格式**
第一行包含整数 $n$，表示树的结点数。

接下来 $n−1$ 行，每行包含两个整数 $a$ 和 $b$，表示点 $a$ 和点 $b$ 之间存在一条边。

**输出格式**
输出一个整数 $m$，表示将重心删除后，剩余各个连通块中点数的最大值。

**数据范围**
$1≤n≤10^5$

**输入样例**
```cpp {.line-numbers}
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
```

**输出样例：**
```cpp {.line-numbers}
4
```

### 二、题意分析

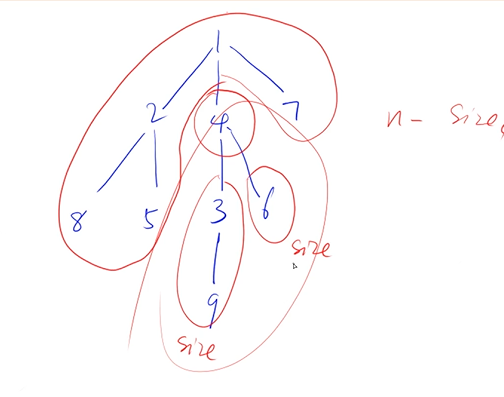
**1. 什么树重心？**
![](https://img2022.cnblogs.com/blog/8562/202203/8562-20220319160848457-421715650.png)


**重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。**

树的重心不一定只是一个，有时可以是两个。

**2. 如何求树的重心**
在树上可以进行两种遍历：深度、广度。其中深度遍历可以模拟一支笔在树上画线，直至遍历完成所有节点。我们可以利用这一特点，让每个大臣分派出任务时，都要求下一级的官员返回自己管辖范围内的结点数。然后它自己负责把下级返回的个数加在一起，再加上自己的结点数1，返回给上级调用者。


### 三、实现代码
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 100010, M = 200010;
const int INF = 0x3f3f3f3f;
int ans = INF;
bool st[N];
int n;
int h[N], e[M], ne[M], idx;
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int dfs(int u) {
    st[u] = 1;
    int sum = 1;
    int res = 0;
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (!st[v]) {
            int s = dfs(v);    // v子树有多少个节点
            sum += s;          // 儿子们的节点个数累加和,再加自己的1，就是u子树的节点个数sum和
            res = max(res, s); // 猴子选大王
        }
    }
    res = max(res, n - sum); // 套路:除了自己的所有猴子，还要考虑反向子树
    ans = min(ans, res);     // 最大中选最小，就是树的重心
    return sum;
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n;                     // n个顶点
    for (int i = 1; i < n; i++) { // n-1条边
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }
    dfs(1);
    cout << ans << endl;
    return 0;
}
```