python/TangDou/AcWing/Discretization/802.md

##[$AcWing$ $802$. 区间和 ](https://www.acwing.com/problem/content/804/)

### 一、题目描述
假定有一个无限长的数轴，数轴上每个坐标上的数都是 $0$。

现在，我们首先进行 $n$ 次操作，每次操作将某一位置 $x$ 上的数加 $c$。

接下来，进行 $m$ 次询问，每个询问包含两个整数 $l$ 和 $r$，你需要求出在**区间 $[l,r]$ 之间的所有数的和**。

**输入格式**
第一行包含两个整数 $n$ 和 $m$。

接下来 $n$ 行，每行包含两个整数 $x$ 和 $c$。

再接下来 $m$ 行，每行包含两个整数 $l$ 和 $r$。

**输出格式**
共 $m$ 行，每行输出一个询问中所求的区间内数字和。

**数据范围**
$−10^9≤x≤10^9$,
$1≤n,m≤10^5$,
$−10^9≤l≤r≤10^9$,
$−10000≤c≤10000$

**输入样例：**
```cpp {.line-numbers}
3 3
1 2
3 6
7 5
1 3
4 6
7 8
```

**输出样例：**
```cpp {.line-numbers}
8
0
5
```

![](https://img2020.cnblogs.com/blog/8562/202109/8562-20210908112555379-1412665004.png)

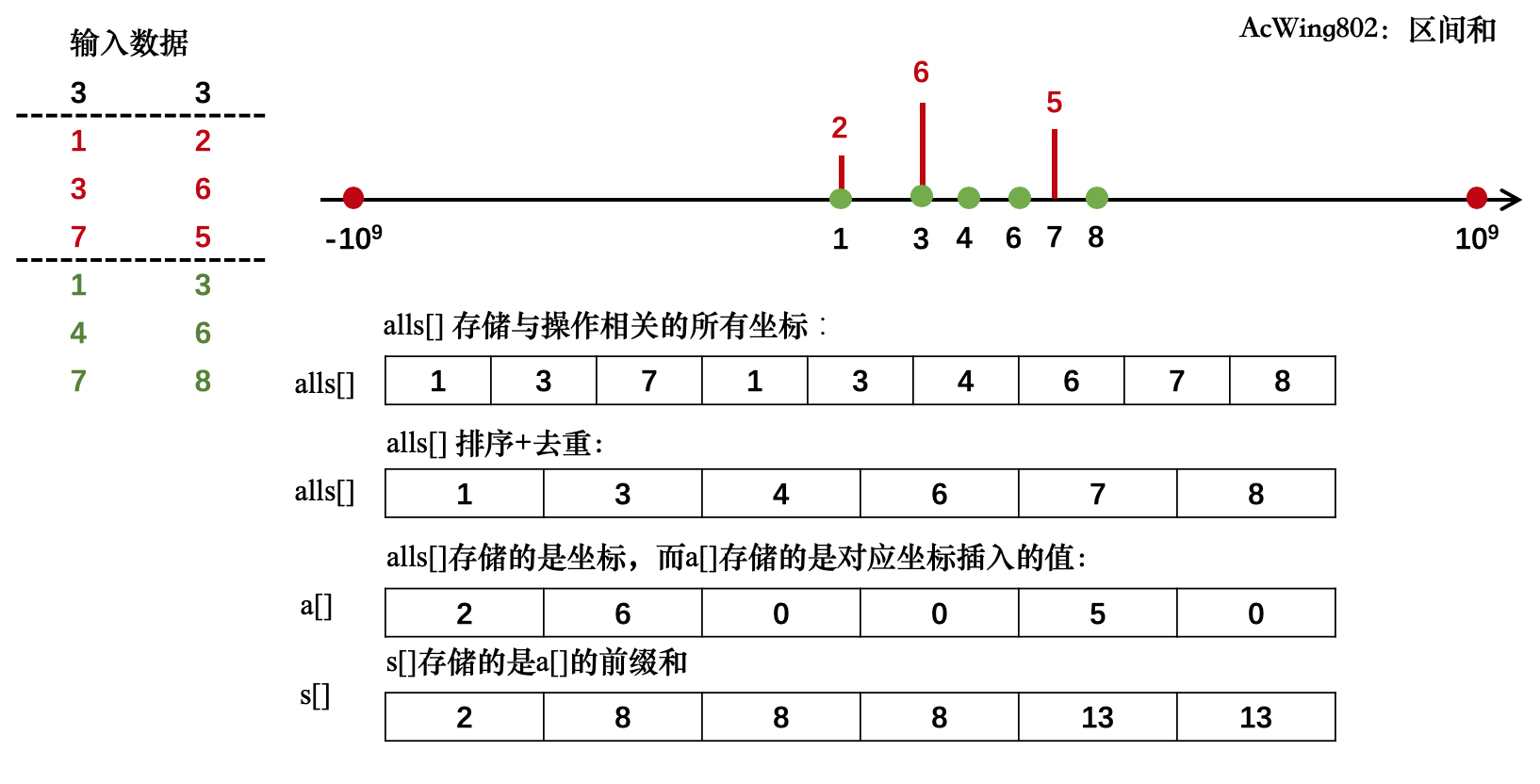
**特殊说明一下，$alls$数组下标是从$0$开始的，而$a$数组下标是从$1$开始的，$alls$数组与$a$数组是一一对应的，但是错位对应的，即$alls[0]->a[1],alls[1]->a[2],....$**

### 二、解题思路

1. **为什么要离散化**？
因为 **[空间上不允许开那么大数据范围的数组](https://www.cnblogs.com/littlehb/p/15304297.html)** ！本题$−{10}^9≤x≤10^9$,,两边都加上就是$2*10^9$,$c++$开不到$3e7$以上,空间超限。

2. **什么是离散化**？
**离散化**:范围大，但比较稀疏，真正有数的不多，很多地方是空着的（空着的是0）。利用这一特点，把有用的位置 **映射** 到一个长度可控的范围上。

3. **数组大小的确定**
既然要映射到一块小的、能装的下的区域内，那么这个区域最大是多大呢？
因为原始数据坐标共$n$个，而查询时坐标是$[l,r]$，一次两个，一共$m$次，需要把所有的坐标全部放到$a$数组中，上限是：$n+2*m$,依题意，就是$3*1e5$

4. **离散化模板**
```c++
// ① 排序+去重
sort(a, a + al);
// ② 使用STL的去重函数去重，不用手写的去重，原因：只排序一次，去重一次，不像是二分需要重复使用，性能差另不大，但代码就短的多
al = unique(a, a + al) - a;
```

### 三、模板代码
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
typedef pair<int, int> PII;

const int N = 300010;
int a[N], al;
int b[N], s[N]; // 假定有一个无限长的数轴，数轴上每个坐标上的数都是 0

PII q[N], p[N];
int ql, pl;

int n, m;

// 手写二分
int lower_bound(int q[], int l, int r, int x) {
    while (l < r) {
        int mid = (l + r) >> 1;
        if (q[mid] >= x)
            r = mid;
        else
            l = mid + 1;
    }
    return l;
}

int main() {
    cin >> n >> m;
    while (n--) {
        int x, c;
        cin >> x >> c;
        p[pl++] = {x, c};
        a[al++] = x;
    }

    int l, r;
    while (m--) {
        cin >> l >> r;
        q[ql++] = {l, r};
        a[al++] = l, a[al++] = r;
    }

    // ① 排序+去重
    sort(a, a + al);
    // ② 使用STL的去重函数去重，不用手写的去重，原因：只排序一次，去重一次，不像是二分需要重复使用，性能差别不大，但代码就短的多
    al = unique(a, a + al) - a;

    // 处理一下某个x上加c的事情
    for (int i = 0; i < pl; i++) {
        int x = lower_bound(a, 0, al, p[i].first) + 1; // 下标从0开始，需要加1个偏移量
        b[x] += p[i].second;
    }

    // 一维前缀和
    for (int i = 1; i < N; i++) s[i] = s[i - 1] + b[i];

    // 处理询问(前缀和应用)
    for (int i = 0; i < ql; i++) {
        // 根据原来的位置值，计算出映射后的位置值
        l = lower_bound(a, 0, al, q[i].first) + 1;
        r = lower_bound(a, 0, al, q[i].second) + 1;
        // 利用一维前缀和计算区间和
        printf("%d\n", s[r] - s[l - 1]);
    }
    return 0;
}
```
### 四、总结
- 提到的所有位置点，不管是有数值的点，还要是查询的点，统统记录到$a[]$数组中
- 对$a$数组进行排序+去重操作
- 遍历每一个有值的点，通过二分将原坐标变换为新的坐标，使用一个基础数组$b[]$,记录新坐标中对应的数值
- 对基础数组$b$生成前缀和数组$s[]$
- 利用前缀和数组$s[]$回答问题