python/TangDou/AcWing/BIT/241.md

##[$AcWing$ $241$ 楼兰图腾](https://www.acwing.com/problem/content/243/)

### 一、题目描述
在完成了分配任务之后，西部 $314$ 来到了楼兰古城的西部。

相传很久以前这片土地上(比楼兰古城还早)生活着两个部落，一个部落崇拜尖刀($V$)，一个部落崇拜铁锹($∧$)，他们分别用 $V$ 和 $∧$ 的形状来代表各自部落的图腾。

西部 $314$ 在楼兰古城的下面发现了一幅巨大的壁画，壁画上被标记出了 $n$ 个点，经测量发现这 $n$ 个点的水平位置和竖直位置是两两不同的。

西部 $314$ 认为这幅壁画所包含的信息与这 $n$ 个点的相对位置有关，因此不妨设坐标分别为 $(1,y_1),(2,y_2),…,(n,y_n)$，其中 $y_1∼y_n$ 是 $1$ 到 $n$ 的一个排列。

西部 $314$ 打算研究这幅壁画中包含着多少个图腾。

如果三个点 $(i,y_i),(j,y_j),(k,y_k)$ 满足 $1≤i<j<k≤n$ 且 $y_i>y_j,y_j<y_k$，则称这三个点构成 $V$ 图腾;

如果三个点 $(i,y_i),(j,y_j),(k,y_k)$ 满足 $1≤i<j<k≤n$ 且 $y_i<y_j,y_j>y_k$，则称这三个点构成 $∧$ 图腾;

西部 $314$ 想知道，这 $n$ 个点中两个部落图腾的数目。

因此，你需要编写一个程序来求出 $V$ 的个数和 $∧$ 的个数。

**输入格式**
第一行一个数 $n$。

第二行是 $n$ 个数，分别代表 $y_1，y_2,…,y_n$。

**输出格式**
两个数，中间用空格隔开，依次为 $V$ 的个数和 $∧$ 的个数。

**数据范围**
对于所有数据，$n≤200000$，且输出答案不会超过 $int64$。
$y_1∼y_n$ 是 $1$ 到 $n$ 的一个排列。

**输入样例**：
```cpp {.line-numbers}
5
1 5 3 2 4
```

**输出样例**：
```cpp {.line-numbers}
3 4
```
![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/{year}/{month}/{md5}.{extName}/202308150918512.png)

![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/{year}/{month}/{md5}.{extName}/202308150921994.png)

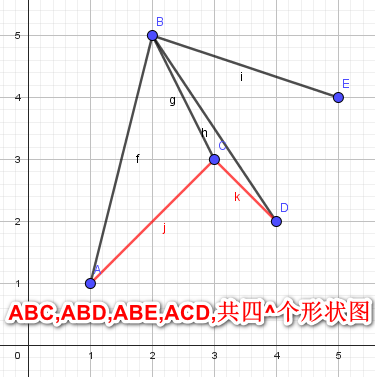
>**注**：$BCD$不是啊！一开始我以为$BCD$也是，后来才明白，那个$D$的$Y$轴坐标从$C$要小，这是不行的，需要对$C$的$Y$轴坐标大才对。

**规律**
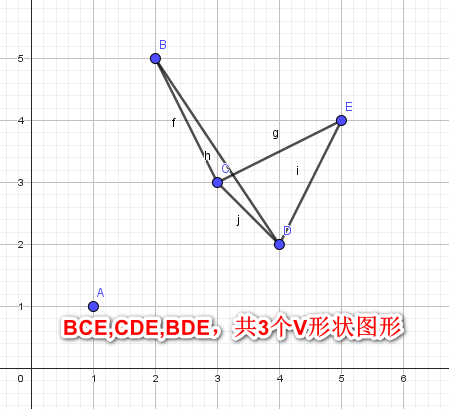
- $V$形状：对于任意点而言，需要找出左侧比我大的，乘以，右侧比我大的，然后累加这些乘积
- $∧$形状：对于任意点而言，需要找出左侧比我小的，乘以，右侧比我小的，然后累加这些乘积

### 二、暴力做法


这题的思路比较容易想到，想要知道某个点为底产生的正（倒）三角形有多少，只要知道该点左右两边比他大（小）的数的数量即可。如果某个点左边比他大的数有$a$个，右边比他大的有$b$个，则该点为底的倒三角就有$a * b$个。如果直接遍历的话每个数字都要找一遍，复杂度为$O(n^2)$。 $n≤200000$,$2e5*2e5=4e10$,$c++$一秒能计算$1e9$,肯定会超时。

```cpp {.line-numbers}
#include <bits/stdc++.h>
// 暴力大法好!
//  过掉4/10个数据
using namespace std;
const int N = 2000010;
typedef long long LL;

int a[N];
// ll[i]表示i的左边比第i个数小的数的个数
// rl[i]表示i的右边比第i个数小的数的个数
// lg[i]表示i的左边比第i个数大的数的个数
// rg[i]表示i的右边比第i个数大的数的个数
int ll[N], rl[N], lg[N], rg[N];

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]); // 纵坐标

    // 双重循环，暴力求每个坐标左边比自己小，比自己大的个数
    for (int i = 1; i <= n; i++)
        for (int j = 1; j < i; j++) {
            // a[]保存的是1 ~ n的一个排列，不可能相等(题意)
            if (a[j] < a[i])
                ll[i]++;
            else
                lg[i]++;
        }
    // 双重循环，暴力求每个坐标右边比自己小的，比自己大的个数
    for (int i = 1; i <= n; i++)
        for (int j = i + 1; j <= n; j++) {
            if (a[j] < a[i])
                rl[i]++;
            else
                rg[i]++;
        }
    // 利用乘法原理，计算左侧比自己小，右侧比自己小的数量乘积（或比自己大）
    LL resV = 0, resA = 0;
    for (int i = 1; i <= n; i++) {
        resV += (LL)lg[i] * rg[i];
        resA += (LL)ll[i] * rl[i];
    }
    printf("%lld %lld\n", resV, resA);
    return 0;
}
```
### 三、解题思路

首先，我们可以发现数的范围不大仅是只有$1$到$n$，最大不超过$2e5$,那么我们考虑是不是可以在处理每个数的时候，把这个数直接放进对应下标的数组中，然后直接求$a_i$到$n$有多少个数。那么我们就需要一个方法去达到快速修改数组中的一个数，并且能够快速求出前缀和。

那么，我们不难想到 **树状数组** (**线段树**) 可以用来处理这个问题。

* 对于$∧$我们只需要先从$1$到$n$求一遍比$a_i$小的值个数，然后再从$n$到$1$求一遍比$a_i$小的值个数，两者通过乘法原理乘在一起，就是 $∧$的个数。

* 题目还要求求一下$V$的个数，这个可以通过上面的求解过程中，采用逆向思维来一并求出：
我现在在$i$这个位置，值是$x=a[i]$,比我小的用树状数组求出来了前缀和，计为$sum(x-1)$,那么比我大的呢？就是$sum(n)-sum(x)$个。

![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/{year}/{month}/{md5}.{extName}/241.jpg)

### $Code$
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 200010;

int n, a[N];         // n个元素，a[i]代表原始值
LL big[N], small[N]; // big[i]:比a[i]大的元素个数，small[i]:比a[i]小的元素个数
LL res1, res2;       // V的个数，∧的个数

// 树状数组模板
#define lowbit(x) (x & -x)
int c[N];
void add(int x, int v) {
    while (x < N) c[x] += v, x += lowbit(x);
}
LL sum(int x) {
    LL res = 0;
    while (x) res += c[x], x -= lowbit(x);
    return res;
}

// 桶计数+前缀和
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i++) { // 枚举每个点，由左到右一个个下场
        int x = a[i];
        small[i] = sum(x - 1);        // 在我前面出场，并且，值比我小, 用于方便统计铁锹(∧)
        big[i] = sum(n) - sum(x - 1); // 在我前面出场，并且，值比我大, 用于方便统计尖刀(V)
        add(x, 1);                    // 以值为桶的标识，记录此桶中数量+1
    }

    memset(c, 0, sizeof c);

    for (int i = n; i; i--) {
        int x = a[i];
        res1 += small[i] * sum(x - 1);
        res2 += big[i] * (sum(n) - sum(x - 1));
        add(x, 1);
    }
    printf("%lld %lld\n", res2, res1);
    return 0;
}
```
### 四、总结
树状数组是一种用于快速计算前缀和的数据结构，它可以支持两种操作：修改和查询。

- 1. 多次修改后最终查询一次：这种情况适用于当我们知道需要对数组进行多次修改操作，但是只需在最后一次修改后进行查询。例如，在一个数组中，我们需要频繁地对某个元素进行增减操作，而在最后一次修改结束后，我们需要快速地查询某个区间的和。

- 2. 一边修改，一边查询：这种情况适用于需要频繁地对数组进行修改操作的同时，需要实时查询某个区间的和。例如，在一个动态变化的数组中，我们需要不断地对元素进行修改，并在每次修改后立即查询某个区间的和，以便进行实时的数据统计或计算。

总之，树状数组在这两种情况下都可以发挥作用，根据具体的应用场景和需求，选择对应的使用方式可以提高计算效率和减少时间复杂度。

当一棵树状数组用于多次修改后最终查询一次的情况时，可以考虑以下示例：

假设有一个长度为n的数组A，初始时数组所有元素为$0$。现在需要进行$m$次操作，每次操作要么将某个元素加上一个值，要么查询某个区间的和。最终需要进行一次查询，获取某个区间的和。

操作示例：
- 1. 初始化数组$A$为$[0, 0, 0, 0, 0]$
- 2. 将$A[2]$加上$3$，数组变为$[0, 0, 3, 0, 0]$
- 3. 将$A[4]$加上$2$，数组变为$[0, 0, 3, 0, 2]$
- 4. 将$A[1]$加上$5$，数组变为$[0, 5, 3, 0, 2]$
- 5. 查询数组$A$在区间$[2, 4]$的和，即$A[2] + A[3] + A[4] = 3 + 0 + 2 = 5$

在这个例子中，我们先对数组$A$进行多次修改操作，最终只需要一次查询操作来获取区间$[2, 4]$的和。

当一棵树状数组用于一边修改，一边查询的情况时，可以考虑以下示例：

假设有一个长度为$n$的数组$A$，初始时数组所有元素为$0$。现在需要进行$m$次操作，每次操作要么将某个元素加上一个值，要么查询某个区间的和。每次操作都需要实时查询某个区间的和。

操作示例：
- 1. 初始化数组$A$为$[0, 0, 0, 0, 0]$
- 2. 将$A[2]$加上$3$，查询数组$A$在区间$[1, 3]$的和，结果为$A[1] + A[2] + A[3] = 0 + 3 + 0 = 3$
- 3. 将$A[4]$加上$2$，查询数组$A$在区间$[2, 4]$的和，结果为$A[2] + A[3] + A[4] = 3 + 0 + 2 = 5$
- 4. 将$A[1]$加上$5$，查询数组$A$在区间$[1, 4]$的和，结果为$A[1] + A[2] + A[3] + A[4] = 5 + 3 + 0 + 2 = 10$

在这个例子中，我们每次对数组$A$进行修改操作后，都立即查询了一次特定区间的和，以便获取实时的结果。

上面两种场景都是树状数组可以发挥作用的，本题就是使用了第二种场景，每一次变化后，及时统计计算当前场景下的情况，才可以得到左侧比我小，左侧比我大的数据个数。